【路径计数模型】
【卡特兰数】
组合意义:从 \((0,0)\) 走到 \((n,n)\),每次向右或者向上,不严格越过对角线的方案数。
它也和长度为 \(2n\) 的合法括号序列个数相等。各种问题都可以转化为卡特兰数。
回忆一下卡特兰数的计算方法。利用了割补和映射。
首先,所有路径条数是 \(\binom{n+n}{n}\)。对于超越对角线的方案,我们取它第一个超越的点翻转上去,得到 \((-1,1)\) 走到 \((n,n)\) 的路径。所以超越对角线的条数与 \((-1,1)\) 到 \((n,n)\) 的路径条数相等。所以答案为 \(\binom{n+n}{n}-\binom{n+n}{n+1}\)。
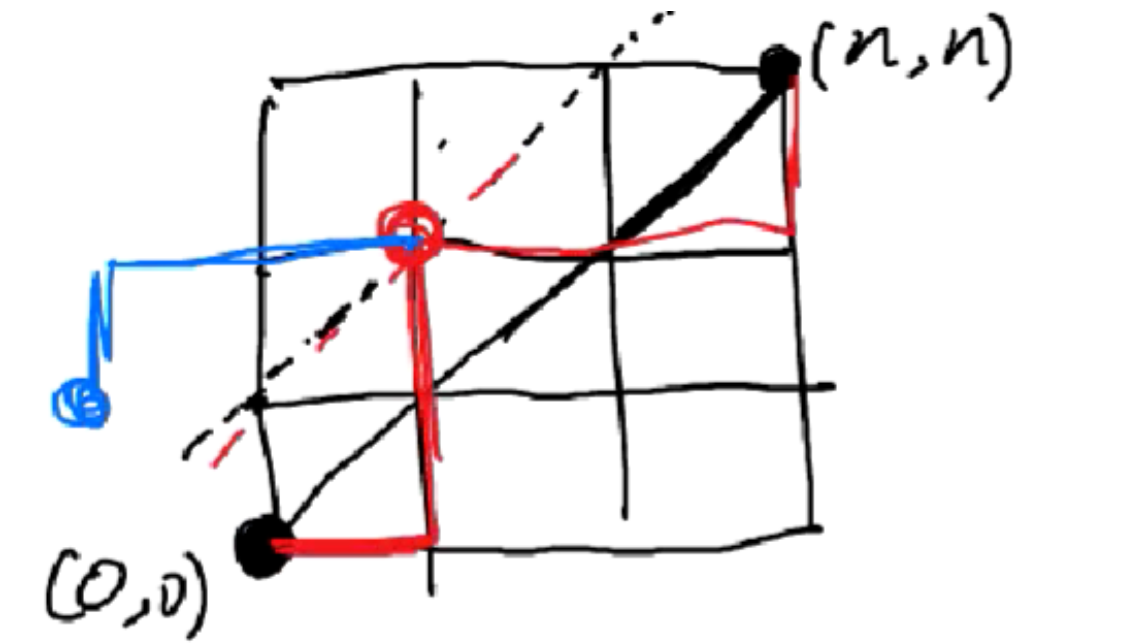
【路径计数拓展一】
作为卡特兰数扩展。从 \((0,0)\) 走到 \((n,m)\),不经过 \(y=x+b\),有多少条路径?
同理,把第一个碰到的之前都翻转过去。
改写为 \(x-y+b=0\)。
这里用到点到直线距离公式:\(\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)。
所以 \((0,0)\) 到 \(x-y+b=0\) 的距离就是 \(\dfrac{|b|}{\sqrt 2}\),设对称过去的点是 \((u,-u)\),则 \(\dfrac{|b|}{\sqrt 2}=\dfrac{|2u+b|}{\sqrt 2}\)。因为 \(b\) 是正数,所以 \(|2u+b|=b\),所以 \(u=-b\)。
因此,路径条数为 \(\binom{n+m}{n}-\binom{n+m}{n+b}\)。
【路径计数拓展二】
假设上下有两条线不能经过:\(y=x+b\) 和 \(y=x-a\)。也就是任何时刻 \(-a<y-x<b\)。记上面的线是 \(L\),下面的线是 \(R\)。
有很多方法解决这个问题。
【做法一】
给每条 \((0,0)\rightarrow (n,m)\) 的路径定义一个字符串标签,可能是空串、L、R、LR 交替类、RL 交替类。分别表示 "没有碰到"、"只碰到 L"、"只碰到 R"、"先碰到 L 再碰到 R ……" 和 "先碰到 R 再碰到 L ……"。
注意这个字符串不会有相邻的相同字符,也可以很长(在两条线之间来回碰)。
然后定义 \(f(s)\),\(s\) 是字符串。它表示标签含 \(s\) 为子串的路径个数。例如 \(f(\empty)=\binom{n+m}{n}\)。
以及 \(g(s)\),表示标签恰好为 \(s\) 的路径个数。答案就是 \(g(\empty)\)。
在计算 \(f\) 之前,我们先考虑怎么用 \(f\) 算答案:
这种容斥我们叫做反射容斥,也有的叫做前缀容斥。
然后考虑怎么求 \(f\)。\(f(\empty)\) 就是 \(\binom{n+m}{n}\)。
-
\(f(L)\),就是要求有碰到 \(L\) 的路径条数。反射过去之后容易得到条数。
-
\(f(R)\),与 \(f(L)\) 类似。
-
\(f(LR)\)。先把 \((0,0)\) 折到 \(L\) 的一侧得到点 \(O'\),然后再把 \(O'\) 折到 \(R\) 的一侧得到 \(O''\),求点 \(O''\) 到 \((n,m)\) 的路径条数即可。
-
\(f(RL)\) 类似。
-
\(f(LRL)\),先与 \(L\) 对称,再与 \(R\) 对称,再再与 \(L\) 对称。
-
以此类推 ……
化简后得到:
【应用】
进出栈问题
当只要求空时不允许出栈,答案就是卡特兰数。
当给栈加上容量限制,例如额外要求在栈里有 \(5\) 个数不允许入栈,等价于有两条线不允许碰。可以使用反射容斥解决。
LOJ6738 王的象棋世界(神题)
因篇幅过长,详情见 "题目分析/数学/LOJ6738 王的象棋世界"。
UOJ424 Count
经过一些转化后,题意为:求左拐度 \(<m\) 的 \(n\) 大小二叉树个数。
(本题在【OGF 学习笔记】里给出了一种不涉及反射容斥的解法)
这个问题乍一看和反射容斥没有关系,但我们可以做转化:\(n\) 结点二叉树与 \(2n\) 长度合法括号序列一一对应。
怎么映射呢?
对于一个二叉树结点 \(u\),若 \(u\) 为叶结点,\(f(u)=\) ();否则 \(f(u)=(f(L))+f(R)\)。
左拐度 \(<m\),即括号序列的嵌套层数 \(\le m\)。
而对于某个位置 \(i\),\(i\) 所在的嵌套层数就是 \(i\) 左侧的左括号减去右括号数。
所以问题转化为:\((0,0)\rightarrow (n,n)\),不碰到 \(y=x+1\) 和 \(x=y+(m+1)\) 的路径数。
使用反射容斥可以优雅地解决。
CF1821F Timber
在 \([1, n]\) 的区间里放 \(m\) 棵树,每棵树的高度为 \(k\)。求有多少种放置树的方法,满足:
- 每个树都在整点上,且每个点最多只能放一棵树。
- 存在一种砍倒树的方案,使得树倒了之后不会越界,也不会有某个点被超过一棵树占据。你可以自由选择树向左倒(也就是占据区间 \([x - k, x]\))或者向右倒(也就是占据区间 \([x, x + k]\))。
\(1\leq n, m, k\leq 3\times 10 ^ 5\)。
(介绍过母函数优化 DP 的解法)
先考虑如何判定是否存在合法的倒下方案,显然贪心地能向左倒就向左即可。
所以可以设计 \(dp[i][j]\) 为 \([1,i]\) 种了 \(j\) 棵树的方案数。
(因为当 \(t\) 太大的时候,根据我们尽量向左的要求,只能向左倒不能向右倒,故只乘 \(1\))
怎么转化为路径计数呢?
把这个转移方程里 \(i\) 看作行,\(j\) 看作列。从 \((i,j)\) 走到 \((i+1\sim 2k,j+1)\) 边权 \(2\),走到 \((i+2k+1\sim inf,j+1)\) 边权 \(1\)。求 \((0,0)\rightarrow (1\sim n,m)\) 所有路径权值和,权值定义为经过的边权乘积。
把图改造一下,原本是:

改造成:
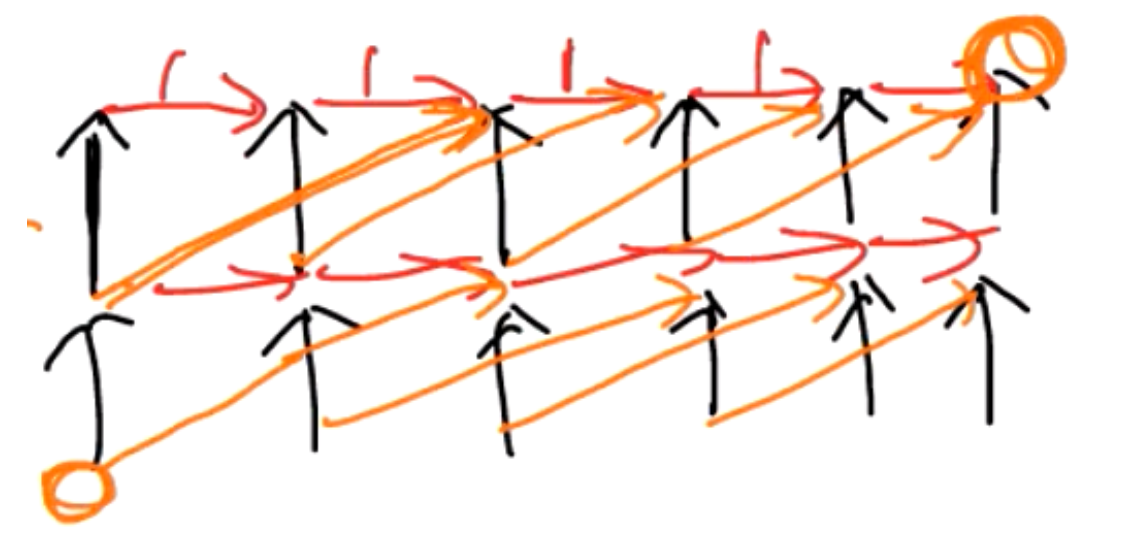
黑边权值 \(2\),其他权值 \(1\)。
这个路径计数,只需要枚举选择了几条黄色边即可,可以线性求出。
【Raney Lemma】
卡特兰数问题,除了使用折线法,还可以使用 Ramey Lemma 解决;将这个做法推广之后可以得到一些很有意思的结论。
考虑 \(H=(h_1,\cdots,h_L)\),\(\sum h_i=1\)。有结论:在 \(H\) 所有 cyclic-shift 中,"前缀和为正的位置个数" 恰好为 \(1\sim L\)。
来考虑一下和卡特兰数的关系。卡特兰数等价于 \(n+1\) 个 \(1\),\(n\) 个 \(-1\),前缀和都为正数。
(因为前缀和都为正数,\(h_1\) 必为 \(1\),之后就是 \(n\) 个 \(\pm 1\))
排列总个数是 \(\binom{2n+1}{n}\),把每一个排列的 cyclic-shift 分为一组,一组恰有一个是有效的。所以答案为 \(\dfrac{\binom{2n+1}{n}}{2n+1}\)。
再考虑和括号序列的关系。
问题:\(n\) 个
(和),定义 \(cnt(p)\)(\(p\) 为一个括号序列),表示 \(p\) 内有多少个 \(i\) 满足第 \(i\) 个)在第 \(i\) 个(之前。
显然 \(cnt(p)=0\iff p\) 合法。
结论:在 \(\binom{2n}{n}\) 个排列里,\(cnt(p)=0,1,2,\dots\) 的排列个数都有 \(\dfrac{\binom{2n}{n}}{n+1}\),即 \(cnt(p)\) 是等概率分布的。


)
-Agent、BaseAgent、ReactAgent 分析)


 – Reliable Replacement)





计算器实现 - 指南)






)