看到一篇公众号文章《2020年什么编程语言最受欢迎，待遇最高？》，其中对C#的描述如下：

点击阅读原文，看到这是一篇翻译文章：https://codinginfinite.com/top-programming-languages-2020-stats-surveys/

这篇文章里列出的那些语言之中，明显的Go 是属于Google 这个特定供应商的语言， Java 也是属于Oracle 这个特定供应商的语言。但是在文章中并没有这么说它们，而尽是美妙之言。对C# 就非常的刻薄，完全置事实于不顾。

我们先来看下Java：

2006年11月13日，Sun Microsystems正式宣布Java开源，并希望此举能够让社区帮助进行安全分析、bug报告、增强性能、了解偏僻个案等。
不过，十年过去之后，对于Java开源的争议依旧存在。批评者认为，Java并没有像官方说的那样完全开源，其实只开放了SDK，而Java SE和Java EE TCKs仍然是闭源的。
对于Java的开源身世，最初IBM呼吁将Java捐给Apache 软件基金会，使用Apache许可证分发，但Sun最终决定在GPL许可证下开源Java。GPL许可证要求衍生版本需要公开分发。Gosling称这能让Java更好的适应开源社区。Sun在2010年被甲骨文收购，Java也落到了甲骨文手中，由甲骨文主导Java的演化，（ 引用自https://www.oschina.net/news/79031/is-java-opensource）。2019年1月起Oracle 对JDK 8+ 收费，各大云厂商出现了分裂的OpenJdk 发行版。

从这份资料里面我得到了以下两点：

1. Sun公司确实宣布开源了，但没有完全开源。

2. Sun公司在GPL许可证下开源java。

3. Oracle公司对JDK进行了收费。

我们再来看下Go：

Go已经成为云原生应用开发领域的霸主，开源也有好多年了，但是我去看了github上面 Go的开源协议不是我们熟知的类型：https://github.com/golang/go/blob/master/LICENSE。Go的控制权属于google。

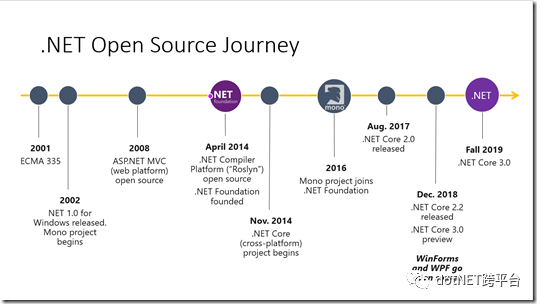
C# 是属于.NET基金会下面的开源项目，它才真正是不属于特定供应商的语言。为什么这么说，我就得给大家介绍一下.NET基金会。.NET基金会是一个独立的组织，支持.NET社区和开源，旨在拓宽和加强.NET生态系统和社区。这可以通过多种方式完成，包括项目指导，指导，法律和营销帮助，技术和财务支持设置等，2014年微软组织成立.NET基金会，微软在成为主要的开源参与者的道路上又前进了一步。2014年以来已经有众多知名公司加入.NET基金会, 仅在平台项目中，.NET平台上有87％贡献者其实不在Microsoft工作。2014年 .NET基金会的创始成员中有六位创始人，均非微软公司员工，随着微软的收购动作，Miguel 也成了微软员工，Migel一直在努力让.NET基金会独立于微软。.NET基金会改选结果参见https://dotnetfoundation.org/blog/2019/03/28，微软的Scott Hunter和migueldeicaza都没有竞选董事会，董事会中的只有一个微软员工Beth Massi，六位新任董事加入：Iris Classon， Ben Adams， Jon Skeet， Phil Haack， Sara Chipps 和Oren Novotny，仔细看了一下这些新加入成员的资料，多为MVP，具备社区影响力的同学。将.NET基金会变成一个更加多样化和成员驱动的组织，微软把.NET 的发展真正交给社区，为了让OSS真正蓬勃发展. 正所谓一图胜千言，我下面贴几张图来说明。

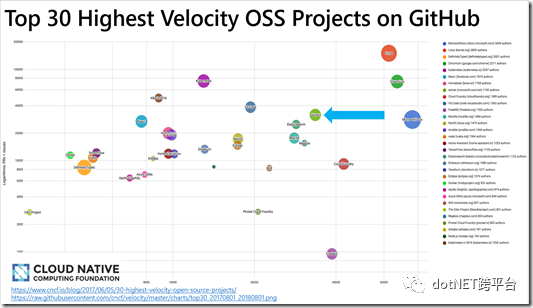
这张图参见 CNCF的博客 https://www.cncf.io/blog/2017/06/05/30-highest-velocity-open-source-projects/， .NET Core是唯一一个Github 上Top 30的开发平台。

以前.NET确实是微软的一部分，现在微软是.NET基金会的一部分

最后预告一下dotnet 峰会将在一个月后召开，会上将正式发布.NET Core 3.0：

原文链接：https://www.cnblogs.com/shanyou/p/11391726.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com