接下来我们就要慢慢步入在.NET Core中使用Docker的殿堂了，如题在开始之前，我们需要搞清楚一些概念，要不然看到官方提供如下一系列镜像，我们会一脸懵逼，不知道到底要使用哪一个。

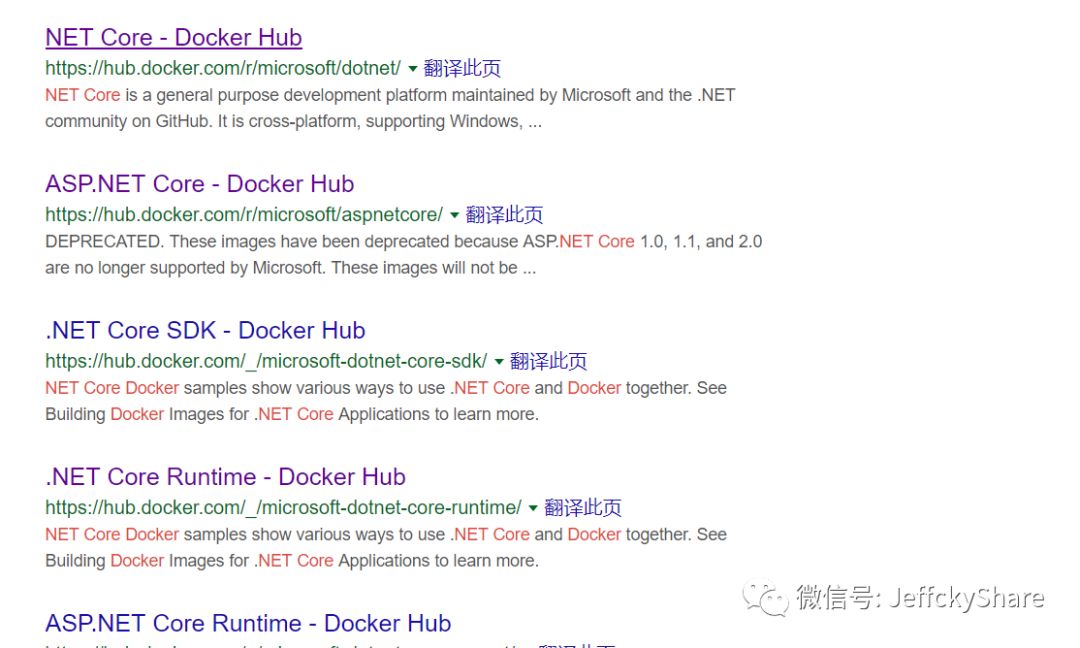
AspNetCore Runtime  VS .NetCore Runtime VS .NET Core SDK 

本节我们所讲解的官方所提供的一系列镜像都是最新镜像，而且阅读本文的您还需明白一点，要是您看到其他博文中提供的镜像以microsoft开头，那么说明已过时不再可取。

这里额外再多说一句，很多时候我们看到一些资料，然后亲自实践却没达到文章中所描述的效果，大部分情况下可能都是官方已更新导致，一切以官方文档为主才是最佳。我们将官方所提供的镜像作如下说明：

镜像地址	镜像名称	镜像说明
mcr.microsoft.com/dotnet/core/runtime	.NET Core Runtime	部署.NET Core控制台程序
mcr.microsoft.com/dotnet/core/runtime-deps	.NET Core Runtime Dependencies	部署自包含的部署应用程序
mcr.microsoft.com/dotnet/core/sdk	.NET Core SDK	构建.NET Core（或ASP.NET Core应用程序）
mcr.microsoft.com/dotnet/core/aspnet	ASP.NET Core Runtime	部署ASP.NET Core应用程序

上述对于.NET Core Runtime Dependencies镜像包我没做过多了解，在官方文档上有对这个的详细介绍名叫《SCD》，送上地址《https://docs.microsoft.com/en-gb/dotnet/core/deploying/index#self-contained-deployments-scd》，搞那么多包，好像很复杂似的，其实我们只需谨记如下两点

若需构建.NET Core应用程序，请使用.NET Core SDK

若需运行.NET Core应用程序，请使用.NET Core Runtime

比如上一节我们构建、发布应用程序直接在本地进行，所以我们只构建了.NET Core Runtime镜像，若在镜像中发布则还需提前下载.NET Core SDK镜像，接下来我们运行webapi来说明通过SDK镜像来构建程序，Runtime来运行程序。

这里需要注意下，若下载了3.0预览版本直接运行如下命令所创建的程序版本为3.0，此时可能会因缺少对应包而还原失败，所以这里我们将通过如下命令回退到2.2稳定版，继续往下走。

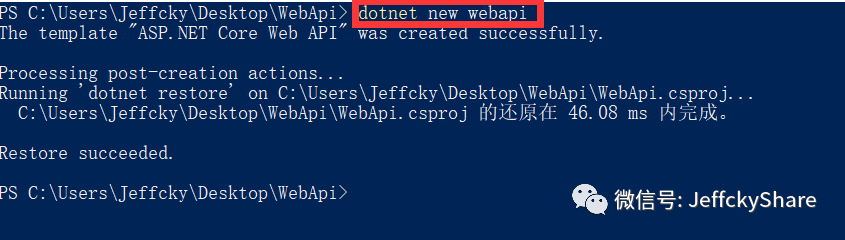
到这里为止我们并未如上一节那样直接发布，我们将其直接拖到ubuntu中，如下：

这里针对上一节内容补充说一句(个人有强迫症，上一节创建的镜像名称为(hellowrold)，这个镜像所打的标签单词名称打错了，应该是helloworld，所以这里我们重命名下镜像标签名称。又掌握了一个命令，哈哈。首先，我们查看镜像，如下

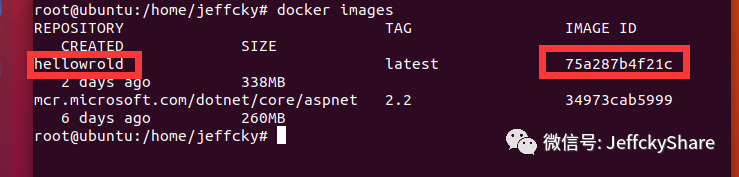
在Docker中重命名镜像标签名称有两种方式，一是直接通过标签名称来重命名，而是通过镜像id来重命名，如下：

我们通过如上任何一种方式重命名后再查看镜像，如下：

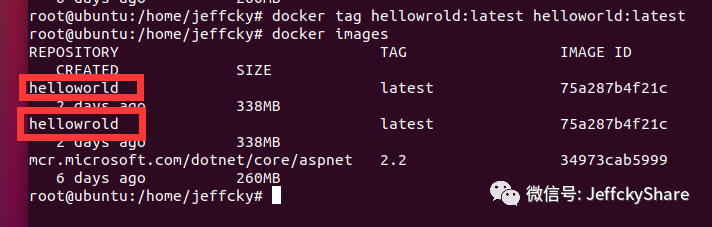
因为容器存在对旧镜像的引用，所以旧的会仍然存在而不是以新的进行完全覆盖，所以我们接下来执行如下命令将旧的镜像给移除：

通过执行如上命令会删除别名/标签，由于75a287b4f21c具有其他名称，因此不会删除实际图像。

回到正题，接下来我们开始通过Dockerfile来构建webapi镜像，如下：

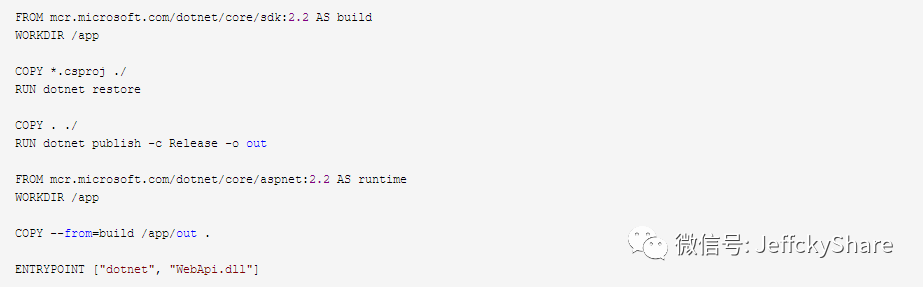
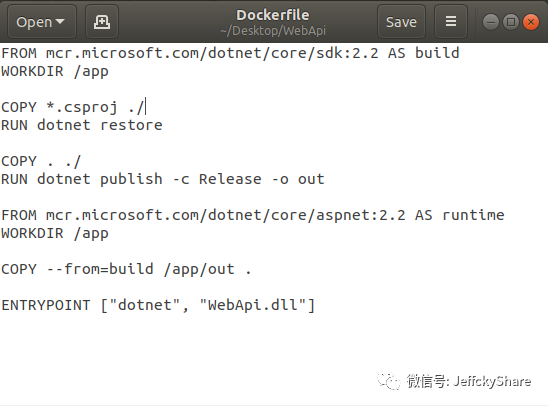
首先我们构建基础镜像SDK来构建应用程序，我们指定/app作为我们构建的工作目录。然后将文件从本地文件系统复制到镜像中，我们将只复制csproj文件并运行restore，然后复制其他剩余文件并运行dotnet publish来构建我们的应用程序并发布。

该文件的运行时部分使用不同的docker基础映像也就是使用aspnetcore-runtime映像，它复制构建中的所有文件，然后定义应用程序入口点。我们发现在整个构建镜像过程的不同阶段都是可交互的，因为如上我们第一阶段获取构建程序镜像也就是别名为build，在第二阶段获取运行程序镜像也就是runtime，我们引用了build。

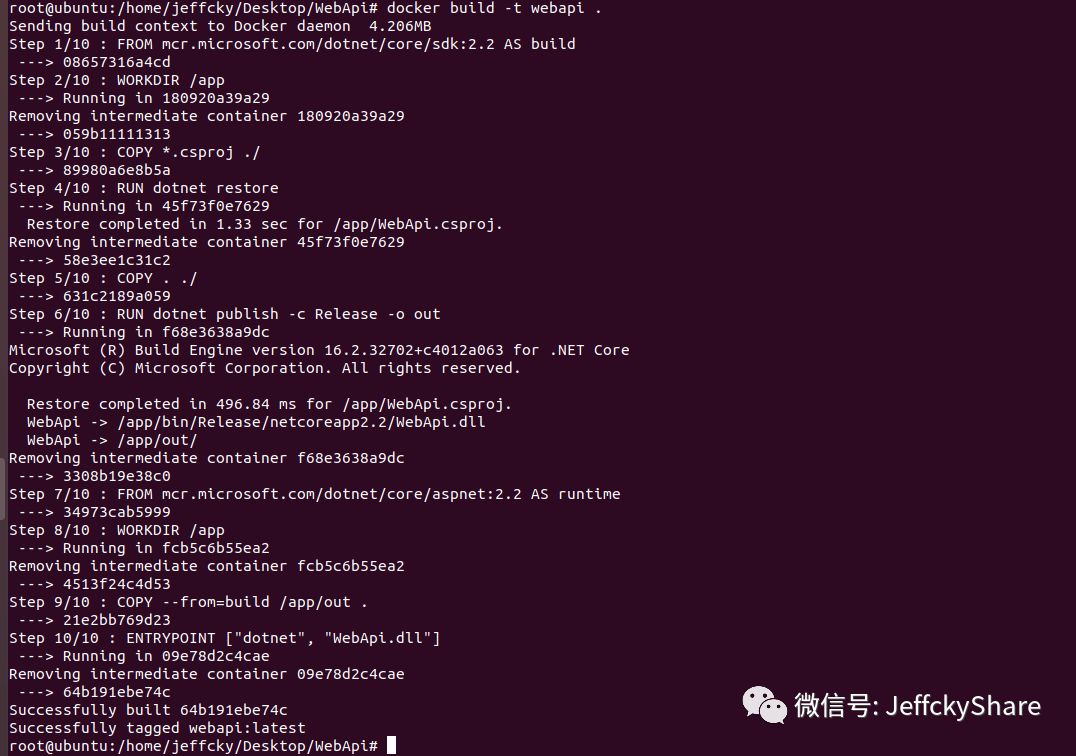
从如上我们构建镜像命令和上一节对比知道，构建命令可以通过如下两种方式来进行皆可。

构建镜像就是基于上一镜像层并创建一个新的镜像层的过程，每个新的镜像层都对应一个唯一的标识id，我们可以通过如下命令来查看镜像构建的历史记录：

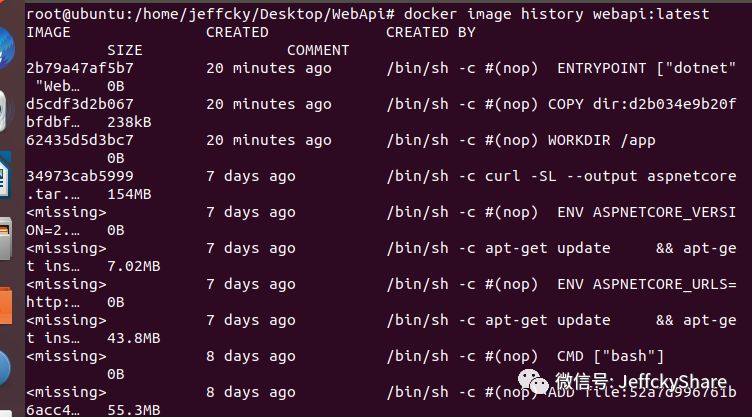
镜像“《none》”说明

当我们构建完镜像后，我们查看镜像列表会看到此时会多出了镜像标签名称为none的，如下：

如上生成的镜像none的作用是什么呢？我们是不是可以将其删除呢？

优点：它用来维护中间镜像层，因为对于每个Dockerfile说明的每一步骤，都会为中间层创建一个新的哈希值，通过允许缓存每个步骤来提高可重用性，减少磁盘使用量并加速docker构建。

缺点：它作为悬空镜像，可能会导致磁盘空间问题，但是它被列为docker镜像的一部分。（Docker中空的文件系统层是未使用的，并且没有被任何镜像所引用，因此我们需要一种机制让Docker清除这些空的镜像）

none的镜像只是为临时容器保存而已，由于Docker的架构，即使容器停止了，这些悬空的镜像也依然会保留，所以我们可以对其进行清理，我们可以使用docker rmi $(docker images -f "dangling=true" -q)来清理它们，-f "dangling = true" -q显示所有悬空镜像，rmi将删除所有这些图像。

若没有任何悬空镜像但执行了此命令，则会返回错误，但是我们可以使用docker images prune -a（仅适用于1.25以上的docker版本）。

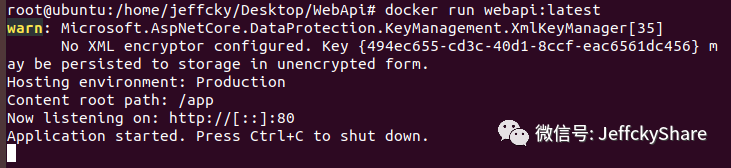
接下来则是创建并启动容器运行程序，上一节我们在代码中配置了端口号为5000，并且也通docker run -p 5050:5050 hellowrold 指定相同端口号运行程序，这里我们在代码中并未配置端口，所以默认端口号为80，如下：

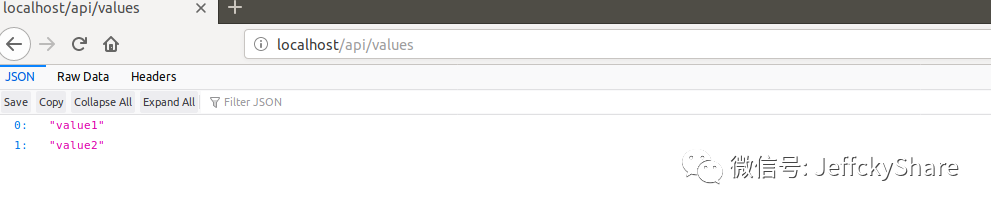
接下来如果我们访问http:// localhost/api/values，我们会看到无法连接，也就是说没有得到我们所期望的JSON响应。

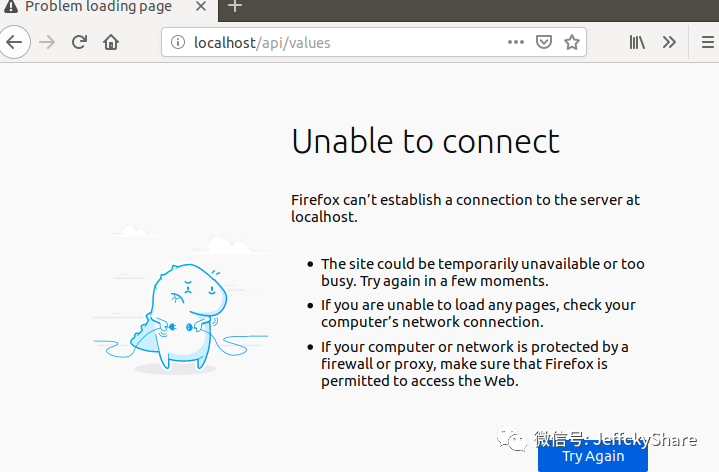
这是为何呢？我们来看看docker给我们生成容器的名称，docker给容器随机生成例如如下一个名称：

接下来我们通过终端运行容器管理命令来修复，我们首先将容器停止，然后进行移除，命令如下：

我们需要将gracious_chaplygi替换为从docker container ls返回的容器名称，我们使用以下命令再次启动容器：

如上我们配置了3个参数，--name是容器启动和运行时的名称，--env允许我们将环境变量传递给正在运行的容器，-p允许我们将容器上的端口映射到在我们的机器上的端口。

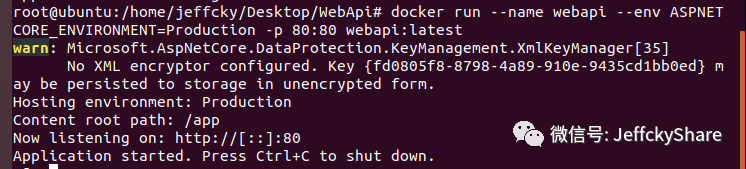
如上容器已启动，我们再次使用ls命令查看我们提供的名称和端口映射：

上述我猜测可能是因为容器名称随机生成的问题，然后指定了容器名称，结果好使了，但是上述我们再次获取容器名称时发现依然是随机生成的容器名称，所以我认为不是这个问题导致，

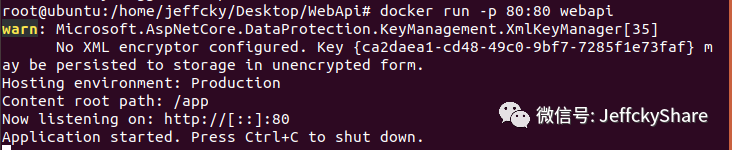
和上一节我们运行容器做本节对比，只是指定了映射端口号，而本节未指定端口号，默认启动端口号为80，容器也运行起来了呀，最终发现还是未指定端口号的缘故，因为当我启动容器时，也如下明确指定端口号为80就好使了，所以这里需要注意下。

本节我们讲解了在Docker中安装对应.NET Core镜像包的问题，并且以一个例子来说明，同时呢，我们在上一节使用指令的基础上又额外添加了对WORKDIR和RUN指令的使用，以及对容器停止、移除、镜像列表查看、镜像重命名、镜像删除、镜像构建历史记录查看指令的使用。接下来我们会继续通过例子来灵活使用各种指令，然后在这个过程中还涉及到一些可优化、以及Docker中比如卷、网络更深入的讲解。