散列之再散列

【0】README

0.1）本文描述总结于数据结构与算法分析，但源代码为原创；
0.2）为什么写这篇博文？再散列的代码实现包括了解决冲突的方法实现；很有代表性；（本源代码采用的解决冲突方法是平方探测法）

【1】问题+解决方法

1.0）开放定址法定义：它是一种不用链接解决冲突的方法：如果有冲突发生，那么就要尝试选择另外的单元，知道找出空的单元为止；
这里写图片描述
1.1）出现的问题：对于使用平方探测的开放定址散列法，如果表的元素填的太满，那么操作的运行时间将开始消耗过长，且 insert 操作可能失败，这可能发生在有太多的移动和插入混合的场合；
1.2）解决方法：建立另外一个大约两倍大的表（使用一个相关的新散列函数），扫描整个原始散列表，计算每个元素的新散列值并将其插入到新表中；
1.3）看个荔枝：

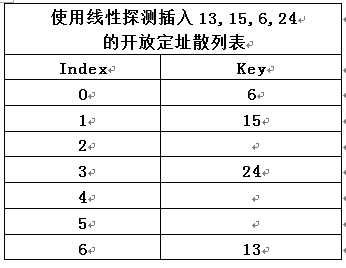
1）将元素13， 15， 24 和 6 插入到大小为 7 的开放定址散列表中：散列函数是 h（X） = X mod 7；设使用线性探测方法解决冲突问题，插入结果得到的散列表表示在下图中：
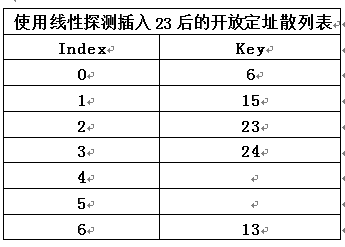
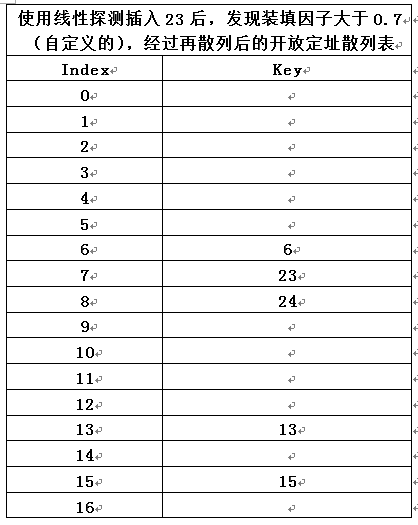
2）如果将 23 插入表中，那么从下图可以看到，插入后的表将有超过70% 的单元是满的，因为表填得过满，所以我们建立一个新表；该表的大小为 17，因为17是原表大小两倍后的第一个素数；新的散列函数为 h(X) = X mod 17；扫描原来的表，并将元素 6, 15, 23 , 24 以及13 插入到新表中，如下下图所示：

【2】再散列

2.1）定义：以上整个操作就叫做再散列；显然这是一种非常昂贵的操作，其运行时间为 O(N)，因为有N 个元素要再散列而表的大小约为2N，不过由于不是经常发生，所以实际效果根本不是那么差；
2.2）再散列的实现：
再散列可以用平方探测以多种方法实现：

1）一种做法是：只要表满到一半就再散列；
2）另一个极端方法是：只有当插入失败时才再散列；
3）第3种方法即途中策略：当表到达某一个装填因子时进行再散列。由于随着装填因子的增加，表的性能有所下降，因此，以好的截止手段实现的第三种策略，可能是最好的策略；

2.3）再散列的作用：
再散列就是把程序员从表大小的担心中解放出来，这一点很重要，因为在复杂的程序中散列表不能够做得任意地大；

【3】源代码+打印结果

3.1）解决冲突的方法：我们采用的是平方探测，1,-1,4,-4,……
3.2）Attention）在 “再散列”的代码中，我们为 HashTable 添加另一个 capacity 成员，用于和 size 相除构成装填因子，以便于判断该装填因子是否超出某个值；
3.3）downlaod source code : https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter5/p123_rehash.c
3.4）source code at a glance :

#include <stdio.h>
#include <malloc.h>
#include <math.h>#define ElementType int
#define Error(str) printf("\n error: %s \n",str)   struct HashTable;
typedef struct HashTable *HashTable;
struct HashEntry;
typedef struct HashEntry *HashEntry;
typedef HashEntry EntryArray;HashTable initHashTable(int size);
int find(ElementType key, HashTable ht);
HashTable insert(ElementType key, HashTable ht);enum EntryType {Legitimate, Empty, Deleted};struct HashEntry
{ElementType key;enum EntryType status;
};struct HashTable
{EntryArray entryArray;int capacity;int size;
};//judge whether the value is prime or not, also 1  or 0
int isPrime(int value)
{int temp;int flag;flag = 1;temp = 2;while(temp < sqrt(value)){if(value % temp == 0)flag = 0;temp++;}return flag;
}// compute the minial prime greater than the value
int nextPrime(int value)
{               value++;while(1){if(isPrime(value))break;value++;}return value;
} // hash function
int hashFunc(int key, int capacity)
{return key % capacity;
}// the rehash function to expand hash table capacity upto twice capcity
HashTable rehashFunc(HashTable ht)
{int capacity;int oldCapacity;int i;EntryArray temp;temp = ht->entryArray;oldCapacity = ht->capacity;capacity = nextPrime(ht->capacity * 2);ht = initHashTable(capacity);for(i = 0; i < oldCapacity; i++)if(temp[i].status == Legitimate)insert(temp[i].key, ht);free(temp);return ht;
}// initializing HashTable with given size and the table size should be a prime number
HashTable initHashTable(int capacity)
{HashTable ht;   int i;ht = (HashTable)malloc(sizeof(struct HashTable)); // allocate memory for HashTableif(!ht) {Error("out of space, from func initHashTable");return NULL;}ht->capacity = capacity; // the table capacity should be a prime numberht->size = 0; // the number the hash table stores elementht->entryArray = (HashEntry)malloc(capacity * sizeof(struct HashEntry)); // allocate memory for entry arrayfor(i = 0; i < capacity; i++) ht->entryArray[i].status = Empty;return ht;
}// insert the entry with value key into the Hash Table
HashTable insert(ElementType key, HashTable ht)
{int index;double loadFactor = 0.7; // let the load facotr equals to 0.7, of cource load factor depends on your minddouble temp;index = find(key, ht);if(ht->entryArray[index].status != Legitimate){ht->entryArray[index].status = Legitimate;ht->entryArray[index].key = key;ht->size++;// judge whether the load facotr is greater than the certain valuetemp = (double) ht->size / ht->capacity;        if(temp >= loadFactor)ht = rehashFunc(ht);}return ht;
}// find the index the entry with key should be placed into 
int find(ElementType key, HashTable ht) // find the hash entry with value key 
{int index;  int collisionIndex; int minus = -1;int temp;collisionIndex = 0;index = hashFunc(key, ht->capacity); // call the first hash function for allocating empty position for storing the key  temp = index;while(ht->entryArray[temp].status != Empty && ht->entryArray[temp].key != key ) // adopting square probing{if(minus == -1)collisionIndex++;minus *= -1;temp = collisionIndex * collisionIndex * minus;         temp = (index + temp) % ht->capacity;}       return temp;
}void printHashTable(HashTable ht)
{ElementType key;int i;  if(!ht)Error("printing execution failure, for hashtable is null, from func printHashTable");   i = 0;while(i < ht->capacity) {printf("\n\t index[%d] = ", i);key = ht->entryArray[i].key;    if(ht->entryArray[i].status == Legitimate)printf("%d", key);          elseprintf("NULL");printf("  ");       i++;}printf("\n\n");
}int main()
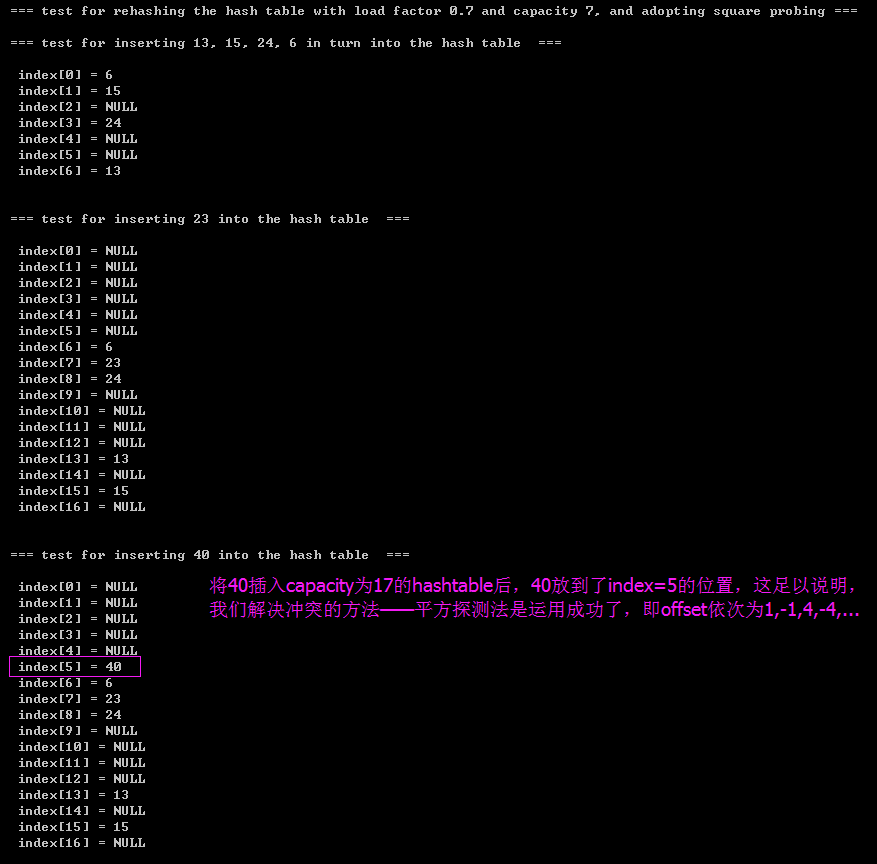
{HashTable ht = NULL;int dataSize = 4;int i;ElementType key[] = {13, 15, 24, 6};printf("\n\t=== test for rehashing the hash table with load factor 0.7 and capacity 7, and adopting square probing ===\n");ht = initHashTable(7);// the size of HashTable must be prime number;printf("\n\t=== test for inserting 13, 15, 24, 6 in turn into the hash table  ===\n");for(i = 0; i< dataSize; i++)    ht = insert(key[i], ht);    printHashTable(ht);     printf("\n\t=== test for inserting 23 into the hash table  ===\n");ht = insert(23, ht);    printHashTable(ht);     printf("\n\t=== test for inserting 40 into the hash table  ===\n");ht = insert(40, ht);    printHashTable(ht);     return 0;
}