垫场AA：深度：从 Office 365 新图标来看微软背后的设计新理念

--------------------------------------------------

前期01：尝试：Script Lab，快速 Office 365 开发工具

前期02：尝试：Script Lab，知识储备

前期03：实践：Script Lab，启动函数，Excel 基础操作（1）

前期04：实践：Script Lab，九九乘法表，Excel 基础操作（2）

前期04：Script Lab ，Office JavaScript API助手，Excel 基础操作（3）

前期06：Script Lab ，事件处理，Excel 基础操作（4）

前期07：Script Lab，单词“卡拉OK”，Word 基础操作

前期08：Script Lab，异步调用函数，PowerPoint 基础操作

--------------------------------------------------

垫场BB：为 Officejs 开发配置 VSCode 环境

准备

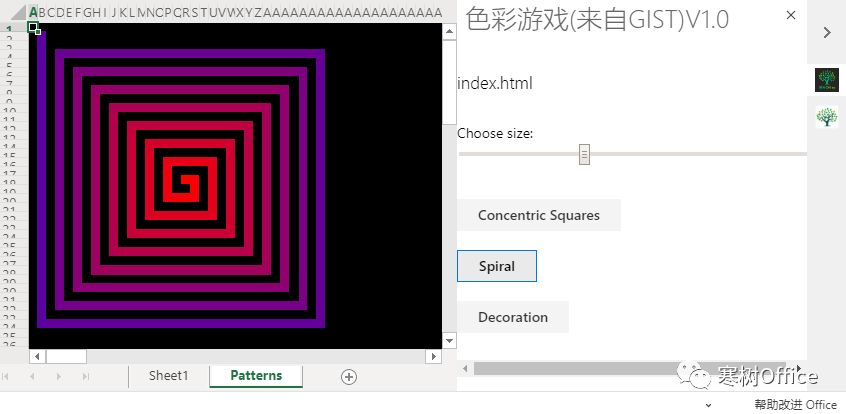
Script Lab 初级程教程己经靠一段落，前后共了8篇，作为 OfficeJS 开发入门己经缀缀有余。假设你使用Script Lab 创建了一个加载项的片段，那么你一定想把它变成一个一个独立的加载项。经过反复的偿试，还真找到一个最佳方法，可以轻松将代码片段转换为 OfficeJS 加载项。接着我们将进入第二阶段，向正式的 Web Add-ins 开发进军。

今天的内容将涉及大量的实操和安装过程，基本上是照着流程一步步来完成，半以一个最简单的 Script Lab 示例来操作，来最终完成一个 Web Add-ins 插件。

工具

这次我们将使用 VSCode 而不是 VS 来开发OfficeJS（Office 365 Web Add-ins）。VSCode  是一个非常有用的轻量级的代码编辑工具（就是这两天，许豪同志还在筹备相关的教程或专场）。除此之外，还需要两个辅助的工具，第一个是 Node Package Manager（NPM），和 Git 工具。通过 NPM 还将安装 Yoeman ，通过 yo 与 Git 等工具的配合，我们也将拥有一个令人惊讶的强大开发环境，说实话回到字符界面，就像回到 90 年代还在玩 DOS 的过程，“握控一切”的感觉实在是太好了（用了 VS 就不俱备了）。

【VSCode】

下载并安装VSCode，网址如下：

https：//code.visualstudio.com/

【nodejs】

下载并安装Node以获取节点包管理器（NPM），网址如下：

https：//nodejs.org/en/download/

【Git】

下载并安装Git，网址如下：

https：//git-scm.com/download

Yeoman

【CNPM 】

三大基础工具装好后，接着就是开始着 Yeoman 的安装了。之前的安装过程还都有顺利，但是到了这个环节时，还是遇到了一些小小的麻烦。网速问题导致晚上无法更新完成。临近11：30了，还没有见到安装完成的希望。今天这篇公众号文章，看样子是没办法完整的发出了，自打1月22日开号以来，可能是第一次断更的情况了。求助万能的大牛群 dotnet跨平台(飞雪)交流群，果然得到了答案，方知在国内该使用 cnpm 才对，并且得到了正确的命令（感谢 玮仔Wayne 的指导）。

我们现在需要做的是安装 CNPM，按以下流程操作：

1. 打开VSCode

2. 按CTRL +`。这将打开控制台窗口。或者，您可以转到“视图”菜单，然后单击“集成终端”

3. 切换到控制台中的终端，然后键入以下命令：

npm install -g cnpm --registry=https://registry.npm.taobao.org

【Yeoman】

yeoman 是 Google 的团队和外部贡献者团队合作开发的，他的目标是通过 Grunt（一个用于开发任务自动化的命令行工具）和 Bower（一个HTML、CSS、Javascript和图片等前端资源的包管理器）的包装为开发者创建一个易用的工作流。

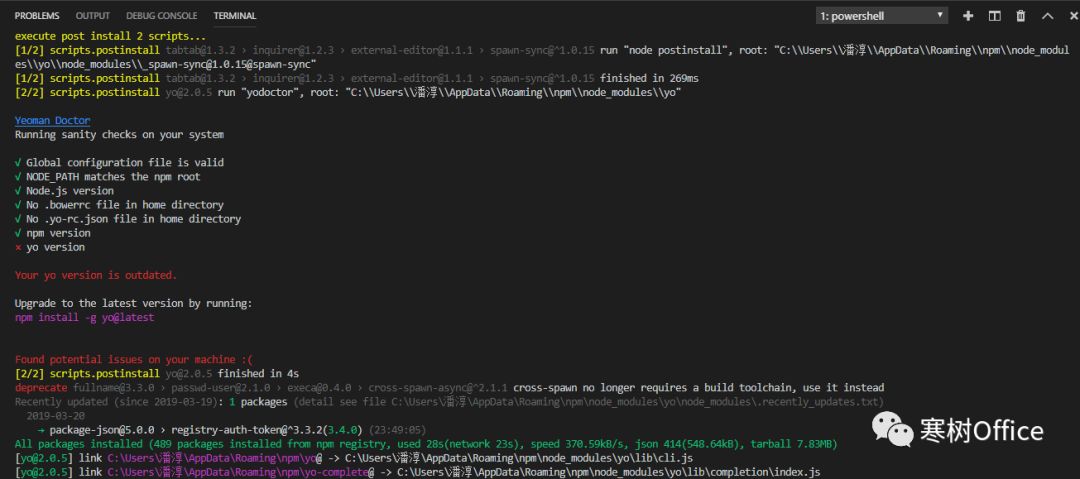
cnpm install -g yo

安装 yeoman，其中 install 是命令代表了安装，-g 是参数代表了全局，yo 是项目简称。安装过程竟然只需要半分就完成了：

【Office模板】

yoeman 其实是一个模板加载工具， 也叫生成器（generator），我们这里需在的是 Office 的模板，yoeman 还俱备查询功能，我们直接查询 Office 相关的模板。查到有两个跟Office相关的项目，我们得到了以下这条命令：

npm install -g generator-office

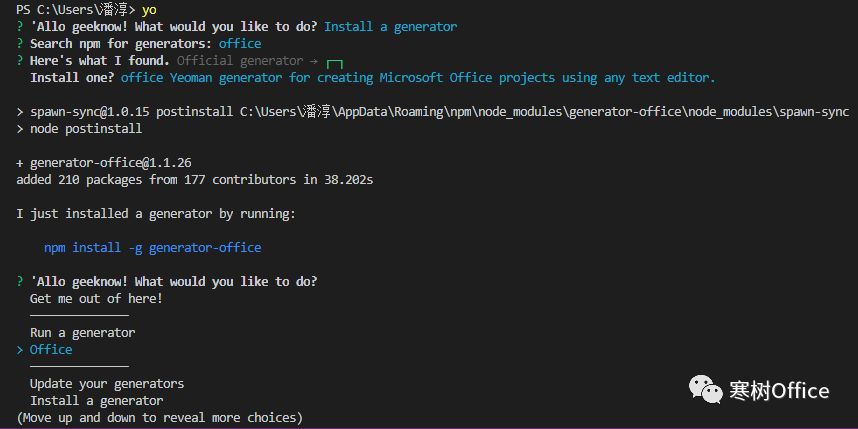
默认会安装最新的Office模板@1.1.26，但是我推荐使用@1.1.5版本，俱备可以选择不建目录，最后还会有一个设置导航。

npm install -g generator-office@1.1.5

在知道原理后，我这里再提供一个更简单的安装方法，这里两个可以一并安装了：

npm install -g yo generator-office@1.1.5

创建

【代码片段】

在 GitHubGist 上（https://gist.github.com/）组合搜索“yaml excel colorful”，其中 yaml 表示 Script Lab 代码片段，excel 表示这类插件，colorful 也可以替换所你感兴趣其它内容，以下为搜集结果：

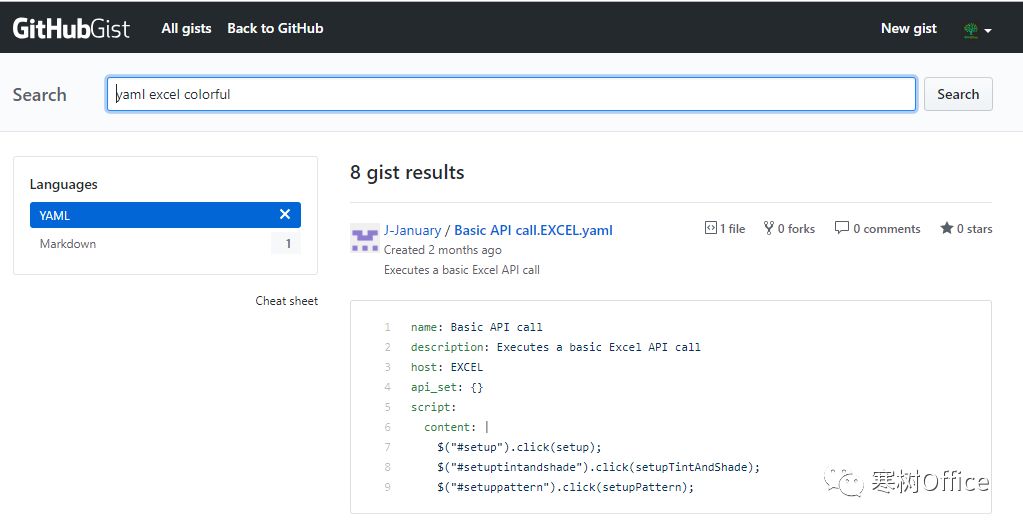
复制整个 yaml 格式的代码模板：

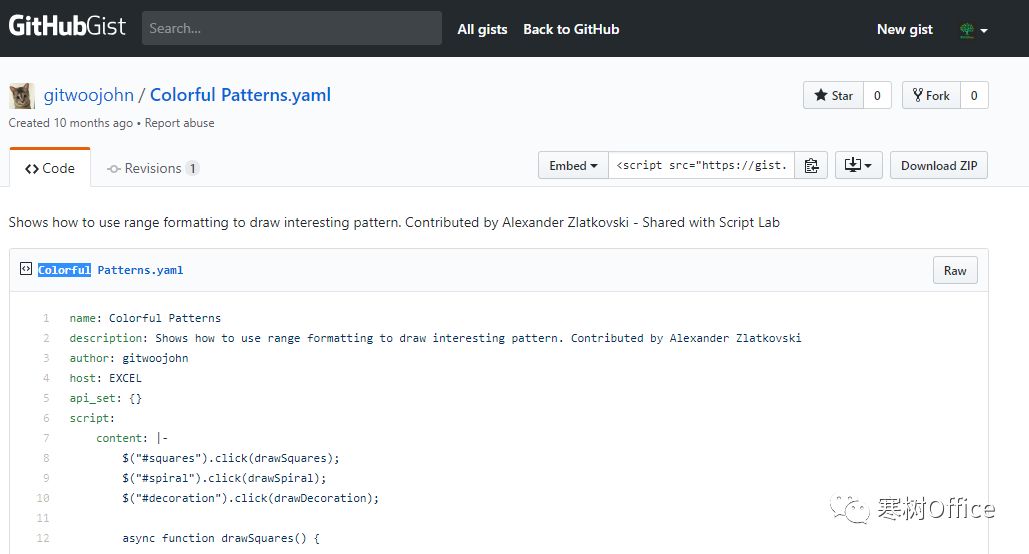
【导出清单代码】

将刚才复制的代码导入到 Script Lab 中，通过导入命令，贴入完整代码即可：

导出清单（manifest）和代码（html）

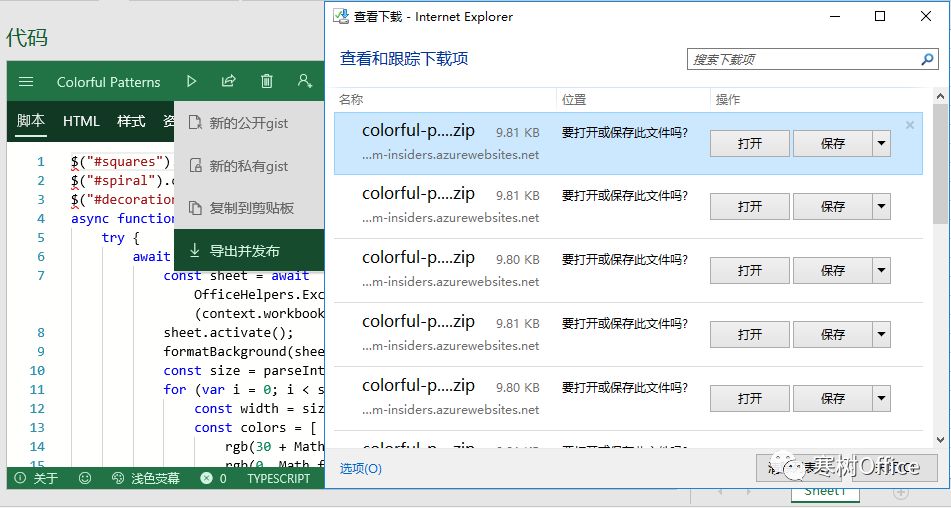
解压缩后得到，得到四个文件，新建一个目录，并将上面两个文件制复过去：

colorful-patterns.htmlcolorful-patterns--manifest.xmlcolorful-patterns--snippet-data.yamlREADME.md

【生成项目】

在 VSCODE 中，通过一句命令，来创建 Office Add-in 项目：

yo office

保留当前目录（Y），项目名称定一个（当前是：colorful-patterns），项目类型（Excel），创建项目代码，选择代码形式（TypeScript），项目生成后，选择项目引导（Y）。

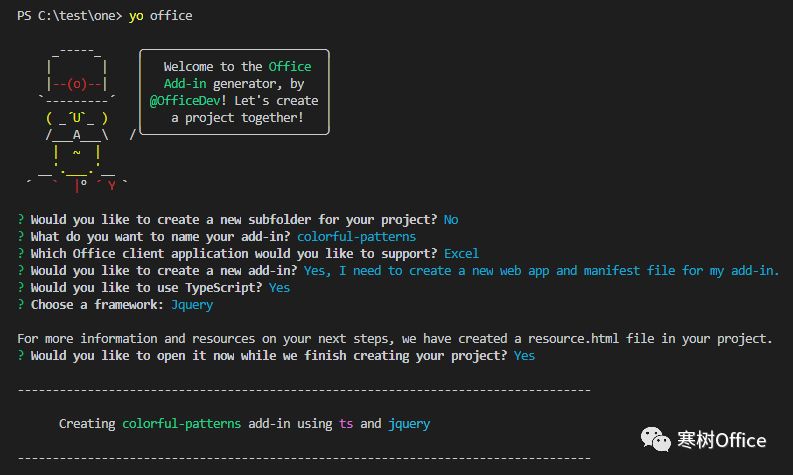
生成的文件目录结构如下：

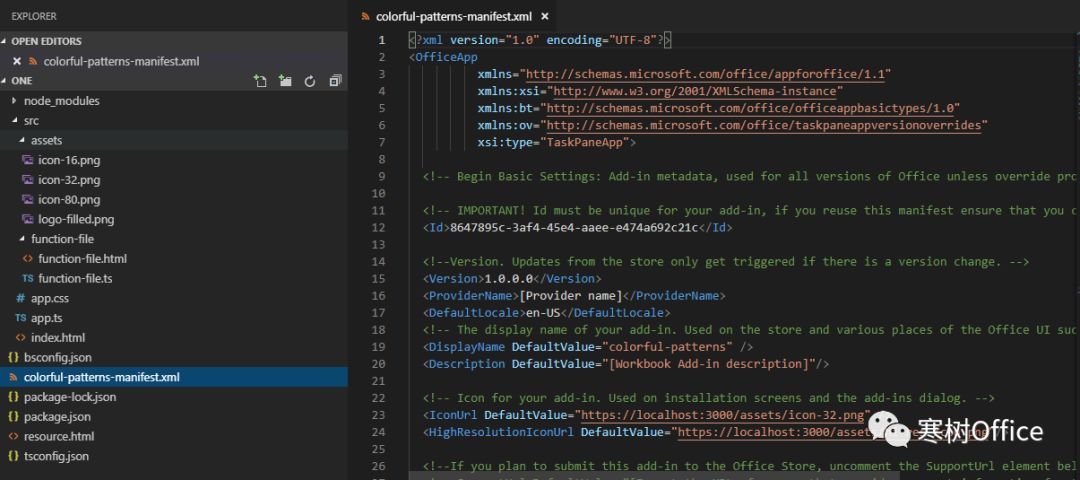
改造

【替换关键文件】

以下是教程的最关键点，你可以将之前导出的文件（manifest+html），将其复制并粘贴到现有项目中，就可以轻松将Script Lab 转转换功能完备的web add-ins 插件项目了。

colorful-patterns--manifest.xml 复制到根目录（对应 colorful-patterns-manifest.xml 可删）

colorful-patterns.html 复制到 Scr 目录下（对应 index.html，可删）

【修改清单文件】

修改清单文件：colorful-patterns--manifest.xml

清单文件后面的课程中将会专题介绍，这里只提一下几个关键的修改点，最重要的一点是替换启动页面，将默认的index.html改为Script Lab 生成的页面：

<bt:Url id="Contoso.Taskpane.Url" DefaultValue="https://localhost:3000/colorful-patterns.html" />

清单文件中所有文字的地方，进行汉化或修改：

<DisplayName DefaultValue="对照汉化！" /><Description DefaultValue="[对照汉化！]"/><bt:String id="Contoso.TaskpaneButton.Label" DefaultValue="对照汉化！" /><bt:String id="Contoso.Group1Label" DefaultValue="对照汉化！" /><bt:String id="Contoso.GetStarted.Title" DefaultValue="对照汉化！" /><bt:String id="Contoso.TaskpaneButton.Tooltip" DefaultValue="对照汉化！" /><bt:String id="Contoso.GetStarted.Description" DefaultValue="对照汉化！." />

【上传清单文件】

请按CTRL +`打开或返回集成终端。输入：

npm start

将在Chrome中打开您的项目。并可能会收到该站点不受信任的警告，单击“高级”并选择信任仍然/继续。或按照以下引导页进行认证主置，不在缀述：

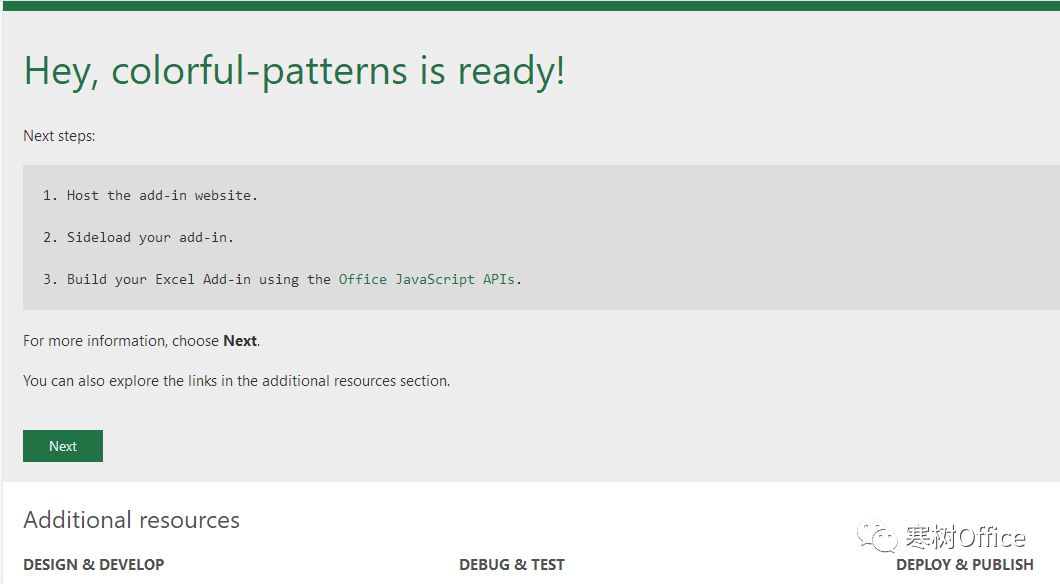
打开另一个选项卡，然后浏览到office365.com，登录帐户。在左上角的Office菜单上，单击Excel。在“插入”菜单上，单击“Office加载项”。在对话框的右上角，单击“上载我的加载项”。单击“浏览”，上传清单文件（colorful-patterns--manifest.xml）。的加载项现在将加载到“主页”选项卡上，切换到该选项卡，然后按“显示任务窗格”。

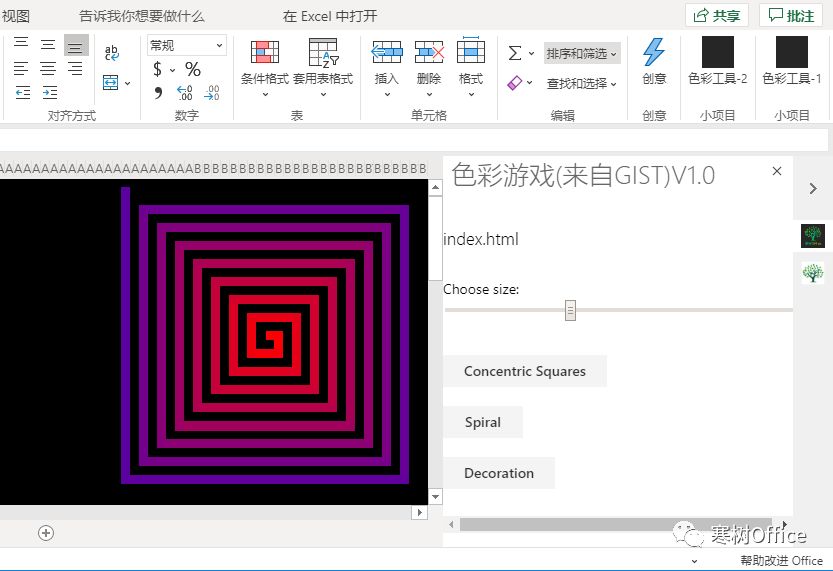
总结

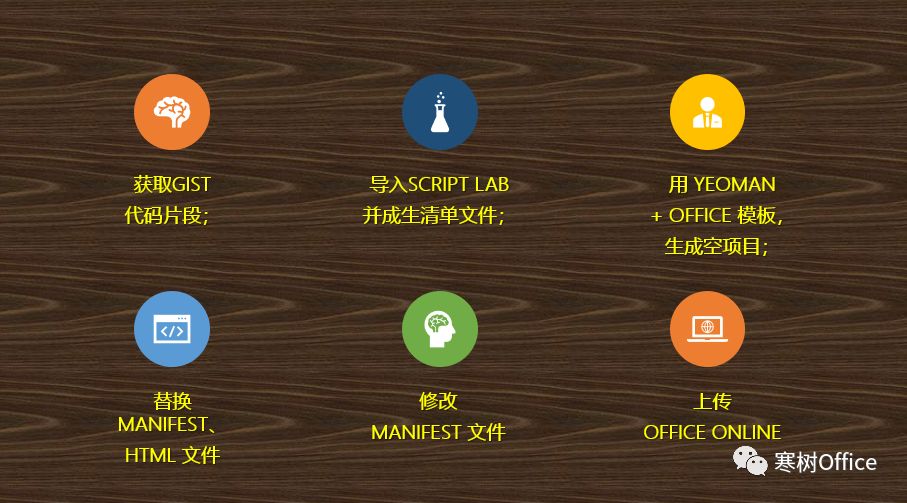
以上步骤将向你展示如何将 Script Lab 转为一个完整的 Web Add-ins 加载项目，Office Online中测试它。

1. 获取GIST代码片段；

2. 导入Script Lab 并成生清单文件；

3. 用 yeoman + Office 模板，生成空项目；

4. 替换 manifest、html 文件

5. 修改 manifest 文件

6. 上传 Office Online

 学习群

作者：寒树Office

介绍：Office 365 开发学习群（每日更新）

群号：976054900

 参加大会

欢迎您报名注册 Microsoft 365 DevDays (上海)，欢迎加群咨询。

日期：4月13日-14日，

地址：上海市，徐汇区，古美路1528号A7一楼漕河泾开发区会议中心，