autofixture简介

有了单元测试框架加上Moq(后面我们会用单独章节来介绍moq),可以说测试问题基上都能搞定了.然而有了AutoFixture对单元测试来说可以说是如虎添翼,AutoFixture并且它能与moq,rhinomock等框架结合,对单元测试带来的便捷性,可维护性和扩展性更是难以言表,只有用用了才知道.

说了这么多,还没有介绍AutoFixture是干什么的,其实AutoFixture就是一个假数据填充工具.

其实不论是Nunit还是Xunit都有数据填充功能,并且大部分时候都能满足需求.然而通过我们前面的介绍就会知道有以下问题:

• 不论是vlues注解还是TestCase注解都没有类型约束,这就可能会造成运行时错误.

• 基于注解的值都只能是Const值,如果需要复杂类型就需要定义一个类型做为Source为当前操作提供值.

• 与Nunit和Xunit生成的填充数据相比,Autofixture可以生成符合验证规则的数据(基于system.componentmodel.annotations名称空间下的注解约束),这在集成测试里帮助很大,对于有着非常复杂模型验证的接口来说,手工制造出符合模型验证规则的数据往往是非常痛苦的.

• Autofixture可以生成一组符合验证规则的数据,这样在测试的时候增加了样本数据的随机性,大大提升了测试的覆盖面.

Moq测试虽然极大方便了测试,但是也会有一些问题:

• 对于比较复杂的web项目,往往一个业务逻辑可能要消费十个几个甚至几十个数据接口,如果业务不是很成熟可能需要不断的来调整这些接口,这里的修改同时单元测试方法也需要修改(因为这些接口多数时候是通过构造函数注入的,构造函数参数数量的变动会导致调用者也需要做相应调整)

• 虽然Moq也能够模拟类对象,但是限制非常多,我们不可能为了测试把所有的方法和属性都加上abstract或者virtual.

而autofixture则可以很好的解决这些问题.这样极大增加代码的可维护性和扩展性.

AutoFixture并不是对moq的替代,它只能填充对象,而不能模拟对象,但是它可以与moq框架结合实现更强大的功能.

autofixture安装

autofixture安装非常简单,我们在Nuget里搜索autofixture,第一个就是它点击安装即可.

关于autofixture与moq结合需要的包在后面讲到的时候再安装,这里先略过.

要使AutoFixture与Nunit结合,首先我们需要安装特定的包.

在Nuget里输入AutoFixture.Nunit3,会出现以下选项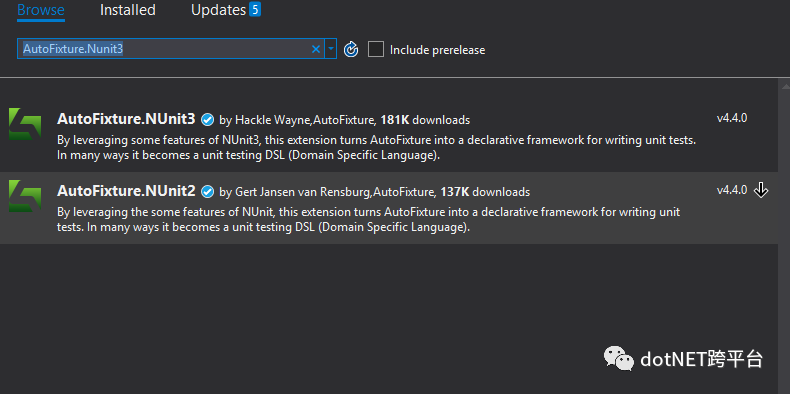

AutoFixture还可以与Xunit结合.在Nuget里搜索AutoFixture.xunit2便可以搜索到AutoFixture与Xunit结合的框架.与Xunit结果的用法与Nunit差不多,只是需要注意Xunit数据测试方法需要Theory注解.

我们新建一个名为FixtureTest并引入AutoFixture.NUnit3;名称空间

代码如下

 [TestFixture]public class FixtureTest{[Test][AutoData]public void FixValueTest(int a, int b){var result = Add(a , b);Assert.AreEqual(a + b, result);}int Add(int x, int y){return x + y;}}

这里与平时的单元测试相比,多了一个AutoData注解,有了AutoData注解,AutoFixture便可以给当前测试提供值了.

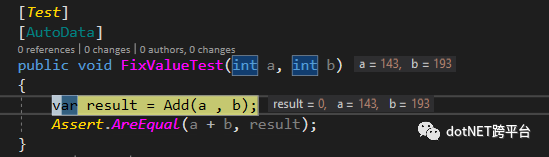
我们可以看到a和b都被赋予了随机的值.

我们把测试代码改为如下

        [Test][AutoData]public void FixValueTest(Person p1, Person p2){var result = Add(p1.Age , p2.Age);Assert.AreEqual(p1.Age + p2.Age, result);}

我们再断点调试一下看看是否有值

复杂对象它也能填充!这样就免去了为了使用复杂对象需要额外写很多source繁琐.

我们把代码改成如下

我们看看此时会有什么结果

通过监视容器可以看到,AutoFixture生成了一个包含三个元素的对象.

这简直是太方便了,autofixture自动填充值不但减少了运行时可能的类型错误,还有极大的扩展性,如果我们在测试方法上添加其它参数,它仍然能够自动填充.而使用Nunit自身带的TestCase如果参数减少,里面指定的值也要减少,否则会抛出运行时异常.

通过以上我们可以看到,AutoFixture可以生成各种类型的对象,它可以创建集合对象对我们测试来说尤其有用,免去了手动创建的麻烦.但是我们同时也看到,基于注解的方法生成集合时只生成了三个,实际上要模拟数据库是的数据测试一些行为我们可能需要更多的元素.这里就需要对AutoFixture本身进行配置.这是基于注解的方法无法完成的.