常见算法（JavaScript版）

持续更新中…

排序

假设以下所有排序都是升序

快速排序在大部分情况下是效率最高的，所以笔试的时候要求写排序算法，能写快速排序就尽量写快速排序。

为后续讲解做铺垫，先封装ArrayList类如下。待排序的数组array是这个类的属性，里面存储了列表排序的方法（升序）、插入数组元素及打印数组的方法。

function ArrayList(){this.array=[]// 向数组插入元素ArrayList.prototype.insert=function(item){this.array.push(item)}// 打印数组元素ArrayList.prototype.toString=function(){return this.array.join()}// 因为该ArrayList类会多次使用交换的操作，故此处封装次操作ArrayList.prototype.swap=function(m,n){let temp=this.array[m]this.array[m]=this.array[n]this.array[n]=temp}
}

测试代码

let arr= new ArrayList()
arr.insert(11)
arr.insert(90)
arr.insert(0)
arr.insert(9)
arr.insert(19)
// alert默认会调用参数的toString方法
alert(arr)

在这里插入图片描述

冒泡排序

原理详见https://www.bilibili.com/video/BV1x7411L7Q7

// 冒泡排序
ArrayList.prototype.bubbleSort=function(){let length=this.array.length// 外层循环j变量控制每轮比较的终止位置for(let j=length-1;j>=1;j--){// 内层循环i表示当前正在比较的位置for(i=0;i<j;i++){if(this.array[i]>this.array[i+1]){this.swap(i,i+1)}}}
}

测试代码

let arr= new ArrayList()
arr.insert(11)
arr.insert(90)
arr.insert(0)
arr.insert(9)
arr.insert(19)
// alert默认会调用参数的toString方法
alert(arr)
arr.bubbleSort()
alert(arr)

在这里插入图片描述

冒泡排序的效率：
对于测试代码中的5个数组元素，比较次数为：4 + 3 + 2 + 1;
对于N个数据项，比较次数为：(N - 1) + (N - 2) + (N - 3) + … + 1 = N * (N - 1) / 2；
所以时间复杂度： $O(n^2)$
交换次数：每次比较有交换和不交换的情况，取平均，那交换次数就是比较次数的一半，所以交换次数= $1/2 * n (n - 1) /2 = 1/4 * n (n - 1)$ ，也是 $O(n^2)$ 的复杂度

选择排序

// 选择排序
// 每轮查找最小的元素放到前面
ArrayList.prototype.selectSort=function(){let length=this.array.length// 外层循环j变量控制每轮查找的起始位置for(let j=0;j<length-1;j++){// 先假定起始位置的元素是本轮最小的值，min存储每轮最小元素的下标let min=j// 内层循环i表示当前正在比较的位置for(i=j;i<length;i++){if(this.array[i]<this.array[min]){min=i}}this.swap(j,min)}
}

测试代码

let arr= new ArrayList()
arr.insert(11)
arr.insert(90)
arr.insert(0)
arr.insert(9)
arr.insert(19)
// alert默认会调用参数的toString方法
alert(arr)
arr.selectSort()
alert(arr)

在这里插入图片描述
选择排序的效率：
选择排序的比较次数与冒泡排序一样，为：N * (N - 1) / 2，用大O表示法表示为： $O（N^2）$ ;
选择排序的交换次数最多为(N-1)次，平均为：(N - 1) / 2，用大O表示法表示为：O（N）;
选择排序平均交换次数少于冒泡排序，所以效率高于冒泡排序；

插入排序

插入排序的思路：
插入排序思想的核心是局部有序。如图所示，X左边的人称为局部有序；
首先指定一数据X（从第一个数据开始），并将数据X的左边变成局部有序状态；
随后将X右移一位，再次达到局部有序之后，继续右移一位，重复前面的操作直至X移至最后一个元素。
插入排序的详细过程：
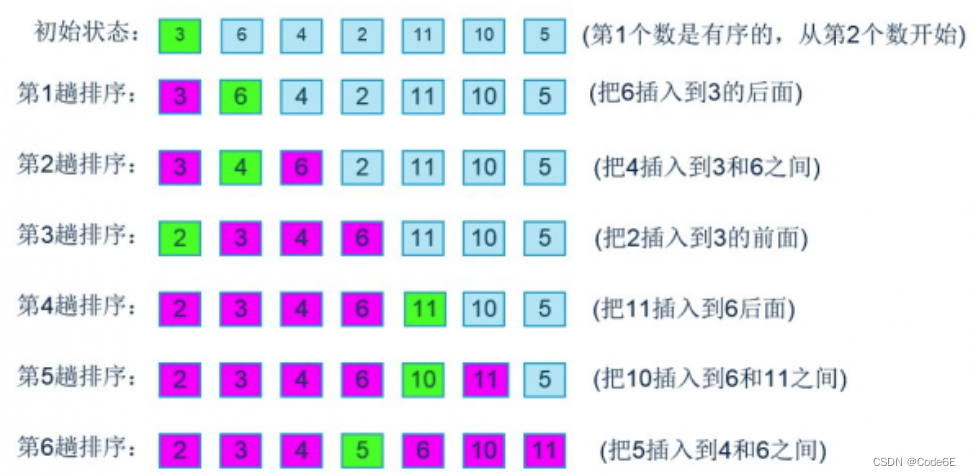
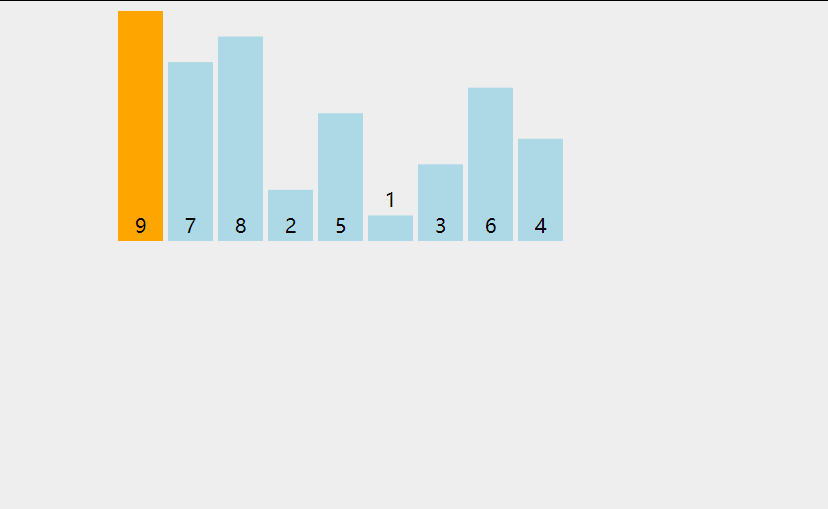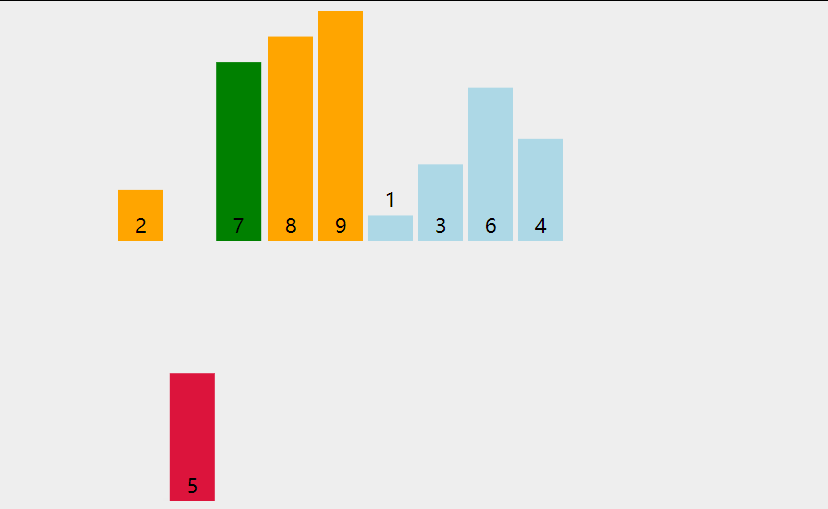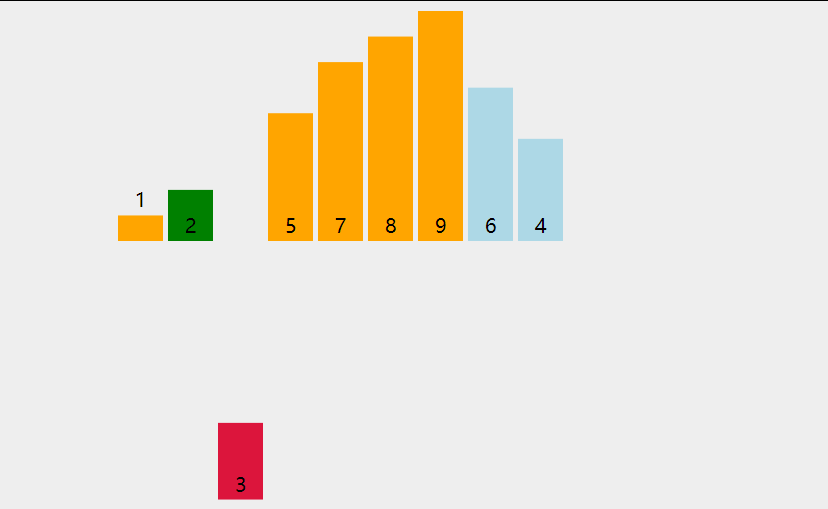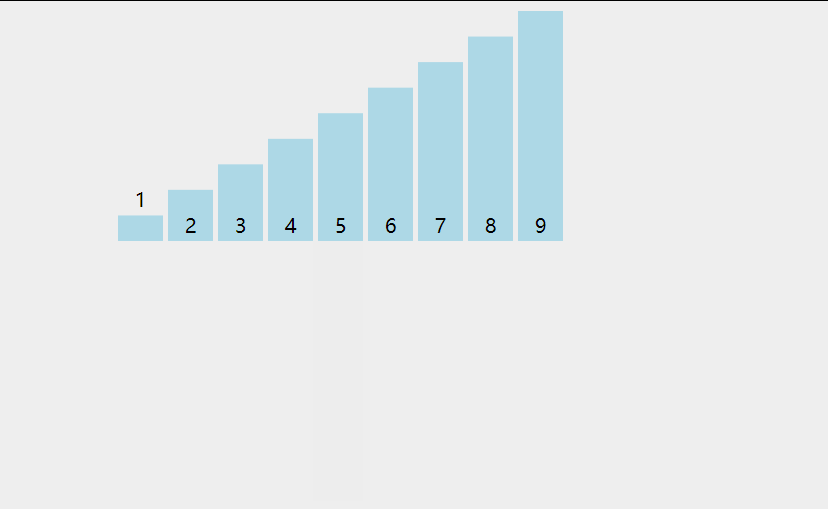
在这里插入图片描述

在这里插入图片描述

代码实现

// 插入排序
ArrayList.prototype.insertSort=function(){let length=this.array.length// 外层循环j变量表示当前要插入元素所处的位置for(let j=1;j<length;j++){// 因为this.array[j]待会可能被覆盖，所以要用变量暂存下let temp=this.array[j]// 从j开始往左比较let i=j// 要插入的元素与左边的元素比较大小，寻找最终要插入的位置while(temp<this.array[i-1] && i>=1){// 在找到最终要插入的位置前，左边原有的元素右移一位this.array[i]=this.array[i-1]i--}// 找到最终要插入的位置后，将该元素值放入该位置this.array[i]=temp}
}

插入排序的效率：

比较次数：第一趟时，需要的最大次数为1；第二次最大为2；以此类推，最后一趟最大为N-1；所以，插入排序的总比较次数最多为N * (N - 1) / 2；平均比较次数大概为：N * (N - 1) / 4；
赋值次数：指定第一个数据为X时赋值0次，指定第二个数据为X最多需要赋值1次，以此类推，指定第N个数据为X时最多需要赋值N - 1次，总赋值次数最多为N * (N - 1) / 2次，平均赋值次数大概为：N * (N - 1) / 4；
虽然插入排序的效率也是 $O（N^2）$ ，但插入排序没有交换的操作，赋值消耗的性能比交换操作小，插入排序比较和赋值的次数总共才为N(N-1)/2，相当于冒泡排序和选择排序比较的次数，所以是简单排序中效率最高的算法

以上都是简单排序（冒泡，选择，插入），时间复杂度都是 $O（N^2）$ 。下面的高级排序时间复杂度能低于 $O（N^2）$

希尔排序

详见

某位网友的博客（本文没有对希尔排序做详细的说明，详见这篇博客）
codewhy视频

插入排序的问题：

如果一个很小的数据项在很靠近右端的位置上（这里本应该是较大的数据项的位置），将这个小数据项移动到正确的位置，需要其左侧很多元素右移一位，这样效率非常低；
如果通过某种方式，先让较小的元素整体靠近左侧，较大的元素整体靠近右侧，数组处于基本有序的状态，则元素做插入排序的时候就不会一个个移动其左侧的大量元素，那么算法的效率将有很大的提升。

希尔排序的思想：按照增量将排列分组，每一组用插入排序排好序，再逐渐减小增量，再排序，直至增量为1，这时整个排列较小的数基本靠左，较大的数基本靠右，这时再用插入排序，移位的次数会少很多，所以效率优于插入排序，是插入排序的改进版。

希尔排序的历史背景：

希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布；
希尔算法首次突破了计算机界一直认为的算法的时间复杂度都是O（N^2）的大关，为了纪念该算法里程碑式的意义，用Shell来命名该算法

排序过程：
假设要排序数组[81, 94,11, 96,12,35, 17, 95, 28, 58, 41, 75, 15]
设初始增量为5，分组如下，共分成了5组（一般增量是几就分成了几组）
在这里插入图片描述
将每组排好序（一般用插入排序排好序），再按增量3分组，如下

3间隔排好序如下

最后1间隔排好序如下

增量选择：
在这里插入图片描述

复杂度：希尔排序的效率和增量的选择关系比较大，但复杂度都小于 $O（N^2）$

代码：

            // 希尔排序ArrayList.prototype.shellSort = function () {let length = this.array.length// 这里增量采取的是希尔原稿中建议的，就是不断折半gap=Math.floor(gap/2)，直至最后gap=1let gap = Math.floor(length / 2)//gap初始值是数组长度一半的整数while (gap >= 1) {/* 这一部分的for循环和插入排序差不多，就是步进值由1变成了gap。---start--- */// 由增量分组做插入排序，以使数组达到基本有序的状态（比如对于升序排列，较小的值基本靠左，较大的值基本靠右）// 外层循环j变量表示当前要插入元素所处的位置for (let j = gap; j < length; j++) {// 因为this.array[j]待会可能被覆盖，所以要用变量暂存下let temp = this.array[j]// 从j开始往左比较let i = j// 要插入的元素与左边同组的元素比较大小，寻找最终要插入的位置// i >= gap确保下标不为负数while (temp < this.array[i - gap] && i >= gap) {// 在找到最终要插入的位置前，左边原有的元素右移一位this.array[i] = this.array[i - gap] i -= gap}// 找到最终要插入的位置后，将该元素值放入该位置this.array[i] = temp}/* 这一部分的for循环和插入排序差不多，就是步进值由1变成了gap。---end--- */gap=Math.floor(gap/2)}}

测试代码

let arr = new ArrayList()
arr.insert(8)
arr.insert(9)
arr.insert(1)
arr.insert(7)
arr.insert(2)
arr.insert(3)
arr.insert(5)
arr.insert(4)
arr.insert(6)
arr.insert(0)
// alert默认会调用参数的toString方法
alert(arr)
arr.insertSort()
alert(arr)

在这里插入图片描述

快速排序（必须掌握）

参见书籍《大话数据结构》
思想：从排列中选取一个数作为枢纽，使得该排列所有小于枢纽的数都在枢纽的一边，所有大于枢纽的数都在枢纽的另一边。然后对子排列递归地这样操作，直到整个排列达到有序状态。
快速排序用了分治算法的思想，就是将一个大问题分成许多相同的小问题（解决思路一样，只是问题规模可能不一样），递归地去解决这些问题

代码（这是未优化的情况，即默认排列第一个数为枢纽）

// 测试数据
let arr=[5,1,9,3,7,4,8,6,2];// 交换操作
function swap(arr,m, n) {let temp = arr[m]arr[m] = arr[n]arr[n] = temp
}// 找到枢纽下标值（快速排序核心代码）
function partition(L, left, right) {// 假设排列第一个数为枢纽，该枢纽会随着之后的交换逐渐移动到排列的合适位置let pivotValue=L[left]// 跳出该循环时，left==right，这时swap(L,left,right)不会影响已经排好的数列while (left < right) {while (left < right && L[right] >=pivotValue) right--; // 从右侧下标递减，直到找到比枢纽小的数swap(L,left,right); // 交换下标为left和right的值while (left < right && L[left] <=pivotValue) left++; // 从左侧下标递增，直到找到比枢纽大的数swap(L,left,right); // 交换下标为left和right的值}return left // 最终left==right，所以return right也行
}function quickSort(L, left, right) {if (left < right) {let pivot = partition(L, left, right) // 获取枢纽下标quickSort(L, left, pivot - 1)quickSort(L, pivot + 1, right)return L}
}console.log( quickSort(arr, 0, arr.length - 1));