利用树的先序和后序遍历打印os中的目录树

【0】README
0.1）本代码均为原创，旨在将树的遍历应用一下下以加深印象而已；（回答了学习树的遍历到底有什么用的问题？）你对比下linux 中的文件树 和我的打印结果就明理了；

0.2）我们采用的是 儿子兄弟表示法 来 表示树的整体节点构造；
0.3）儿子兄弟表示法介绍
0.3.1）如下图所示： 向下的箭头（左指针）指向第一个儿子节点， 从左到右的箭头（右指针）指向下一个兄弟节点；（间接说明了树的节点有两个指针）
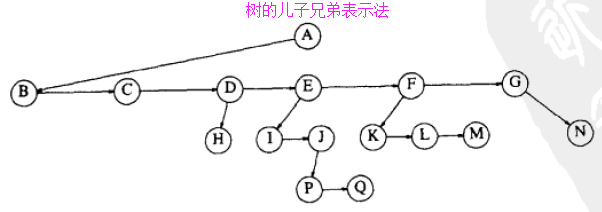
0.3.2）树节点定义代码如下：
struct Tree;
typedef struct Tree *Tree;// we adopt child-sibling notation
struct Tree
{ElementType value;Tree firstChild;Tree nextSibling;
};
0.4）哥子第一次 使用着 丑到逼爆 的 编辑器，也是醉了，主要是markdown 对于源代码文件显示不够清晰， oh m g；

【1】任务来了
我们想要列出目录中所有文件的名字， 我们的输出格式将是：深度为 depth 的文件的名字将被 depth 次跳格缩进后打印出来；
【2】给出先序遍历+后序遍历目录树的实现代码
2.1）先序遍历步骤：
step1）访问根节点；
step2）先序遍历以儿子为根的子树；
step3）先序遍历以兄弟为根的子树；
download source code：https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter4/p68_preorder_common_tree.c

source code at a glance： 
#include <stdio.h>
#include <malloc.h>#define ElementType char
#define Error(str) printf("\n error: %s \n",str)   struct Tree;
typedef struct Tree *Tree;Tree createTree();
Tree makeEmpty(Tree t);
Tree insert(ElementType e, Tree t);// we adopt child-sibling notation
struct Tree
{ElementType value;Tree firstChild;Tree nextSibling;
};// create a tree with root node
Tree createTree()
{	Tree t;t = (Tree)malloc(sizeof(struct Tree));if(!t) {Error("out of space, from func createTree");        return NULL;}    t->firstChild = NULL;t->nextSibling = NULL;	t->value = '/';return t;
}// make the tree empty 
Tree makeEmpty(Tree t)
{if(t){makeEmpty(t->firstChild);makeEmpty(t->nextSibling);		free(t);}			return NULL;
}//
Tree insert(ElementType e, Tree parent)
{Tree child;Tree newSibling;if(!parent){Error("for parent tree node is empty , you cannot insert one into the parent node, from func insert");        return NULL;}newSibling = (Tree)malloc(sizeof(struct Tree));if(!newSibling) {Error("out of space, from func insert");        return NULL;}newSibling->value = e;newSibling->nextSibling = NULL;newSibling->firstChild = NULL;// building the node with value e overchild = parent->firstChild;	if(!child) {parent->firstChild = newSibling;return parent;}while(child->nextSibling)child = child->nextSibling; // find the last child of parent nodechild->nextSibling = newSibling;return parent;
}// find the tree root node with value equaling to e
Tree find(ElementType e, Tree root)
{Tree temp;if(root == NULL)return NULL;if(root->value == e)return root;temp = find(e, root->firstChild);	if(temp) return temp;elsereturn 	find(e, root->nextSibling);				
}// analog print directories and files name in the tree, which involves preorder traversal.
void printPreorder(int depth, Tree root)
{			int i;if(root) {		for(i = 0; i < depth; i++)printf("    ");printf("%c\n", root->value);			printPreorder(depth + 1, root->firstChild);									printPreorder(depth, root->nextSibling);} 
}int main()
{Tree tree;tree = createTree();printf("\n test for insert 'A' 'B' into the parent '/' and 'C' 'D' into the parent 'A' \n");	insert('A', tree);	insert('B', find('/', tree));	insert('C', find('A', tree));insert('D', find('A', tree));printPreorder(1, tree);printf("\n test for insert 'E' 'F' into the parent '/'  \n");	insert('E', find('/', tree));insert('F', find('/', tree));printPreorder(1, tree);printf("\n test for insert 'G' 'H' into the parent 'E' and 'I' into the parent 'H' and even 'J' 'K' into the parent 'I' \n");	insert('G', find('E', tree));insert('H', find('E', tree));insert('I', find('H', tree));insert('J', find('I', tree));insert('K', find('I', tree));printPreorder(1, tree);return 0;
}

打印结果如下：


2.2）后序遍历步骤：（不同于二叉树的后序）
step1）后序遍历以儿子为根的子树；
step2）访问根节点；
step3）后序遍历以兄弟为根的子树；
download source code：https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter4/p69_postorder_commone_tree.c

source code at a glance:
#include <stdio.h>
#include <malloc.h>#define ElementType char
#define Error(str) printf("\n error: %s \n",str)   struct Tree;
typedef struct Tree *Tree;Tree createTree();
Tree makeEmpty(Tree t);
Tree insert(ElementType e, Tree t);// we adopt child-sibling notation
struct Tree
{ElementType value;Tree firstChild;Tree nextSibling;
};// create a tree with root node
Tree createTree()
{	Tree t;t = (Tree)malloc(sizeof(struct Tree));if(!t) {Error("out of space, from func createTree");        return NULL;}    t->firstChild = NULL;t->nextSibling = NULL;	t->value = '/';return t;
}// make the tree empty 
Tree makeEmpty(Tree t)
{if(t){makeEmpty(t->firstChild);makeEmpty(t->nextSibling);		free(t);}			return NULL;
}//
Tree insert(ElementType e, Tree parent)
{Tree child;Tree newSibling;if(!parent){Error("for parent tree node is empty , you cannot insert one into the parent node, from func insert");        return NULL;}newSibling = (Tree)malloc(sizeof(struct Tree));if(!newSibling) {Error("out of space, from func insert");        return NULL;}newSibling->value = e;newSibling->nextSibling = NULL;newSibling->firstChild = NULL;// building the node with value e overchild = parent->firstChild;	if(!child) {parent->firstChild = newSibling;return parent;}while(child->nextSibling)child = child->nextSibling; // find the last child of parent nodechild->nextSibling = newSibling;return parent;
}// find the tree root node with value equaling to e
Tree find(ElementType e, Tree root)
{Tree temp;if(root == NULL)return NULL;if(root->value == e)return root;temp = find(e, root->firstChild);	if(temp) return temp;elsereturn 	find(e, root->nextSibling);				
}// analog print directories and files name in the tree, which involves postorder traversal. 
void printPostorder(int depth, Tree root)
{			int i;if(root) {						printPostorder(depth + 1, root->firstChild);											for(i = 0; i < depth; i++)printf("    ");		printf("%c\n", root->value);			printPostorder(depth, root->nextSibling);} 
}int main()
{Tree tree;tree = createTree();printf("\n ====== test for postordering the common tree presented by child_sibling structure  ====== \n");	printf("\n test for insert 'A' 'B' into the parent '/' and 'C' 'D' into the parent 'A' \n");	insert('A', tree);	insert('B', find('/', tree));	insert('C', find('A', tree));insert('D', find('A', tree));printPostorder(1, tree);printf("\n test for insert 'E' 'F' into the parent '/'  \n");	insert('E', find('/', tree));insert('F', find('/', tree));printPostorder(1, tree);printf("\n test for insert 'G' 'H' into the parent 'E' and 'I' into the parent 'H' and even 'J' 'K' into the parent 'I' \n");	insert('G', find('E', tree));insert('H', find('E', tree));insert('I', find('H', tree));insert('J', find('I', tree));insert('K', find('I', tree));printPostorder(1, tree);return 0;
}

打印结果如下：


本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/332029.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Hibernate常用API

Hibernate常用API

文章目录删除指定的记录新增记录更新记录清空缓存将实体对象从缓存中清除将缓存中更新的数据同步到数据库把数据库中的数据刷到缓存中查询多个对象&#xff08;也就是查询多条记录&#xff09;查询指定ID的对象&#xff08;查询指定ID值的记录&#xff09;参考删除指定的记录 U…
阅读更多...
solid设计原则_SOLID设计原则

solid设计原则_SOLID设计原则

solid设计原则介绍&#xff1a; Robert C. Martin定义了五项面向对象的设计原则&#xff1a; 小号英格尔-责任原则 笔封闭原则 大号 iskov的替换原则 我覆盖整个院落分离原则&#xff0c;并 d ependency倒置原则 这些一起被普遍称为SOLID原则。 在设计面向对象的系统时&a…
阅读更多...
nosql简答什么是最终一致性_NoSql的三大基石：CAP理论BASE最终一致性

nosql简答什么是最终一致性_NoSql的三大基石：CAP理论BASE最终一致性

关系型数据库的局限NoSql出现在关系型数据库之后&#xff0c;主要是为了解决关系型数据库的短板&#xff0c;我们先来看看随着软件行业的发展&#xff0c;关系型数据库面临了哪些挑战&#xff1a;1、高并发一个最典型的就是电商网站&#xff0c;例如双11&#xff0c;几亿大军的…
阅读更多...
二叉树的先中后序遍历

二叉树的先中后序遍历

【0】README 0.1&#xff09;本文旨在理清二叉树的先中后序遍历&#xff0c; 以及如何建立二叉树等相关内容&#xff1b; 0.2&#xff09;本文涉及代码均为原创&#xff1b; 0.3&#xff09;本文中遍历后的打印结果&#xff0c;朋友您可以直接写出二叉树的节点构造出来&…
阅读更多...
表达式树

表达式树

【0】README 0.1&#xff09;本文旨在总结出表达式树的构建步骤&#xff0c; 其中还涉及到中缀转后缀表达式&#xff0c;以及如何计算 表达式树中的值&#xff1b; 0.2&#xff09;本文源代码均为原创&#xff1b; 0.3&#xff09; 其实&#xff0c; 实现一个简单的计算器&a…
阅读更多...
Date/Timestamp/String/LocalDate/LocalDateTime

Date/Timestamp/String/LocalDate/LocalDateTime

文章目录String 转成 DateDate 转成 StringString 转成 Timestamp获取系统当前的毫秒数获取系统当前的日期时间毫秒数转成 Timestamp毫秒数转成 DateTimestamp 转成 StringDate 转成 TimestampTimestamp 转成 Datejava.util.Date 转成 java.sql.Date将带T的日期时间转成正常的日…
阅读更多...
python可以用来写什么工具_python写工具

python可以用来写什么工具_python写工具

谷歌开源 Python Fire&#xff1a;可自动生成命令行接口今天我们很高兴地宣布 Python Fire 开源。Python Fire 可从任何 Python 代码生成命令行接口(command line interfaces (CLIs))&#xff0c;简单地调用任意 Python 程序中的 Fire 函数以将那个程序自动地转化为 CLI。该库可…
阅读更多...
java原始类型和引用类型_Java中的8种原始类型

java原始类型和引用类型_Java中的8种原始类型

java原始类型和引用类型几年前&#xff0c;当我开始编辑Java Basics系列时&#xff0c;我认为将一些非常详细的信息拉到自己的帖子中是很有意义的。 这样&#xff0c;初学者的内容就更容易消化了。 首先&#xff0c;我将介绍有关Java的8种原始类型的所有信息。 Java基本类型 正…
阅读更多...
androidtabhost缓存_FragmentTabHost布局的使用及优化方式

androidtabhost缓存_FragmentTabHost布局的使用及优化方式

欢迎Follow我的GitHub, 关注我的简书. 其余参考Android目录.TabHostAndroidFragmentTabHost作为Android4.0版本的控件, 已经被项目广泛使用, 5.0版本又推出TabLayoutViewPager显示多页. 我来讲解如何使用FragmentTabHost.本文源码的GitHub下载地址主要包括:(1) 自定义Tab的图片…
阅读更多...
二叉查找树

二叉查找树

【0】README 0.1&#xff09;本文的重点在于介绍 二叉查找树的概念&#xff0c;以及写出 二叉查找树的操作例程的源代码&#xff0c; 其中当属delete 操作的源代码最不容易实现&#xff1b; 0.2&#xff09;本文源代码均为原创&#xff0c; 当然 代码中的idea 是借鉴人家的&a…
阅读更多...
常用的命名规范/命名规则

常用的命名规范/命名规则

文章目录骆驼式命名法&#xff08;CamelCase&#xff09;帕斯卡命名法&#xff08;PascalCase&#xff09;串式命名法&#xff08;KebabCase&#xff09;下划线命名法&#xff08;UnderScoreCase&#xff09;骆驼式命名法&#xff08;CamelCase&#xff09; 也叫小驼峰式命名法…
阅读更多...
spring order_Spring @Order批注

spring order_Spring @Order批注

spring order介绍&#xff1a; Spring Order注释是在Spring 2.0中首次引入的。 然后&#xff0c;它仅用于定义AspectJ建议中的顺序。 在Spring 4.0的后面&#xff0c;对该注释的实现进行了进一步改进。 从那时起&#xff0c;它还支持对Java数组或List之类的集合中的Spring组件或…
阅读更多...
AVL树

AVL树

【0】README 0.1&#xff09;本文给出了平衡二叉树&#xff08;AVL树&#xff09;的插入例程涉及到的单旋转双旋转的概念&#xff0c;并给出了代码实现&#xff1b; 0.2&#xff09;本文源代码均为原创&#xff0c; 当然相关idea 还是借鉴人家的&#xff1b;&#xff08;真心…
阅读更多...
spring 注释_Spring@懒惰注释

spring 注释_Spring@懒惰注释

spring 注释介绍&#xff1a; 默认情况下&#xff0c; Spring框架在应用程序启动时加载并热切初始化所有bean。 在我们的应用程序中&#xff0c;我们可能有一些非常消耗资源的bean。 我们宁愿根据需要加载此类bean。 我们可以使用Spring Lazy批注实现此目的 。 在本教程中&…
阅读更多...
管理系统的账户设计（涉及注册/登录逻辑）

管理系统的账户设计（涉及注册/登录逻辑）

文章目录方案一方案二方案三方案一 类似华为云IAM&#xff08;Identity and Access Management 身份和访问管理&#xff09;用户&#xff0c;阿里云的 RAM&#xff08;Resource Access Management 资源访问管理&#xff09;用户 机构有独立的账户&#xff08;主账户&#xff…
阅读更多...
opencv生成日志_OpenCV-Utils学习日志：VideoCapture使用样例

opencv生成日志_OpenCV-Utils学习日志：VideoCapture使用样例

1.VideoCapture可以打开多种来源的数据流&#xff0c;但常见的是相机、视频及图像序列三类数据流&#xff1a;(1)打开相机数据流&#xff0c;需要指定相机在主机上的设备编号&#xff0c;若主机上只有一个相机则编号通常是0。(2)打开视频数据流&#xff0c;需要指定视频的完整路…
阅读更多...
jdbc查询序列_JDBC –模拟序列

jdbc查询序列_JDBC –模拟序列

jdbc查询序列也许我们每个人在程序员的生活中至少遇到过一次这个问题- 如何模拟数据库序列&#xff1f; 在下面&#xff0c;您可能会发现我对该问题解决方案的各种了解。 假设我们有一个接口定义了所需的API&#xff0c;用于返回整数序列&#xff1a; public interface Sequen…
阅读更多...
利用 GregorianCalendar 制作当前月的月历

利用 GregorianCalendar 制作当前月的月历

【0】README 0.1&#xff09;本文文字总结于 core java volume 1 &#xff0c; 源代码均为原创&#xff1b; 0.2&#xff09;本文旨在熟悉 GregorianCalendar 日历类&#xff0c;每一天就是一个GregorianCalendar 日历类&#xff0c;一天有很多的日历属性&#xff0c;觉得用它…
阅读更多...
pyecharts怎么绘制散点图_PyeCharts绘制各种图形

pyecharts怎么绘制散点图_PyeCharts绘制各种图形

简介PyeCharts 是一个用于生成 Echarts 图表的类库&#xff0c;用其生成的图可视化效果非常棒&#xff0c;而且使用起来非常简单。下面是一些常用图的pyecharts实现方法柱状图bar pye.Bar("柱状图")#新建柱状图bar.add("服装", #图例名称["衬衫"…
阅读更多...
junit junit_穿越JUnit流

junit junit_穿越JUnit流

junit junit关于JUnit 5迁移的好处之一是&#xff0c;您可以在老式模式下运行JUnit 4测试&#xff0c;并且所有内容仍然兼容。 不利的一面是&#xff0c;某些注释和方法在JUnit 4和JUnit 5中具有相同的名称&#xff0c;并且当两组库依赖项都可用时&#xff0c;很容易导入错误的…
阅读更多...
最新文章

Copyright @ 2022~2023