【0】README
0.1)本文给出了平衡二叉树(AVL树)的插入例程涉及到的单旋转+双旋转的概念,并给出了代码实现;
0.2)本文源代码均为原创, 当然相关idea 还是借鉴人家的;(真心有点难,这个实现起来)
0.3) for detailed single rotate and double rotates , please visit http://blog.csdn.net/PacosonSWJTU/article/details/50522677
【1】AVL树
1.1)定义: AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Landis命名的。它是一种特殊的二叉查找树;
1.2)AVL树要求: 任一节点的左子树深度和右子树深度相差不超过1(空树高度定义为-1);
1.3)最简单的想法:要求左右子树具有相同的高度,这种想法并不强求树的深度要浅;
1.4)我们把必须重新平衡的节点叫做 α, 由于任意节点最多有两个儿子, 因此高度不平衡时, α 点的两颗子树的高度差2;
【2】AVL树的不平衡情况分析
2.1)AVL树的不平衡可能出现在下面四种情况:
- 1) 对α 的左儿子的左子树进行一次插入(左-左);
- 2) 对α 的左儿子的右子树进行一次插入(左-右);
- 3) 对α 的右儿子的左子树进行一次插入(右-左);
- 4) 对α 的右儿子的右子树进行一次插入(右-右);
2.2)对以上情况的Analysis:
- A1)上述情况中的 第1种 和 第4种情况 是插入发生在外部的情况(即左-左 or 右-右情况), 这种情况通过单旋转来处理;
- A2)上述情况中的 第2种 和 第3种情况 是插入发生在内部的情况(即左-右 or 右-左情况), 这种情况通过双旋转来处理;
2.3)单旋转(以图为荔枝)
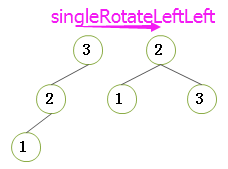
2.3.1)左-左情况的单旋转: 把树形象地看成是柔软灵活的,抓住节点2 , 使劲摇动它, 在重力作用下, 节点2 就变成了新树的根;二叉查找树的性质告诉我们: 在原树中,节点3大于节点2, 所以在新树中,节点3要从成为节点2 的右儿子;(后面的情况以此类推)
- Warning)要知道, 左左插入的情况下,不平衡树的左子树 或者有右孩子, 或者没有右孩子,但是我们在编程的时候,都要视为它有右孩子(因为即使算上,那也是NULL),所以首先要用 temp 来暂存不平衡树的左子树的右孩子, 最后还要把暂存的右孩子赋给根节点的左孩子(因为 不平衡树的左子树的所有节点值都小于不平衡树的根, 也顺便把不平衡树的左子树置空(可能的话));
- souce code as follows:
AVLTree singleRotateLeftLeft(AVLTree root) // the case is left-left
{AVLTree temp; AVLTree left; left = root->left;temp = left->right;left->right = root;root->left = temp;root->height = getHeight(root); return left;
}
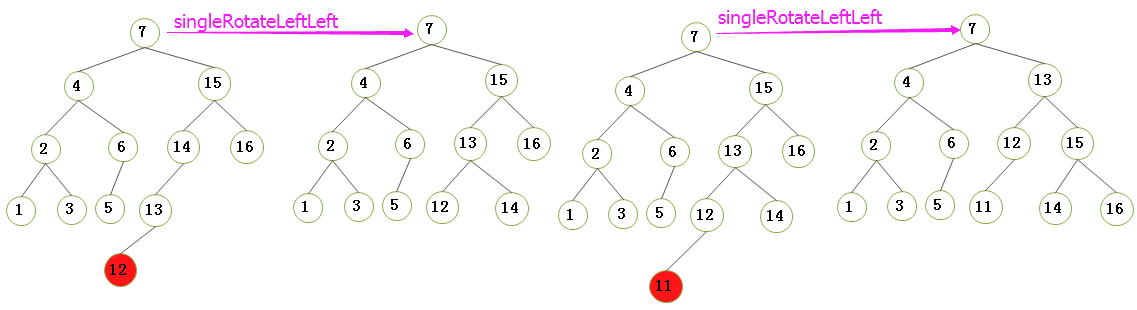
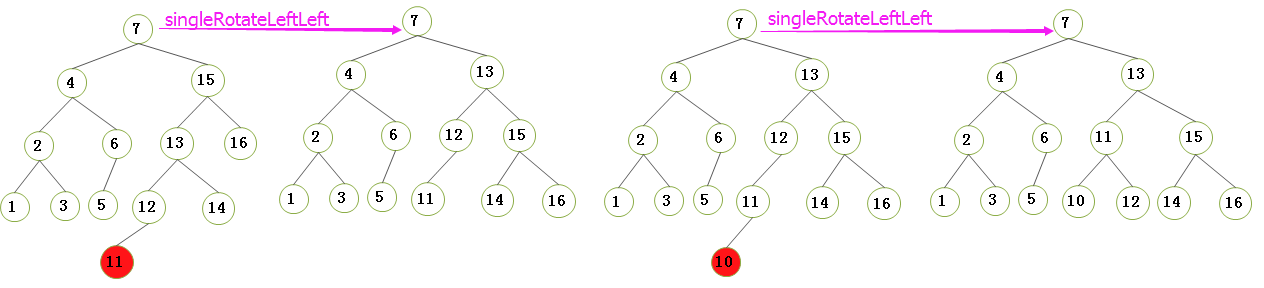
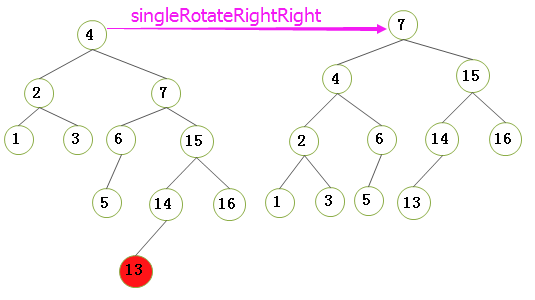
2.3.2)右-右情况的单旋转: 把树形象地看成是柔软灵活的,抓住节点4 , 使劲摇动它, 在重力作用下, 节点4 就变成了新树的根;二叉查找树的性质告诉我们: 在原树中,节点3小于节点4, 所以在新树中,节点4要从成为节点3 的左儿子;(后面的情况以此类推)
- Warning)要知道, 右插入的情况下,不平衡树的右子树 或者有左孩子, 或者没有左孩子,但是我们在编程的时候,都要视为它有左孩子(因为即使算上,那也是NULL),所以首先要用 temp 来暂存不平衡树的右子树的左孩子, 最后还要把暂存的左孩子赋给根节点的右孩子(因为 不平衡树的右子树的所有节点值都大于不平衡树的根, 也顺便把不平衡树的右子树置空(可能的话));
- souce code as follows:
AVLTree singleRotateRightRight(AVLTree root) // the case is right-right
{AVLTree temp; AVLTree right; right = root->right;temp = right->left;right->left = root;root->right = temp;root->height = max(getHeight(root->left), getHeight(root->right)) + 1; return right;
}
2.4)双旋转:
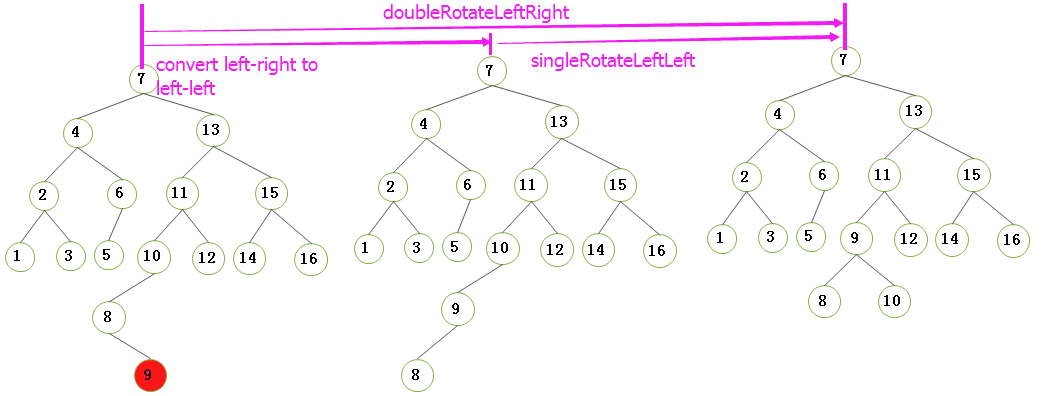
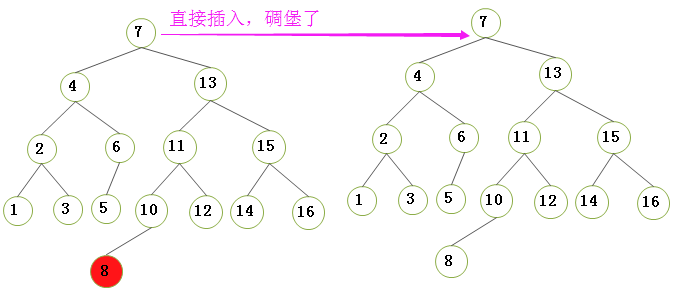
2.4.1)左-右情况的双旋转(我们以下图插入节点9为荔枝):也即是对于不平衡 节点10 的左儿子 节点8 的右子树NULL 进行一次插入节点9:
- step1)将 插入左儿子右子树的结构转换为 左儿子左子树的结构;
- step2)将 左儿子左子树的结构进行 左-左单旋转;
- souce code as follows:
AVLTree doubleRotateLeftRight(AVLTree root) // the case is left-right
{AVLTree temp;AVLTree right;temp = root->left;right = temp->right;root->left = right; // convert left-right into left-lefttemp->right = right->left;right->left= temp;temp->height = getHeight(temp);return singleRotateLeftLeft(root); // the case is left-left
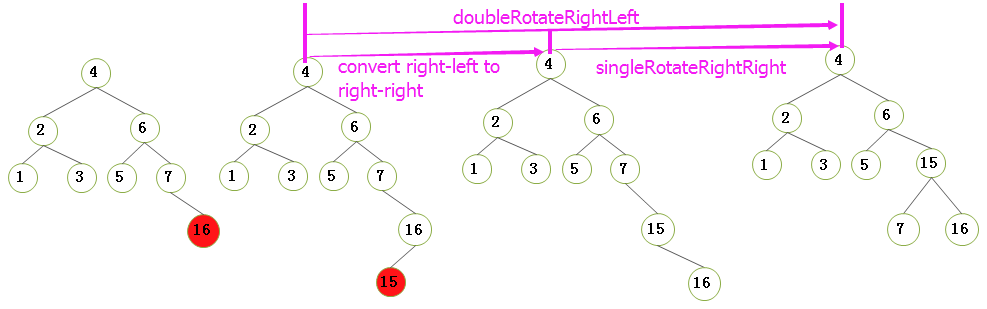
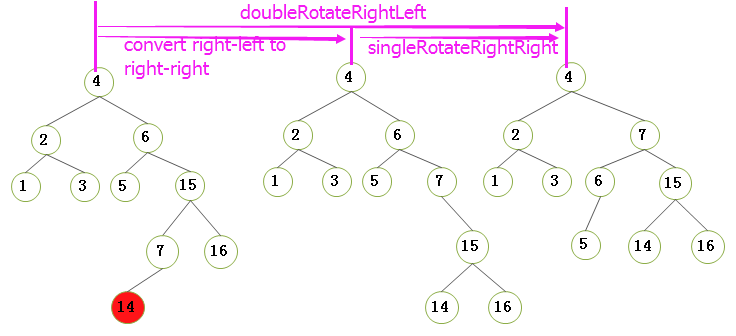
}2.4.2)右-左情况的双旋转(我们以下图插入节点15为荔枝):也即是对于不平衡 节点7 的右儿子 节点16 的左子树NULL 进行一次插入节点15:
- step1)将 插入右儿子左子树的结构转换为 右儿子右子树的结构;
- step2)将 右儿子右子树的结构进行 右-右单旋转;
souce code as follows:
AVLTree doubleRotateRightLeft(AVLTree root) // the case is right-left
{AVLTree temp;AVLTree left;temp = root->right;left = temp->left;root->right = left; // convert right-left into right-righttemp->left = left->right;left->right = temp;temp->height = getHeight(temp);return singleRotateRightRight(root); // the case is right-right
}
【3】source code
3.1)download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter4/p80_AVL_tree.c
3.2)source code at a glance :
#include <stdio.h>
#include <malloc.h>#define ElementType int
#define Error(str) printf("\n error: %s \n",str) struct AVLTree;
typedef struct AVLTree *AVLTree;AVLTree createAVLTree(ElementType);
AVLTree makeEmpty(AVLTree);
AVLTree insert(ElementType, AVLTree) ;
AVLTree deleteAVLTree(ElementType e, AVLTree root);
ElementType Retrieve(AVLTree);AVLTree singleRotateLeftLeft(AVLTree root);
AVLTree singleRotateRightRight(AVLTree root);
AVLTree doubleRotateLeftRight(AVLTree root);
AVLTree doubleRotateRightLeft(AVLTree root);int getHeight(AVLTree root);// we adopt child-sibling notation
struct AVLTree
{ElementType value;AVLTree left;AVLTree right;int height;
};
//get the maximum
int max(int a, int b)
{return a > b ? a : b;
}// get the height
int getHeight(AVLTree root)
{if(!root)return -1;elsereturn 1 + max(getHeight(root->left), getHeight(root->right));
}// create a AVLTree with root node
AVLTree createAVLTree(ElementType value)
{ AVLTree t;t = (AVLTree)malloc(sizeof(struct AVLTree));if(!t) {Error("out of space, from func createAVLTree"); return NULL;} t->left = NULL;t->right = NULL; t->value = value;t->height = 0;return t;
}// make the AVLTree empty
AVLTree makeEmpty(AVLTree t)
{if(t){makeEmpty(t->left);makeEmpty(t->right); free(t);} return NULL;
}AVLTree doubleRotateLeftRight(AVLTree root) // the case is left-right
{AVLTree temp;AVLTree right;temp = root->left;right = temp->right;root->left = right; // convert left-right into left-lefttemp->right = right->left;right->left= temp;temp->height = getHeight(temp);return singleRotateLeftLeft(root); // the case is left-left
}AVLTree doubleRotateRightLeft(AVLTree root) // the case is right-left
{AVLTree temp;AVLTree left;temp = root->right;left = temp->left;root->right = left; // convert right-left into right-righttemp->left = left->right;left->right = temp;temp->height = getHeight(temp);return singleRotateRightRight(root); // the case is right-right
}AVLTree singleRotateLeftLeft(AVLTree root) // the case is left-left
{AVLTree temp; AVLTree left; left = root->left;temp = left->right;left->right = root;root->left = temp;root->height = getHeight(root); return left;
}AVLTree singleRotateRightRight(AVLTree root) // the case is right-right
{AVLTree temp; AVLTree right; right = root->right;temp = right->left;right->left = root;root->right = temp;root->height = max(getHeight(root->left), getHeight(root->right)) + 1; return right;
}AVLTree insert(ElementType e, AVLTree root)
{ if(!root) {// find the node with its left or right being NULLroot = createAVLTree(e);if(root) return root; else return NULL;}if(e > root->value) { root->right = insert(e, root->right); if(getHeight(root->right) - getHeight(root->left) == 2) { // after insertion, we should judge whether the tree is balanced or notif(e > root->right->value) // the case is right-rightroot = singleRotateRightRight(root);else // the case is right-leftroot = doubleRotateRightLeft(root);}}else if(e < root->value) { root->left = insert(e, root->left); if(getHeight(root->left) - getHeight(root->right) == 2) { // after insertion, we should judge whether the tree is balanced or notif(e < root->left->value) // the case is left-leftroot = singleRotateLeftLeft(root);else // the case is left-rightroot = doubleRotateLeftRight(root);}}elseError(" you cannot insert the node into the tree for its value equals to one in the tree"); root->height = max(getHeight(root->left), getHeight(root->right)) + 1; // after insertion, root's height increses one layerreturn root; // dont't forget this line !
} // analog print directories and files name in the AVLTree, which involves postorder traversal.
void printPreorder(int depth, AVLTree root)
{ int i;if(root) { for(i = 0; i < depth; i++)printf(" "); printf("%d\n", root->value);printPreorder(depth + 1, root->left); printPreorder(depth + 1, root->right); // Attention: there's difference between traversing binary tree and common tree }else {for(i = 0; i < depth; i++)printf(" "); printf("NULL\n");}
} int main()
{AVLTree root; printf("\n ====== test for building the AVLTree ====== \n"); printf("\n [the left-left case] test for creating a AVL tree with inserting 3, 2, 1 in trun \n"); root = NULL;root = insert(3, root); root = insert(2, root); root = insert(1, root); printPreorder(1, root); printf("\n [the right-right case] test for inserting node '4' and '5' in turn \n"); insert(4, root);insert(5, root);printPreorder(1, root); printf("\n [the right-right case] test for inserting node '6 in turn \n"); root = insert(6, root); printPreorder(1, root); printf("\n [the right-right case] test for inserting node '7' and '16' in turn \n"); root = insert(7, root);root = insert(16, root);printPreorder(1, root); printf("\n [the right-left case] test for inserting node '15' in turn \n"); root = insert(15, root); printPreorder(1, root); printf("\n [the right-left case] test for inserting node '14' in turn \n"); root = insert(14, root); printPreorder(1, root); printf("\n [the right-left case] test for inserting node '13' in turn \n"); root = insert(13, root); printPreorder(1, root); printf("\n [the left-left case] test for inserting node '12' in turn \n"); root = insert(12, root); printPreorder(1, root); printf("\n [the left-left case] test for inserting node '11' and '10' in turn \n"); root = insert(11, root); root = insert(10, root); printPreorder(1, root); printf("\n [the left-left case] test for inserting node '8' in turn \n"); root = insert(8, root); printPreorder(1, root); printf("\n [the left-right case] test for inserting node '9' in turn \n"); root = insert(9, root); printPreorder(1, root); return 0;
}
【4】printing result set
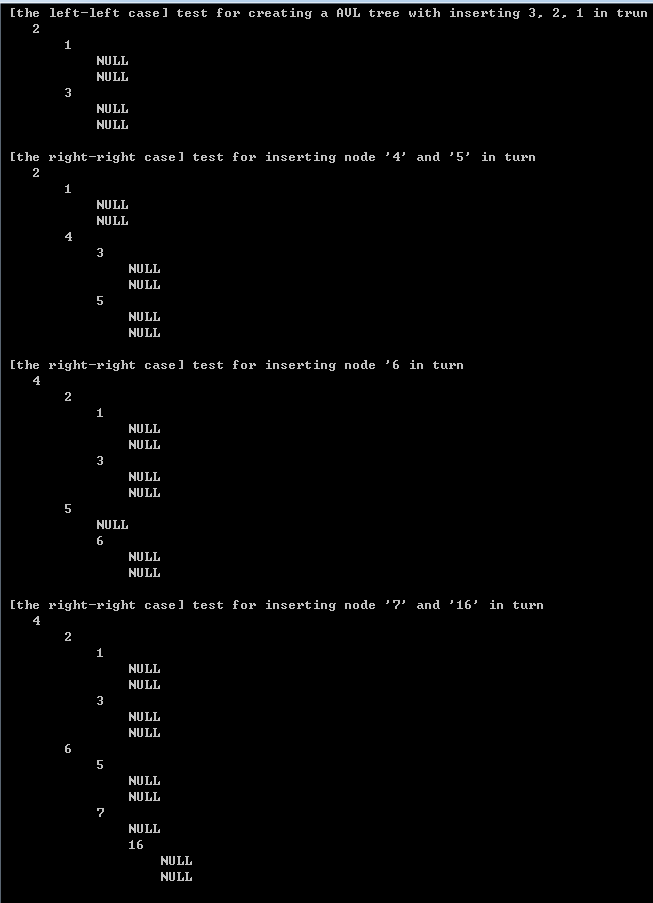
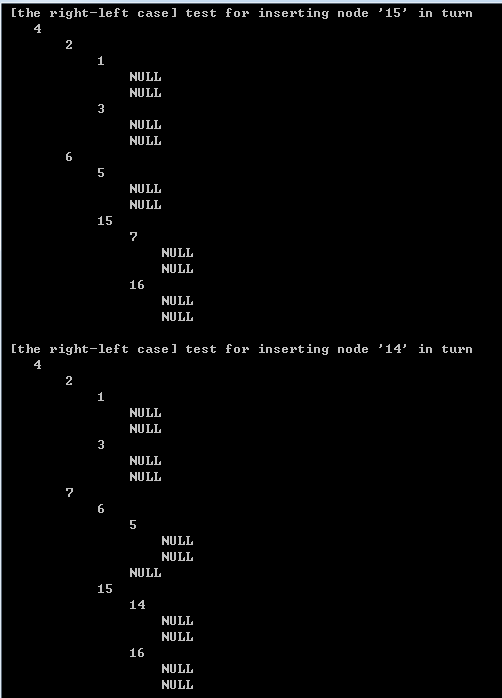
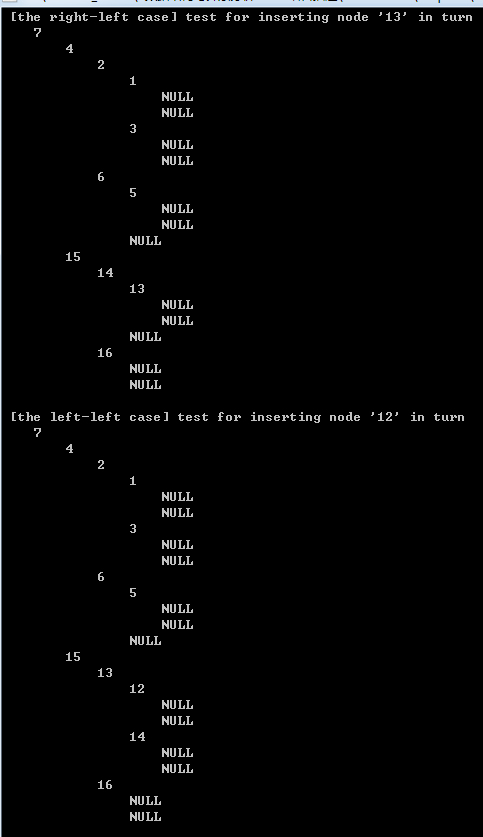



)










)




)

的快捷键/终端快捷键)