【0】README
0）本文旨在给出 快速排序 的 源码实现和源码分析（分析它的坑）；
2）要知道 在 元素个数小于10的时候，快速排序不如插入排序；注意快速排序选取枢纽元 时 所使用的方法是 三数中值分割法，截止范围为10（也就是，如果排序的数组个数小于10， 就不选择快速排序， 而是选择其他排序方法， 如希尔排序或插入排序）；（不能再干货）
3）因为 快速排序是基于分治的，这里通过递归实现了分治，每次递归后，待排序的元素个数都会减少，所以最后都是通过插入排序来完成排序的；
4）快速排序基础 参见http://blog.csdn.net/pacosonswjtu/article/details/48879419， 插入排序基础参见 http://blog.csdn.net/pacosonswjtu/article/details/48879263
Attention）小生的插入排序以 本文中的 插入排序为准，以前写的都不算数（哈哈），因为我发现这个 版本的插入排序太 tm 灵活了，仅此而已；
5）快速选择算法（从n个数中选择第k个最大（小）数），代码实现在文末；快速选择算法 基础知识 参见 http://blog.csdn.net/pacosonswjtu/article/details/48915197
【1】上源码
#include <stdio.h>
#include <malloc.h>#define ElementType intvoid swap(ElementType* a, ElementType* b);
ElementType median3(ElementType* array, int left, int right);
void quicksort(ElementType* array, int left, int right);
void printArray(ElementType* array, int N);
void insertionSort(ElementType* array, int left, int right);// swap array arraynd b.
void swap(ElementType* array, ElementType* b)
{ElementType t;t=*array;*array=*b;*b=t;
}// 3数中值分割法 选出 left center right 分别存储最小，中间，最大值
// 然后 将中位数隐藏到倒数第2个元素
ElementType median3(ElementType* array, int left, int right)
{ int center = (left+right)/2;if(array[left]>array[center]){swap(&array[left], &array[center]); }if(array[left]>array[right]){swap(&array[left], &array[right]); }if(array[center]>array[right]){swap(&array[center], &array[right]); }/* 将中位数隐藏到倒数第2个元素 */swap(&array[center], &array[right-1]);return array[right-1];
}/* 快速排序 */
void quicksort(ElementType array[], int left, int right)
{int i, j;ElementType pivot; // 枢轴.// if(right-left >= 10) { also you can let lower limit be 10.if(right-left >= 3) { /* rihgt-left>=3,才有三数中值分割法的应用 *//* 三数分割 median3 把最大元放入array[right]了，枢纽元放入array[right-1]，最小元放入array[left] */pivot = median3(array, left, right); i = left; //i 指向最小元.j = right-1; // j 指向枢纽元.for(;;) {while(array[++i] < pivot); /* (这里必须++i, 不能i++)找大元素，i停在那里,i起始从 left+1 */while(array[--j] > pivot); /* (这里必须--j, 不能j--)找小元素，j停在那里,j起始从 right-2 */if(i<j){swap(&array[i], &array[j]); /* 分割结束 */}else{break;}}//key: array[i]最后指向大元素，array[right-1]指向枢纽元，将它们交换； swap(&array[i], &array[right-1]); // 交换后, array[i]=枢纽元, 前面的元素小于它, 后面的元素大于它.quicksort(array, left, i-1); /* 递归进行快速排序 */quicksort(array, i+1, right); /* 递归进行快速排序 */} else /* 当数组长度小于cutoff-隔断距离的话，那么就采用插入排序，因为这样效率高些*/{insertionSort(array, left, right);}
}// 插入排序
void insertionSort(ElementType* array, int left, int right)
{int i, j;ElementType temp; for(i=left+1; i<=right; i++) // 下标i 存储无序部分的第一个元素，即下标i-1 存储有序的最后一个元素.{temp = array[i];for(j=i-1; j>=left; j--) // 下标j 初始存储有序部分的最后一个元素，并在有序部分逆向滑动.{if(temp < array[j]){array[j+1] = array[j];}else{break;}}array[j+1] = temp; // who not array[j]? 因为j--执行后 才推出了循环，所以要加回去.}
}/* 打印数组数据 */
void printArray(int* array, int size)
{int i;for(i=0; i<size; i++){printf("%d ", array[i]);}printf("\n");
}#include "p177_quick_sort.h"int main()
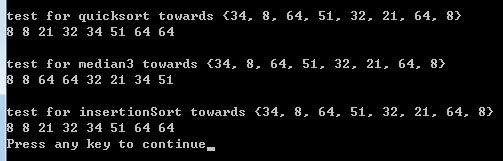
{ElementType array[] = {34, 8, 64, 51, 32, 21, 64, 8};ElementType array2[] = {34, 8, 64, 51, 32, 21, 64, 8};ElementType array3[] = {34, 8, 64, 51, 32, 21, 64, 8};int size=8; // test for quicksort.printf("\ntest for quicksort towards {34, 8, 64, 51, 32, 21, 64, 8}\n");quicksort(array, 0, size-1);printArray(array, size); // test for median3printf("\ntest for median3 towards {34, 8, 64, 51, 32, 21, 64, 8}\n");median3(array2, 0, size-1);printArray(array2, size);// test for insertionSortprintf("\ntest for insertionSort towards {34, 8, 64, 51, 32, 21, 64, 8}\n");insertionSort(array3, 0, size-1);printArray(array3, size);
}
【2】review 插入排序代码实现（注意我的输入参数，可能和他家的不一样）
1）参数分析：这个插入排序的源码荔枝 比较灵活，因为输入参数可变，不一定非得认为 left==0，还可以对其子数组进行插入排序；
// 插入排序
void insertionSort(ElementType* array, int left, int right)
{int i, j;ElementType temp; for(i=left+1; i<=right; i++) // 下标i 存储无序部分的第一个元素，即下标i-1 存储有序的最后一个元素.{temp = array[i];for(j=i-1; j>=left; j--) // 下标j 初始存储有序部分的最后一个元素，并在有序部分逆向滑动.{if(temp < array[j]){array[j+1] = array[j];}else{break;}}array[j+1] = temp; // who not array[j]? 因为j--执行后 才推出了循环，所以要加回去.}
}
【3】快速选择算法
1）intro：快速选择算法是从n个数中选择第k个最大（小）数算法，且是快速排序的变体算法，因为快速排序基于递归的分治算法，每轮递归后，都可以确定枢纽元的最终下标位置；所以通过 k 次 快速排序就可以确定 第k 个 最大（小）元素了，而不用对所有 元素进行排序；
2）当元素个数小于10（官方建议取10，不过这里的测试用例取3）的时候：快速排序依然会用到插入排序；
3）快速选择算法分析：快速选择算法 是 快速排序的变体算法，基本的idea是一样的，只不过 快速选择函数 多带了一个输入参数 k值，且在函数末尾要比较 i（因为 array[i] 存储着枢纽值） 和 k的大小以此来确定 该在哪个 数组范围内递归进行快速选择，代码如下：
#include <stdio.h>
#include <malloc.h>#define ElementType int
#define Error(str) printf("\nerror: %s", str)void swap(ElementType* a, ElementType* b);
ElementType median3(ElementType* array, int left, int right);
void quickselect(ElementType* array, int left, int right, int k);
void printArray(ElementType* array, int N);
void insertionSort(ElementType* array, int left, int right);// swap array arraynd b.
void swap(ElementType* array, ElementType* b)
{ElementType t;t=*array;*array=*b;*b=t;
}// 3数中值分割法 选出 left center right 分别存储最小，中间，最大值
// 然后 将中位数隐藏到倒数第2个元素
ElementType median3(ElementType* array, int left, int right)
{ int center = (left+right)/2;if(array[left]>array[center]){swap(&array[left], &array[center]); }if(array[left]>array[right]){swap(&array[left], &array[right]); }if(array[center]>array[right]){swap(&array[center], &array[right]); }/* 将中位数隐藏到倒数第2个元素 */swap(&array[center], &array[right-1]);return array[right-1];
}/* 快速选择(第k+1个最大元素), 所以如果要选择第k个最大元素，main函数需要传入k-1 */
void quickselect(ElementType array[], int left, int right, int k)
{int i, j;ElementType pivot; // 枢轴.if(k>right){Error("failed quickselect() for k is greater than right.");return;}// if(right-left >= 10) { also you can let lower limit be 10.if(right-left >= 3) { /* rihgt-left>=3,才有三数中值分割法的应用 *//* 三数分割 median3 把最大元放入array[right]了，枢纽元放入array[right-1]，最小元放入array[left] */pivot = median3(array, left, right); i = left; //i 指向最小元.j = right-1; // j 指向枢纽元.for(;;) {while(array[++i] < pivot); /* (这里必须++i, 不能i++)找大元素，i停在那里,i起始从 left+1 */while(array[--j] > pivot); /* (这里必须--j, 不能j--)找小元素，j停在那里,j起始从 right-2 */if(i<j){swap(&array[i], &array[j]); /* 分割结束 */}else{break;}}//key: array[i]最后指向大元素，array[right-1]指向枢纽元，将它们交换； swap(&array[i], &array[right-1]); // 交换后, array[i]=枢纽元, 前面的元素小于它, 后面的元素大于它.// 上面的代码和快速排序一样，下面的代码用于基于递归的快速选择if(k > i) {quickselect(array, i+1, right, k); }else if(k < i){quickselect(array, left, i-1, k); }// else k == i, bingo. } else /* 当数组长度小于3(10)的话，那么就采用插入排序，因为这样效率高些*/{insertionSort(array, left, right);}
}// 插入排序
void insertionSort(ElementType* array, int left, int right)
{int i, j;ElementType temp; for(i=left+1; i<=right; i++) // 下标i 存储无序部分的第一个元素，即下标i-1 存储有序的最后一个元素.{temp = array[i];for(j=i-1; j>=left; j--) // 下标j 初始存储有序部分的最后一个元素，并在有序部分逆向滑动.{if(temp < array[j]){array[j+1] = array[j];}else{break;}}array[j+1] = temp; // who not array[j]? 因为j--执行后 才推出了循环，所以要加回去.}
}/* 打印数组数据 */
void printArray(int* array, int size)
{int i;for(i=0; i<size; i++){printf("%d ", array[i]);}printf("\n");
}#include "p185_quick_select.h"int main()
{ElementType array[] = {34, 8, 64, 51, 32, 21, 64, 8,35, 9, 65, 50, 31, 20, 63, 8}; int size=16; int k = 6;// test for quickselect.printf("\ntest for quickselect towards {34, 8, 64, 51, 32, 21, 64, 8, 35, 9, 65, 50, 31, 20, 63, 8}\n");quickselect(array, 0, size-1, k-1); // pass k-1 not k, you know it.printf("\nthe %dth maximum element is %d \n", k, array[k-1]);
}
:java类的加载机制)