【0】README

1）本文旨在 介绍 ReviewForJob——深度优先搜索的应用 及其 源码实现 ；

2）搜索树的技术分为广度优先搜索 和 深度优先搜索：而广度优先搜索，我们前面利用 广度优先搜索计算无权最短路径已经做过分析了，有兴趣的可以参考 广度优先搜索相关

3）图经过 深度优先搜索后会生成多个 树：这种树叫深度优先树，要知道多个 深度优先树就组合成了深度优先森林了；

4）深度优先搜索的应用有： 

4.1）基于无向图的dfs应用：遍历无向图，查找无向图的割点和背向边（双连通性）；

4.2）基于有向图的dfs应用：遍历有向图，查找强分支 等， 下面一一对 dfs的 应用荔枝进行分析；

4.3）其中查找无向图的割点和背向边 是 核心知识，后面查找强分支会基于 割点和背向边进行分析；遍历有向图和 遍历无向图 是 dfs 应用的最基础的荔枝，且他们的遍历方式 大致差不多，因为 dfs 就是相当于 对树的先序遍历；

【1】深度优先搜索基础（depth first search——DFS）

1）图的深度优先搜索遍历（DFS）类似于二叉树的先序遍历。它的基本思想是(steps）： 

step1）首先访问出发点v， 并将其标记为已访问过；

step2）然后选取与v 邻接的未被访问的任意一个顶点w ， 并访问它；

step3）再选取与w 邻接的未被访问的任一顶点并访问它， 依次重复进行；

step4）当一个顶点所有的邻接顶点都被访问过时， 则依次退回到最近被访问过的顶点（这里就是一个递归访问的过程）， 若该顶点还有其他邻接顶点未被访问， 则从这些未被访问的顶点中取一个重复上述的访问过程， 直至图中所有顶点都被访问过为止；

2）dfs的应用——遍历无向图的荔枝 dfs 遍历无向图源码

// 以下数组的 0 号下标 通通不用。
int visited[VertexNum+1]; // 顶点被访问状态 visited[i]==1|0(已访问|未访问)
int num[VertexNum+1]; // 顶点被访问的序号.
int parent[VertexNum+1]; // parent[i]=j 表明 顶点i 紧跟着顶点j之后 被访问.
int counter=0; // 已被访问的顶点数量.// dfs 深度优先搜索算法.
// 邻接表adjList(图的标准表示方法)，vertexIndex 顶点索引，depth 用于打印空格，visted数组 用于存储 顶点访问状态.
void dfs_undirected_graph(AdjList adjList, int vertex, int depth) // step1: 从vertex 触发.
{int i;Vertex temp = adjList->array[vertex-1];int adjVertex;visited[vertex] = 1; // step1: 更新vertex 顶点为 已访问状态.num[vertex] = ++counter; // 顶点vertex 被访问的序号.	while(temp->next) // step2: 遍历 vertex顶点的 邻接顶点.{adjVertex = temp->next->index;		if(!visited[adjVertex]) // step2: 邻接顶点没有被访问过, 则利用dfs 进行访问.{parent[adjVertex] = vertex;			// just for printing effectfor(i = 0; i < depth; i++)  printf("           ");printf("v[%c]->v[%c] (build edge)\n", vertex+64, adjVertex+64); // 都说了是先序遍历, 记录函数在 dfs递归之前.dfs_undirected_graph(adjList, adjVertex, depth+1); // 递归dfs}				temp = temp->next;} 
} 

【2】dfs的应用——双连通性 dfs应用——双连通性源码

0）双连通性： 如果一个连通的无向图中的任意一个顶点删除后，剩下的图仍然是连通的，那么这样的无向图就是双连通的；

1）看几个定义：

定义1）背向边(backside)： 当我们处理（v, w）时，发现 w 已被标记，并且当我们处理 (w, v) 时 发现v 已被标记，那么我们就画一条虚线，并称之为 背向边；

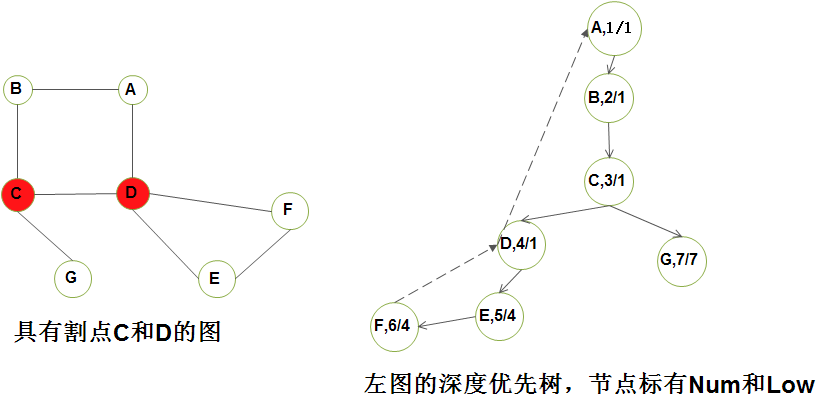
定义2）割点(articulation)：如果一个图不是双连通的，那么将其删除后将不在连通的那些顶点叫做割点；下面的图片中C 和 D 就是割点；

2）如何寻找背向边？ 这可是个大活：

你要想1）我们看看 (D, A) 和 (F, D) 为什么是背向边？ 看看 dfs 的遍历顺序，A->B->C->D， 遍历到D后，D开始遍历它的邻接顶点，D会遍历A 发现 A已经被访问过了； 之后当 dfs 递归算法 回溯到 顶点A 的时候，A 遍历邻接顶点D ，发现D被 访问过了，所以可以确认（D,A）就是背向边；为什么这么说，下面给出代码的调试信息：

// 下列数组 0 号下标通通不用.
int visited[VertexNum+1]; // 顶点被访问状态 visited[i]==1|0(已访问|未访问)
int num[VertexNum+1]; // 顶点被访问的序号.
int parent[VertexNum+1]; // parent[i]=j 表明 顶点i 紧跟着顶点j之后 被访问.
int low[VertexNum+1]; // low[i]=j 表明 顶点i 可以访问(包括通过背向边)的最先被访问的顶点是顶点j.
int counter=0; // 已被访问的顶点数量.// dfs 深度优先搜索算法.用于寻找背向边和割点.
// 邻接表adjList(图的标准表示方法)，vertexIndex 顶点索引，depth 用于打印空格
void dfs_find_articulation(AdjList adjList, int vertex, int depth)
{int i;Vertex temp = adjList->array[vertex-1];int adjVertex;visited[vertex] = 1; // 更新vertex 顶点为 已访问状态. vertex 从1开始取，所以减1.low[vertex] = num[vertex] = ++counter; // 顶点vertex 被访问的序号.	while(temp->next){adjVertex = temp->next->index;		if(!visited[adjVertex]) // 邻接顶点没有被访问过, 则利用dfs 进行访问.{parent[adjVertex] = vertex;			// just for printing effectfor(i = 0; i < depth; i++)  printf("           ");printf("v[%c]->v[%c] (build edge) (%c, %d/%d)\n", vertex+64, adjVertex+64, vertex+64, num[vertex], low[vertex]);dfs_find_articulation(adjList, adjVertex, depth+1);if(low[adjVertex] >= num[vertex]) // 判断 vertex是否是割点.{// just for printing effectfor(i = 0; i < depth; i++)  printf("           ");printf("%c is an articulation point for (low[%c]=%d) >= (num[%c]=%d)\n", vertex+64, adjVertex+64, low[adjVertex], vertex+64, num[vertex]);}low[vertex] = min(low[vertex], low[adjVertex]); // 基于后序遍历更新low[].}	else // 邻接顶点被访问过.{						if(parent[vertex] != adjVertex) // true，则(vertex, adjVertex)就是背向边{low[vertex] = min(low[vertex], num[adjVertex]); // 更新 当前节点i的low[i]				// just for printing effect, 不作为算法的一部分.for(i = 0; i < depth; i++)  printf("           ");	// 不作为算法的一部分over.printf("v[%c]->v[%c] (backside) (%c, %d/%d)\n", vertex+64, adjVertex+64, vertex+64, num[vertex], low[vertex]);				} 			 			 }				temp = temp->next;} 
} 

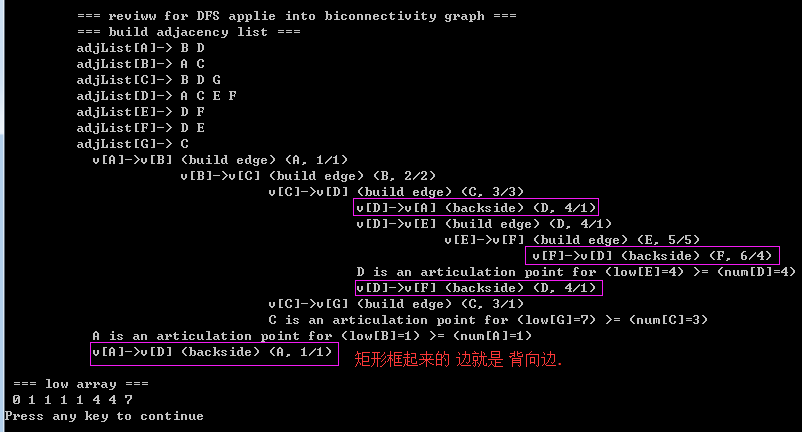
对上面的源码和打印结果图的分析（Analysis）

A1）从结果图中看出， 背向边有4条，错误！其实只有2条。我们只看（D,A）这条。 当 D 遍历A的时候，产生背向边，而当 A遍历D的时候产生背向边；但它们是同一条边；那如何 记录 背向边呢？ 要知道 背向边的起点是后访问的节点，终点是先访问的节点，也就是说 当 num[vertex] > num[adjVertex] (vertex, adjVertex) 才是背向边；背向，背向，你就当它是逆向的意思就行啦！

A2）为什么41行的 条件语句就可以判断 （vertex,adjVertex）就是背向边？ 要知道 parent数组记录的是 上一个访问的顶点，如 parent[i]=j 则表示 在迭代i 之前访问的顶点是 顶点j。 因为 如果 顶点 adjVertex 恰好先于 顶点vertex 被访问的话，第21行的代码不满足，程序跳转到41行执行。如果没有 41行的条件语句做判断，就会认为 相邻两个被访问的顶点（num[i] - num[j] ==1）组成的边（i,j）是 背向边，这样显然是不行。（因为相邻被访问的顶点不可能是背向边，参见上面的深度优先树），那所以要排除这种case，加上了if 条件语句；

2）分析low数组： low[i]=j 表明 low[i]记录的是 当前顶点i 可以访问（包括通过背向边）的最先被访问的顶点是顶点j；看上面 的深度优先树，（D,A）是背向边，low[D]=1，因为它可以访问到 A，而num[A]=1；同时你也看到了 low[C]=1 也等于1，因为后序遍历更新了 其 low值。什么叫后序遍历？ 后序的意思就是 更新动作在 dfs 递归函数之后执行；参见37行；

3）如何更新low？ 要知道 low[v] 取值有三种：

case1）num[v]：第17行代码

case2）所有背向边(v,w) 中的最低num(w); 第43行代码；通过背向边可以访问的顶点的num最小值（越先被访问，值就越小）；

case3）树的所有边(v, w) 中的最低 low(w)；第37行代码；这里就是一个 dfs 回溯的 更新 low值了，比如 C 访问D， D 访问A，D的low值会更新为1，当D 被访问完后，会回溯到C，由于第37行的更新low值是后序，所以 low[C] 会 和 low[D] 做比较并选取最小值，同时dfs继续回溯到B.......；就是这个样子的；（开心）

4）如何查找割点？

4.1）割点肯定有大于等于2个的邻接顶点；

4.2）某个顶点是割点当且仅当它有某个儿子 w 使得 low(w) >= num(v)；参见顶点C 和 顶点D；第30行代码用于判断割点；

【3】dfs应用——遍历有向图 dfs 应用遍历有向图源码

1）intro：利用dfs 遍历有向图，其idea 同 dfs 遍历无向图相同；大致的steps 如下：

step1）选取任意一个未被访问的顶点为起点，进行dfs；

step2）待dfs 执行完后，可能还有一些节点无法通过一次dfs 遍历到的（因为图可能是非强连通的），这时就需要选取任意一个未被访问的顶点作为起点，继续dfs，返回step1；

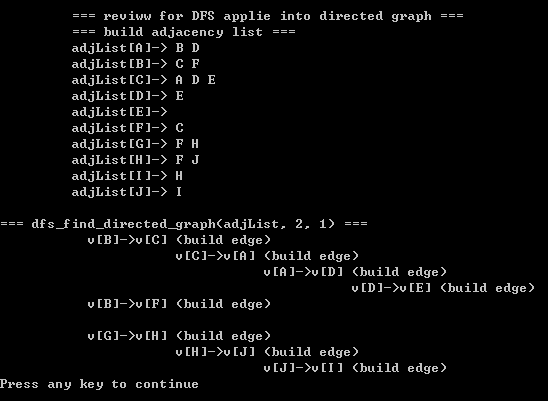
// 使用 dfs 遍历有向图.printf("\n=== dfs_find_directed_graph(adjList, 1, 1) ===\n");dfs_find_directed_graph(adjList, 2, 1);	 // step1:for(i=1; i<=VertexNum; i++) // step2:{if(!visited[i]){printf("\n");dfs_find_directed_graph(adjList, i, 1);}}

2）基于dfs 遍历有向图的源码如下：（与遍历无向图差不了多少）

#define VertexNum 10int min(int a, int b);// 0 号下标通通不用.
int visited[VertexNum+1]; // 顶点被访问状态 visited[i]==1|0(已访问|未访问)
int num[VertexNum+1]; // 顶点被访问的序号.
int parent[VertexNum+1]; // parent[i]=j 表明 顶点i 紧跟着顶点j之后 被访问.
int low[VertexNum+1]; // low[i]=j 表明 顶点i 可以访问(包括通过背向边)的最先被访问的顶点是顶点j.
int counter=0; // 已被访问的顶点数量.// dfs 深度优先搜索算法. 遍历有向图.
// 邻接表adjList(图的标准表示方法)，vertexIndex 顶点索引，depth 用于打印空格
void dfs_find_directed_graph(AdjList adjList, int vertex, int depth)
{int i;Vertex temp = adjList->array[vertex-1];int adjVertex;visited[vertex] = 1; // 更新vertex 顶点为 已访问状态. vertex 从1开始取，所以减1.low[vertex] = num[vertex] = ++counter; // 顶点vertex 被访问的序号.	while(temp->next){adjVertex = temp->next->index;		if(!visited[adjVertex]) // 邻接顶点没有被访问过, 则利用dfs 进行访问.{parent[adjVertex] = vertex;			// just for printing effectfor(i = 0; i < depth; i++)  printf("           ");printf("v[%c]->v[%c] (build edge) \n", vertex+64, adjVertex+64);dfs_find_directed_graph(adjList, adjVertex, depth+1);low[vertex] = min(low[vertex], low[adjVertex]); // 基于后序遍历更新low[].}	else // if(visited[adjVertex-1]) 邻接顶点被访问过.{			if(parent[vertex] != adjVertex) // true，则(vertex, adjVertex)就是背向边{low[vertex] = min(low[vertex], num[adjVertex]); // 更新 当前节点i的low[i]// just for printing effect, 不作为算法的一部分.for(i = 0; i < depth; i++)  printf("           ");	printf("v[%c]->v[%c] (backside)\n", vertex+64, adjVertex+64);// 不作为算法的一部分over.} 			 			 }				temp = temp->next;} 	
} int min(int a, int b)
{return a>b? b:a;
}

补充）深度优先搜索的一种用途是： 检测一个 有向图是否是无圈图。法则如下：一个有向图是无圈图当且仅当它没有背向边；（这个法则，本文的章节【2】有叙述）；ps： 拓扑排序也可以用来确定一个图是否是无圈图；

【4】dfs应用——查找强分支 dfs应用——查找强分支源码

1）intro：通过执行两次深度优先搜索，我们可以检测一个有向图是否是强连通的，如果它不是强连通的，那么可以得到顶点的一些子集（强连通子图 或 强分支）；

2）由于要选取 最大的 num[i]， 所以用到了二叉堆优先队列，首先将 num[] 数组元素插入大根堆，然后再 deleteMin() 删除最小元素 选取 最大的 num[i]；

3）基于 dfs 查找强分支 的 算法描述

step1）在有向图G 上执行 dfs 形成深度优先生成森林，通过对 深度优先生成森林的后序遍历将 G中顶点的访问顺序编号（用 num[] 数组记录其访问序号）；

// 使用 dfs 查找强连通分支.// step1: 基于dfs 遍历 有向图G，对顶点的访问顺序编号.printf("\n=== dfs_find_directed_graph(adjList, 2, 1) ===\n");dfs_find_strong_component(adjList, 2, 1);	 // start=1.for(i=1; i<=VertexNum; i++){if(!visited[i]){printf("\n");dfs_find_strong_component(adjList, i, 1);}}// step1 over.

step2）把G的所有边反向，形成 Gr（reverse）；

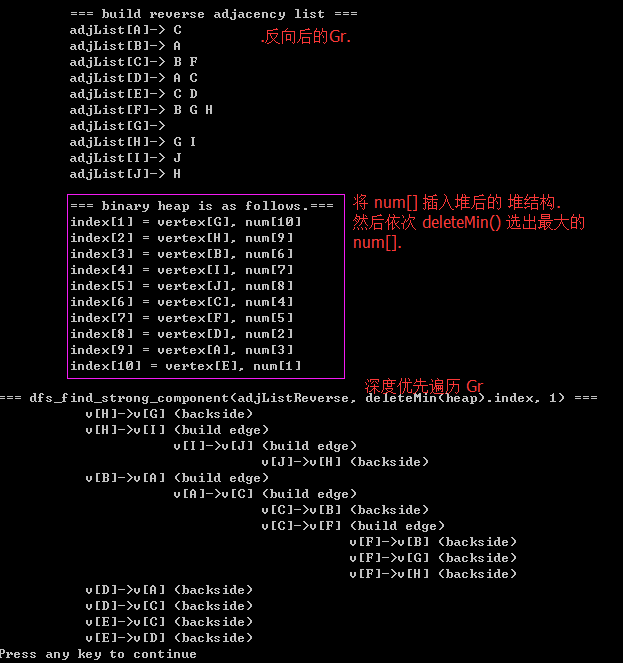
//step2: 把G的所有边反向 -> Gr.adjListReverse = init(capacity);	if(adjListReverse==NULL){return;}				printf("\n\t === build reverse adjacency list ===\n");for(i=0;i<row;i++){			for(j=0; j<col; j++){if(adjArray[i][j]){insertAdjList(adjListReverse, adjArray[i][j]-1, i+1, adjArray[i][j]); // 插入节点到邻接表.(无向图权值为全1)}}} // step2 over.

step3）从编号最大的顶点开始，依次进行基于 dfs 的 有向图遍历，每次遍历的起点都作为 强连通子图（强分支）的根；

// step3: 从序号最大的顶点开始，依次对Gr 进行 dfs.（这里需要建立一个大根堆）	// step3.1: 利用num[] 建立大根堆heap = initBinaryHeap(VertexNum+1); // 因为0号下标不用.for(i=1; i<=VertexNum; i++){insert(createHeapNode(i, num[i]), heap);// 初始化数组为0visited[i] = 0;num[i] = 0;				parent[i] = 0;	} // step3.1 over.printf("\n\t === binary heap is as follows.===");printBinaryHeap(heap);counter=0; // 初始化count=0；// step3.2 依次选取 最大序号的顶点进行dfsprintf("\n=== dfs_find_strong_component(adjListReverse, deleteMin(heap).index, 1) ===\n");while(!isEmpty(heap) && counter!=VertexNum){			vertex = deleteMin(heap).index; // 依次选取 最大访问序号的顶点.		if(!visited[vertex]) // 如果该顶点没有被访问的话.{dfs_find_strong_component(adjListReverse, vertex, 1);}		}

step4）在该深度优先生成森林中的每棵树 都形成一个强连通分支；

4）源码如下

#define VertexNum 10int min(int a, int b);// 0 号下标通通不用.
int visited[VertexNum+1]; // 顶点被访问状态 visited[i]==1|0(已访问|未访问)
int num[VertexNum+1]; // 顶点被访问的序号.
int parent[VertexNum+1]; // parent[i]=j 表明 顶点i 紧跟着顶点j之后 被访问.
int counter=0; // 已被访问的顶点数量.// dfs 深度优先搜索算法.
// 邻接表adjList(图的标准表示方法) , vertex 顶点索引，depth 用于打印空格
void dfs_find_strong_component(AdjList adjList, int vertex, int depth)
{int i;Vertex temp = adjList->array[vertex-1];int adjVertex;visited[vertex] = 1; // 更新vertex 顶点为 已访问状态. vertex 从1开始取，所以减1.	while(temp->next){adjVertex = temp->next->index;		if(!visited[adjVertex]) // 邻接顶点没有被访问过, 则利用dfs 进行访问.{			parent[adjVertex] = vertex;	// just for printing effectfor(i = 0; i < depth; i++)  printf("           ");printf("v[%c]->v[%c] (build edge) \n", vertex+64, adjVertex+64);dfs_find_strong_component(adjList, adjVertex, depth+1);									}	else // if(visited[adjVertex-1]) 邻接顶点被访问过.{		if(parent[vertex] != adjVertex) // true，则(vertex, adjVertex)就是背向边{								// just for printing effect, 不作为算法的一部分.for(i = 0; i < depth; i++)  printf("           ");	printf("v[%c]->v[%c] (backside)\n", vertex+64, adjVertex+64);// 不作为算法的一部分over.} 			 			 }				temp = temp->next;} 	num[vertex] = ++counter; // 顶点vertex 被访问的序号. // attention, p249: 明确说明 使用dfs 后序遍历设置 顶点编号.
} int min(int a, int b)
{return a>b? b:a;
}

对以上代码的分析） 注意，step1中明确说了后序遍历记录访问序号，参见 第 45 行代码；

测试用例如下：

void main()
{int capacity=VertexNum;	 // 顶点个数AdjList adjList; // 邻接表AdjList adjListReverse; // 反向邻接表BinaryHeap heap; // 大根堆, 用于依次选取 序号最大的边. 堆节点类型是结构体, 因为要存储顶点编号和对应的被访问序号.int row=VertexNum, col=3, i, j;	 							int vertex;int adjArray[VertexNum][VertexNum] = {{2, 4, 0}, // A{3, 6, 0}, // B{1, 4, 5}, // C{5, 0, 0}, // D{0, 0, 0}, // E{3, 0, 0}, // F{6, 8, 0}, // G{6, 10, 0}, // H{8, 0, 0}, // I{9, 0, 0}, // J};// init adjacency list.adjList = init(capacity);	if(adjList==NULL){return;}			printf("\n\n\t === reviww for DFS applie into directed graph ===");printf("\n\t === build adjacency list ===\n");	 for(i=0;i<row;i++){				for(j=0; j<col; j++){if(adjArray[i][j]){insertAdjList(adjList, i, adjArray[i][j], adjArray[i][j]); // 插入节点到邻接表.(无向图权值为全1)}}}printAdjList(adjList);// 使用 dfs 查找强连通分支.// step1: 基于dfs 遍历 有向图G，对顶点的访问顺序编号.printf("\n=== dfs_find_directed_graph(adjList, 2, 1) ===\n");dfs_find_strong_component(adjList, 2, 1);	 // start=1.for(i=1; i<=VertexNum; i++){if(!visited[i]){printf("\n");dfs_find_strong_component(adjList, i, 1);}}// step1 over.printf("\n\t === num array are as follows. ===");printArray(num, VertexNum+1);		//step2: 把G的所有边反向 -> Gr.adjListReverse = init(capacity);	if(adjListReverse==NULL){return;}				printf("\n\t === build reverse adjacency list ===\n");for(i=0;i<row;i++){			for(j=0; j<col; j++){if(adjArray[i][j]){insertAdjList(adjListReverse, adjArray[i][j]-1, i+1, adjArray[i][j]); // 插入节点到邻接表.(无向图权值为全1)}}} // step2 over.printAdjList(adjListReverse);	 // step3: 从序号最大的顶点开始，依次对Gr 进行 dfs.（这里需要建立一个大根堆）	// step3.1: 利用num[] 建立大根堆heap = initBinaryHeap(VertexNum+1); // 因为0号下标不用.for(i=1; i<=VertexNum; i++){insert(createHeapNode(i, num[i]), heap);// 初始化数组为0visited[i] = 0;num[i] = 0;				parent[i] = 0;	} // step3.1 over.printf("\n\t === binary heap is as follows.===");printBinaryHeap(heap);counter=0; // 初始化count=0；// step3.2 依次选取 最大序号的顶点进行dfsprintf("\n=== dfs_find_strong_component(adjListReverse, deleteMin(heap).index, 1) ===\n");while(!isEmpty(heap) && counter!=VertexNum){			vertex = deleteMin(heap).index; // 依次选取 最大访问序号的顶点.		if(!visited[vertex]) // 如果该顶点没有被访问的话.{dfs_find_strong_component(adjListReverse, vertex, 1);}		}	
}

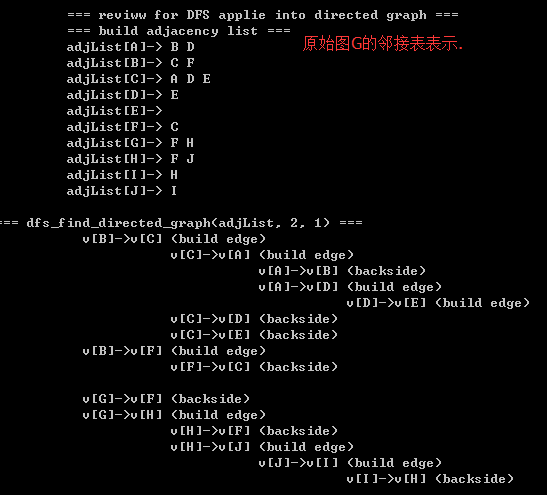
对上面打印结果的分析）如何选取强连通分支呢？（参看深度遍历Gr）

Attention）backside 表示 背向边，而 build edge 表示建立边；显然 背向边的起点和终点属于不同的 强连通分支；而build edge 表示其起点和终点属于同一个强连通分支；

 v[H]->v[G] (backside) // 本次dfs遍历 形成 两个强连通分支 {H} {G}v[H]->v[I] (build edge) // 本次 dfs 遍历 形成 强连通分支 {H, I, J}，结合上一行的结果，则最终的结果是 {H, I, J} {G}v[I]->v[J] (build edge)v[J]->v[H] (backside)v[B]->v[A] (build edge) // 本次遍历dfs 遍历形成 强连通分支 {B, A, C, F}v[A]->v[C] (build edge)v[C]->v[B] (backside)v[C]->v[F] (build edge)v[F]->v[B] (backside)v[F]->v[G] (backside)v[F]->v[H] (backside)v[D]->v[A] (backside) // 本次dfs遍历 形成 {D} {A}，又 A 已经被访问了 所以 只有 {D}v[D]->v[C] (backside) // 本次dfs遍历 形成 {D} {C} 他们都被访问过了，都不作为 新的强分支.v[E]->v[C] (backside) // 本次 dfs 遍形成 {E} {C} 由于 {C} 已经被访问过了，所以形成 {E} 强分支v[E]->v[D] (backside) // 本次 dfs 遍历形成 {E} {D} 由于他们都被访问了，所以 没有强分支

综上所述： 最终的强连通分支有：{G} {B A C F} {D}  {H I J}  {E}