【0】README

1）本文旨在给出 拓扑排序+最短路径算法（有权+无权） 的源码实现 和 分析，内容涉及到 邻接表， 拓扑排序， 循环队列，无权最短路径（广度优先搜索），有权最短路径，二叉堆，迪杰斯特拉算法 等知识；

2）其实，说白了：广度优先搜索算法（计算无权最短路径） 是基于 拓扑排序算法的，而 迪杰斯特拉算法（计算有权最短路径） 是基于 广度优先搜索算法或者说是它的变体算法；上述三者不同点在于： 拓扑排序算法 和 广度优先搜索算法 使用了 循环队列， 而迪杰斯特拉算法使用了 二叉堆优先队列作为其各自的工具；相同点在于：他们都使用了 邻接表来表示图；

3）o. m. g. 差点忘记了，如何计算所有点对最短路径？

3.1）邻接表表示的稀疏图：因为 迪杰斯特拉算法是 计算 单源有权最短路径，故运行顶点个数 次用二叉堆优先队列编写 的 迪杰斯特拉算法即可 计算所有点对最短路径；

3.2）邻接矩阵表示的稠密图：floyd 算法，该算法有三层for 循环 ，内两层循环用于遍历 邻接矩阵的每个元素，最外层循环 用于遍历中转节点，在中转节点的作用下，d[i][j] 之间的路径是否可以减小，伪代码如下：

for(k=1;k<=n;k++)for(i=1;i<=n;i++)for(j=1;j<=n;j++){if(d[i][k]+d[k][j]<d[i][j]){d[i][j]=d[i][k]+d[k][j];path[i][j]=path[i][k];}}

【1】邻接表是图的标准表示方法

https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/review/p216_adjacency_list

0）图的表示方法：稀疏图用邻接表，而稠密图用邻接矩阵，而现实生活中 大多数图都是稀疏的；

1）邻接表的结构体

// 顶点的结构体.
struct Vertex;
typedef struct Vertex* Vertex;
struct Vertex
{// ElementType value; // 要知道顶点是一个标识符，并不是真正的value(而是对value的抽象).int index;Vertex next;
};// 邻接表的结构体
struct AdjList;
typedef struct AdjList* AdjList;
struct AdjList
{int capacity;Vertex* array;
};

2）代码实现如下：

// create vertex with index.
Vertex create(int index)
{Vertex v = (Vertex)malloc(sizeof(struct Vertex));if(v==NULL){Error("failed create() for out of space.");return NULL;}v->index=index;v->next=NULL;return v;
}// 插入 顶点标识符index 到邻接表下标为 start 的位置. 
void insertAdjList(AdjList adjList, int start, int index)
{Vertex temp = adjList->array[start];	while(temp->next){temp = temp->next;}	temp->next = create(index);;	if(temp->next ==NULL){return ;}
}

#include "adjList.h"void main()
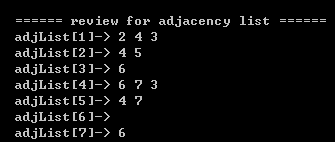
{int capacity=7;	AdjList adjList;int row=7, col=3, i, j;int adjArray[7][3] = {{2, 4, 3},{4, 5, 0},{6, 0, 0},{6, 7, 3},{4, 7, 0},{0, 0, 0},{6, 0, 0}};// init adjacency list.adjList = init(7);	if(adjList==NULL){return;}			printf("\n\n\t ====== review for adjacency list ======\n");			for(i=0;i<row;i++){for(j=0;j<col;j++){if(adjArray[i][j]){insertAdjList(adjList, i, adjArray[i][j]);}}}		printAdjList(adjList);
}

【2】拓扑排序

https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/review/p217_topSort

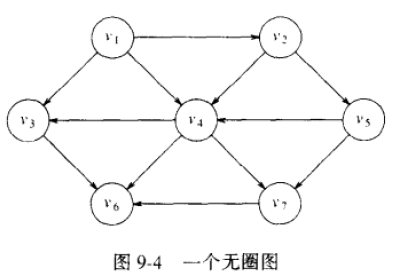
0）定义：拓扑排序是对有向无圈图的顶点的一种排序，它使得如果存在一条从 vi 到 vj 的路径，则在排序中 vj 出现在 vi 的后面；

1）用到的技术： 邻接表， 循环队列， 拓扑排序算法；且使用邻接表的拓扑排序时间复杂度为 O(|E| + |V|)；

2）拓扑排序的steps

step1）把入度为0 的顶点入队列；

step2）当队列不为空时，顶点出队，其邻接顶点的入度减1；

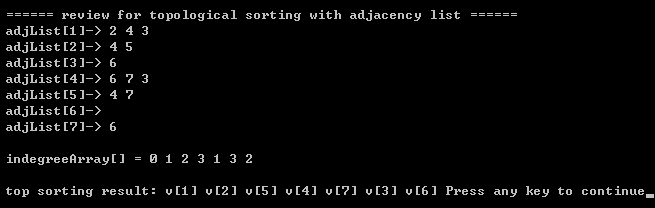
step3）每一个邻接顶点的入度减1 后，若其入度为0 则入队列，转向step2；（别忘记在拓扑排序前，还要统计各个顶点的入度，入度数组indegreeArray 作为输入参数传给 拓扑排序算法）

// 拓扑排序
void topSort(AdjList adjList, Queue queue, int* indegreeArray)
{int i;Vertex* array = adjList->array;Vertex temp;int index;int adjVertex;// step1: 把入度为0的顶点放入队列.for(i=0; i<adjList->capacity; i++) // 切记: 这里入队的value(或i) 从 0 开始取.{if(indegreeArray[i]==0) {enQueue(queue, i);}}//step2: 当队列不为空时，一个顶点v出队，并将与v邻接的所有顶点的入度减1.printf("\n\t top sorting result: ");while(!isEmpty(queue)){index = deQueue(queue); // while 循环已经保证了 队列不可能为空.printf("v[%d] ", index+1); // 注意: 这里的index 要加1，因为元素入队是从 0 开始取的，见上面的入队操作.temp = array[index];while(temp->next){adjVertex = temp->next->index; // 因为 temp->next->index 从1 开始取的,indegreeArray[adjVertex-1]--; // adjVertex 要减1, 而indegreeArray数组从0开始取.if(indegreeArray[adjVertex-1]==0) // step3: 把与顶点v(标识符=index)相邻的，且入度为0的顶点放入队列.{enQueue(queue, adjVertex-1); //入队的value(或index) 从 0 开始取.				}temp = temp->next;}}//  循环结束后: 拓扑排序就是顶点出队的顺序.
}

3）拓扑排序的结果不唯一

4）对于上图的分析（Analysis）

A1）对于上图而言，排序结果可以是 V1， V2， V5， V4， V3， V7， V6  也可以是 V1， V2， V5， V4，V7， V3， V6；

A2）千万不要以为拓扑排序的结果就一定顺着箭头的方向走；

5）排序结果如下：

【3】最短路径算法

【3.1】无权最短路径算法（计算节点间的边数）

https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/review/p220_unweighted_shortest_path

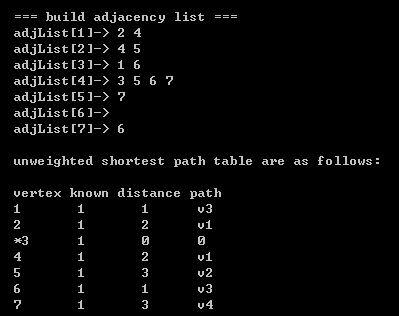
0）算法描述： 给定一个无权图，使用某个顶点s作为 起始顶点，我们想要找出从 s 到 所有其他顶点的最短路径；

1）算法所用技术（techs）：

tech1）邻接表；

tech2）循环队列：为什么无权最短路径算法要用到循环队列？ 因为 要保存遍历到的当前节点的邻接节点，且以 先进先出的顺序输出；

tech3）无权最短路径算法（基于拓扑排序的算法 idea）；

tech4）计算无权最短路径的记录表；

// 记录表的表项
struct Entry;
typedef struct Entry* Entry;
struct Entry
{int known;// 出队后设置为1，表示已处理；int dv; // 起始顶点到当前顶点的距离；int pv; // 引起dv 变化的最后顶点；
};// 记录表的数组
struct UnweightedTable;
typedef struct UnweightedTable* UnweightedTable;
struct UnweightedTable
{	int size;	Entry* array;
};

补充）记录表表项中成员的初始化

//allocate the memory for initializing unweighted table
UnweightedTable initUnweightedTable(int size)
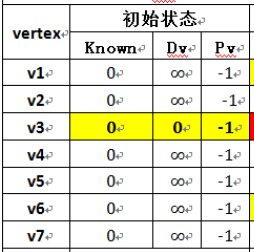
{	int i;UnweightedTable table = (UnweightedTable)malloc(sizeof(struct UnweightedTable));if(table==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}table->size = size;table->array = (Entry*)malloc(size * sizeof(Entry));	if(table->array==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}for(i=0; i<size; i++){table->array[i] = (Entry)malloc(sizeof(struct Entry));if(table->array[i]==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}table->array[i]->known = 0; // known=0 or 1表示 未知 或 已知.table->array[i]->dv= INT_MAX; // dv==distance 等于 INT_MAX 表示不可达. 而 dv=0 表示它自己到自己的path==0.table->array[i]->pv = 0; // pv==path 等于 0 表示不可达，因为pv从1开始取。}return table;
}

2）算法步骤（借用了拓扑排序的算法 idea）：

step1）起始顶点进队，设置其 dv，pv 等于 0；

step2）队列不为空，顶点出队；出队顶点的known设置为1，表明已处理；

step3）遍历出队顶点的每一个邻接顶点，若 邻接顶点的dv 等于 -1 （表不可达），则该邻接顶点进队，设置其 dv，pv；转向step2；

//计算 startVertex顶点 到其他顶点的无权最短路径
void unweighted_shortest_path(AdjList adj, UnweightedTable table, int startVertex, Queue queue)
{		int capacity=adj->capacity;Vertex* arrayVertex = adj->array;Vertex temp;Entry* arrayEntry = table->array;int index; // 顶点标识符(从0开始取)int adjVertex;//step1(初始状态): startVertex 顶点进队.enQueue(queue, startVertex-1); // 切记: 这里入队的value(或i) 从 0 开始取.	arrayEntry[startVertex-1]->dv=0;arrayEntry[startVertex-1]->pv=0;// 初始状态over.// step2: 出队. 并将其出队顶点的邻接顶点进队.while(!isEmpty(queue)){index = deQueue(queue);  // index从0开始取，因为出队value从0开始取，不需要减1.arrayEntry[index]->known=1; // 出队后，将其 known 设置为1.temp = arrayVertex[index];while(temp->next) {adjVertex = temp->next->index; // 邻接节点标识符adjVertex 从1开始取.if(arrayEntry[adjVertex-1]->dv == INT_MAX) // 注意: 下标是adjVertex-1, 且 dv==INT_MAX 表明 index 到 adjVertex 还处于不可达状态，所以adjVertex入队.{enQueue(queue, adjVertex-1); // 入队的value 从 0 开始取，所以减1.arrayEntry[adjVertex-1]->dv = arrayEntry[index]->dv + 1; arrayEntry[adjVertex-1]->pv=index+1; // index 从0开始取，所以index加1.}			temp = temp->next;}		}	
} 

Attention）上述搜索图的算法被称为“广度优先搜索”，因为要遍历出队顶点的每一个邻接顶点，注意是每一个，所以叫做广度；

【3.2】有权最短路径算法（迪杰斯特拉算法）

https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/review/p224_dijkstra_weighted_shortest_path

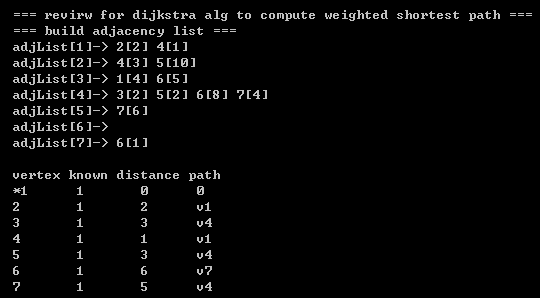
0）算法描述：给定一个有权图，使用某个顶点s作为 起始顶点，我们想要找出从 s 到 所有其他顶点的有权最短路径；

1）算法所用技术（techs）：

tech1）邻接表；

tech2）二叉堆（优先队列）；堆中节点类型为 HeapNode（vertex 和 weight）；为什么迪杰斯特拉算法要用到二叉堆？ 因为 需要保存 当前节点的所有邻接顶点，且 有最小weight 的 邻接顶点先输出，这可以通过小根堆来实现，deleteMin() 就是一个输出的过程；

// 二叉堆的节点类型的结构体.
struct HeapNode;
typedef struct HeapNode* HeapNode;
struct HeapNode
{int vertex;int weight;
};// 二叉堆的结构体.
struct BinaryHeap;
typedef struct BinaryHeap* BinaryHeap;
struct BinaryHeap
{int capacity;int size;HeapNode array;
};

tech3）迪杰斯特拉算法；

tech4）计算有权最短路径的记录表（同无权的记录表）；

// 邻接表的表项结构体.
struct Entry;
typedef struct Entry* Entry;
struct Entry
{int known;int dv;int pv;
};// 有权路径记录表的结构体.
struct WeightedTable;
typedef struct WeightedTable* WeightedTable;struct WeightedTable
{	int size;	Entry* array;
};

//allocate the memory for initializing unweighted table（计算有权路径的记录表项的初始化）
WeightedTable initWeightedTable(int size)
{	int i;WeightedTable table = (WeightedTable)malloc(sizeof(struct WeightedTable));if(table==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}table->size = size;table->array = (Entry*)malloc(size * sizeof(Entry));	if(table->array==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}for(i=0; i<size; i++){table->array[i] = (Entry)malloc(sizeof(struct Entry));if(table->array[i]==NULL){Error("failed initUnweightedTable() for out of space.");return NULL;}table->array[i]->known = 0; // known 等于 0 or 1 表示 未知 or 已知.table->array[i]->dv= INT_MAX; // dv==distance 等于 INT_MAX 表示不可达.(有权路径表示weight)table->array[i]->pv = 0; // pv==path 等于 0 也表示不可达.}return table;
} 

2）算法步骤

step1）从未知（known==0）顶点中选取 dv 最小的顶点作为初始顶点；初始顶点对应的HeapNode节点类型插入堆（insert操作）；

step2）堆不为空，执行deleteMin()操作；设置被删除顶点为已知（其known=1）；遍历被删除顶点的每一个邻接顶点；

step2.1）如其未知（known==0）

step2.1.1）且若更新后的权值（路径长）比更新前的权值（路径长）小的话

step2.1.1.1）构建该节点的HeapNode节点类型并插入堆且更新路径长；

补充）迪杰斯特拉算法的结束标志是：当 所有顶点的状态都是已知（known==1）的时候，算法结束；

//计算 startVertex顶点 到其他顶点的无权最短路径
// adj:邻接表（图的标准表示方法）, table: 计算有权最短路径的配置表，heap：用于选取最小权值的邻接顶点的小根堆.
void dijkstra(AdjList adj, WeightedTable table, int startVertex, BinaryHeap heap)
{		int capacity=adj->capacity;Vertex* arrayVertex = adj->array;Vertex temp;Entry* arrayEntry = table->array;int index; // 顶点标识符(从0开始取)int adjVertex;struct HeapNode node;int weight;int i=0; // 记录已知顶点个数（ known == 1 的 个数）.//step1(初始状态): startVertex 顶点插入堆. startVertex 从1 开始取.node.vertex=startVertex-1; // 插入堆的 node.vertex 从 0 开始取，所以startVertex-1.node.weight=0;insert(heap, node); // 插入堆.arrayEntry[startVertex-1]->dv=0;arrayEntry[startVertex-1]->pv=0;// 初始状态over.// step2: 堆不为空，执行 deleteMin操作. 并将被删除顶点的邻接顶点插入堆.while(!isEmpty(heap)){		if(i == capacity) // 当所有 顶点都 设置为 已知（known）时，退出循环.{break;}index = deleteMin(heap).vertex;  // index表示邻接表下标，从0开始取，参见插入堆的操作.arrayEntry[index]->known=1; // 从堆取出后，将其 known 设置为1.i++; // 记录已知顶点个数（ known == 1 的 个数）.temp = arrayVertex[index];		while(temp->next) {adjVertex = temp->next->index; // 邻接节点标识符adjVertex 从1开始取.weight = temp->next->weight; // 取出该邻接顶点的权值.if(arrayEntry[adjVertex-1]->known == 0) // 注意: 下标是adjVertex-1, 且known==0 表明 adjVertex顶点还处于未知状态,所以adjVertex插入堆.{if(arrayEntry[adjVertex-1]->dv > arrayEntry[index]->dv + weight ) // [key code] 当当前权值和 比 之前权值和 小的时候 才更新，否则不更新.{node.vertex=adjVertex-1; // 插入堆的 node.vertex 从 0 开始取.node.weight=weight;insert(heap, node); // 插入堆.arrayEntry[adjVertex-1]->dv = arrayEntry[index]->dv + weight; // [also key code]arrayEntry[adjVertex-1]->pv=index+1; // index 从0开始取，所以index加1.	}}			temp = temp->next;}printWeightedtable(table, 1); // 取消这行注释可以 follow 迪杰斯特拉 alg 的运行过程.}	
} 

【补充】以HeapNode 为数据类型的二叉堆优先队列

0）为什么我要提及这个二叉堆？因为 这个二叉堆 和他家的不一样，其数据类型不是 单纯的 int， 而是一个结构体类型，我们只需要在 二叉堆中 将 HeapNode 类型定义为 ElementType 即可。

1）intro： 迪杰斯特拉法用到了 二叉堆优先队列，而二叉堆优先队列 的 数组（节点）类型是 HeapNode；

2）结构体介绍

// 二叉堆的节点类型的结构体.
struct HeapNode;
typedef struct HeapNode* HeapNode;
struct HeapNode
{int vertex;int weight;
};// 二叉堆的结构体.
struct BinaryHeap;
typedef struct BinaryHeap* BinaryHeap;
struct BinaryHeap
{int capacity;int size;HeapNode array;
};

3）二叉堆优先队列的 操作（重点关注其 基于上滤的插入操作 和 基于下滤的deleteMin操作）

// judge whether the heap is empty or not.
int isEmpty(BinaryHeap heap)
{return heap->size == 0;
}// build binary heap with capacity.
BinaryHeap buildHeap(int capacity)
{BinaryHeap heap = (BinaryHeap)malloc(sizeof(struct BinaryHeap));if(!heap){Error("failed buildHeap() for out of space.");return NULL;}heap->capacity = capacity;heap->size = 0; // startup of the heap is 1. so ++size when insert.// allocate memory for heap->array.heap->array = (ElementType*)malloc(sizeof(ElementType) * capacity);if(!heap->array){Error("failed buildHeap() for out of space.");return NULL;}heap->array[0].weight = INT_MIN; // heap->array starts from 1 not 0, so let heap->array[0] = INT_MIN.return heap;
}// 插入操作 based on 上滤操作.
void insert(BinaryHeap heap, ElementType data)
{if(heap->size == heap->capacity-1){Error("failed insert() for heap is full.");}	percolateUp(heap, data);
}// 上滤操作(key operation)
void percolateUp(BinaryHeap heap, ElementType data)
{int i;// 必须将size++.for(i=++heap->size; data.weight < heap->array[i/2].weight; i/=2){heap->array[i] = heap->array[i/2];}heap->array[i] = data;
}// delete minimal from heap based on percolateDown().
ElementType deleteMin(BinaryHeap heap)
{		ElementType temp;if(heap->size==0){Error("failed deleteMin() for the heap is empty");return temp;}	swap(&heap->array[1], &heap->array[heap->size--]); // 将二叉堆的根和二叉堆的最后一个元素交换，size--。percolateDown(heap, 1); // 执行下滤操作.return heap->array[heap->size+1];
}// 下滤操作(key operation)
void percolateDown(BinaryHeap heap, int i)
{int child;ElementType temp;	for(temp=heap->array[i]; (child=leftChild(i))<=heap->size; i=child){				if(child<heap->size && heap->array[child].weight > heap->array[child+1].weight){child++;}if(temp.weight > heap->array[child].weight) // 比较是和 temp=heap->array[index] 进行比较.{			heap->array[i] = heap->array[child];}else{					break;}}heap->array[i] = temp;	
}int leftChild(int index)
{return 2*index;
}// swap a and b.
void swap(ElementType* a, ElementType* b)
{ElementType t;t = *a;*a = *b;*b = t;
}void printBinaryHeap(ElementType *array, int size)
{int i;for(i=1; i<=size; i++){printf("\n\t heap->array[%d] = ", i);		printf("%d", array[i].weight);		}printf("\n");
}