MLA原理讲解

多头潜在注意力机制

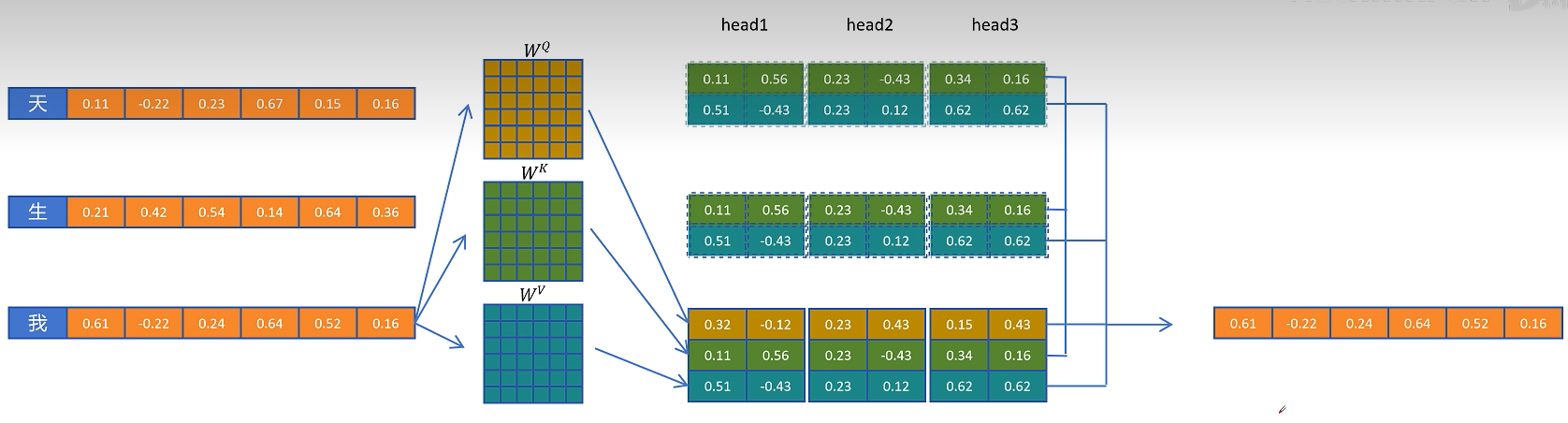
首先我们来回忆一下大模型生成时一个标准多头注意力机制，首先对于第一个token，它的特征向量为H，通过Query权重矩阵，Key权重矩阵和Value权重矩阵，分别得到这个token的Q向量、K向量和V向量。然后经过\(\text{softmax}\left( \frac{Q \cdot K}{\sqrt{d}} \right) \cdot V\)计算得到输出向量O。这个输出向量O将进入这个block的DeepSeekMoE层，最终通过多个transformer块得到最终这个token的特征向量。接一个分类头可以预测得到下一个token。

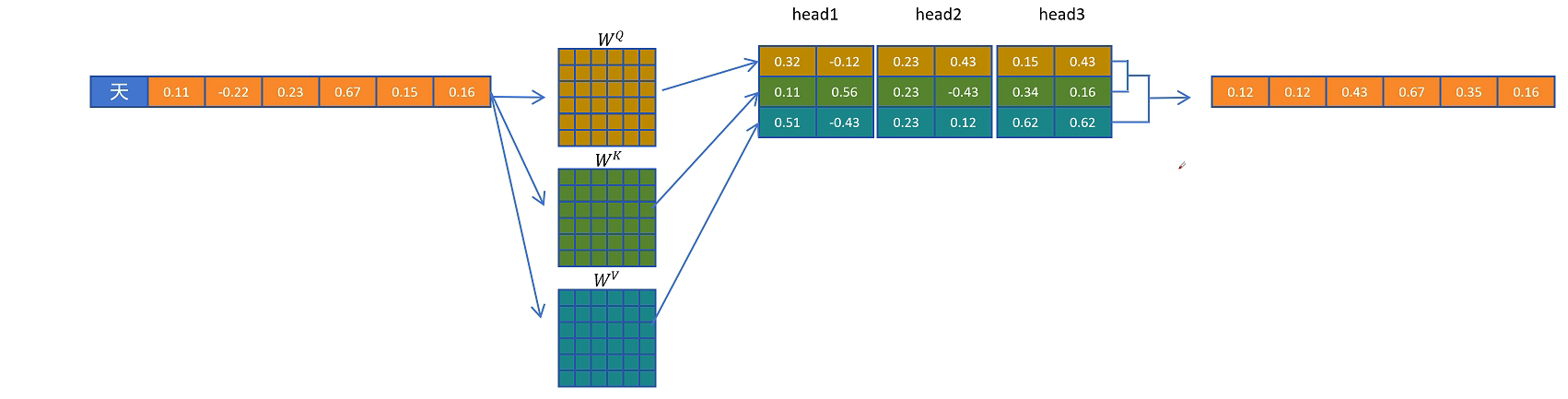
将新生成的token拼接到输入序列，用这两个token的特征向量经过Query权重矩阵，Key权重矩阵，Value权重矩阵，然后分别得到两个token的Q向量、K向量和V向量。第一个token只能跟自己进行注意力计算，输出这一层这个token的输出向量O（重复计算），以便传入下一层进行计算。第二个token可以看到第一个token和自己，第二个token的Q向量，分别和第一个token和自身的K向量计算点积得到权重，用权重乘以两个token的V向量，得到第二个token在这一层的输出向量，最终计算出第三个token。在计算第二个token时，第一个token的输出向量属于重复计算。

 

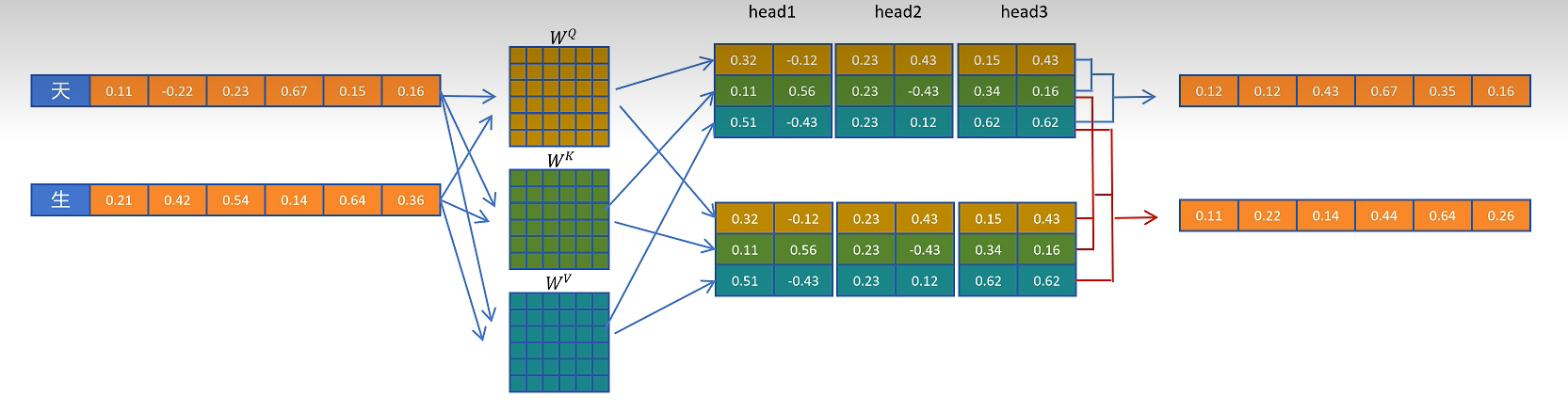
 那是否可以缓存第一个token计算的中间变量，并且也只保留生成新token时所需要的中间变量？我们可以发现在计算第二个token时，只用到了第一个token的K和V向量，所有我们只需要缓存第一个token的K和V向量，这个缓存就叫做KV cache。

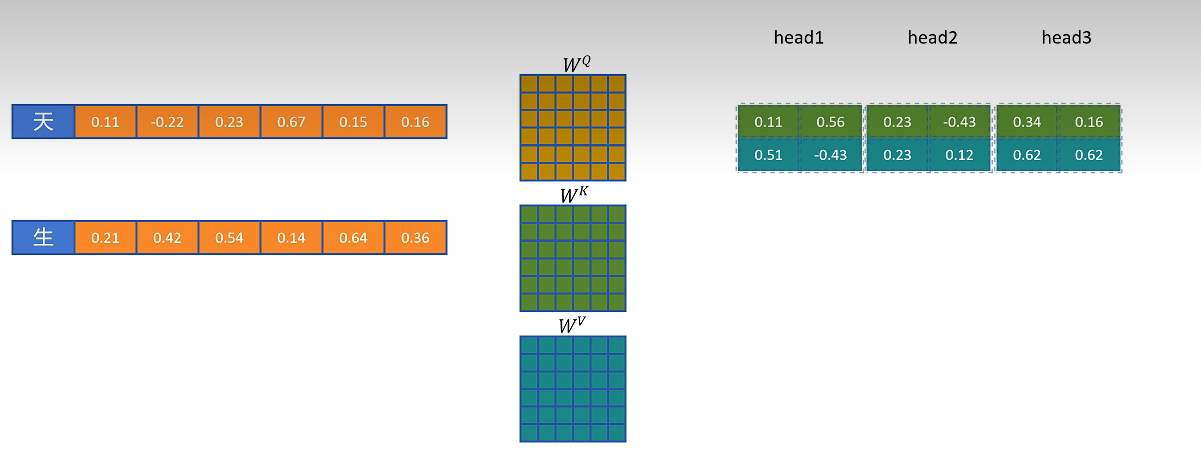
 有了KV Cache之后，我们再来看一下生成的第三个token的过程，这时第一个token就不需要重新计算了，只计算第二个token的Q，K，V向量。然后从KV Cache中取出第一个token的K和V向量进行第二个token的特征向量计算，计算的同时第二个token的K和V向量也存入了KV  Cache。最终计算得出第三个token。

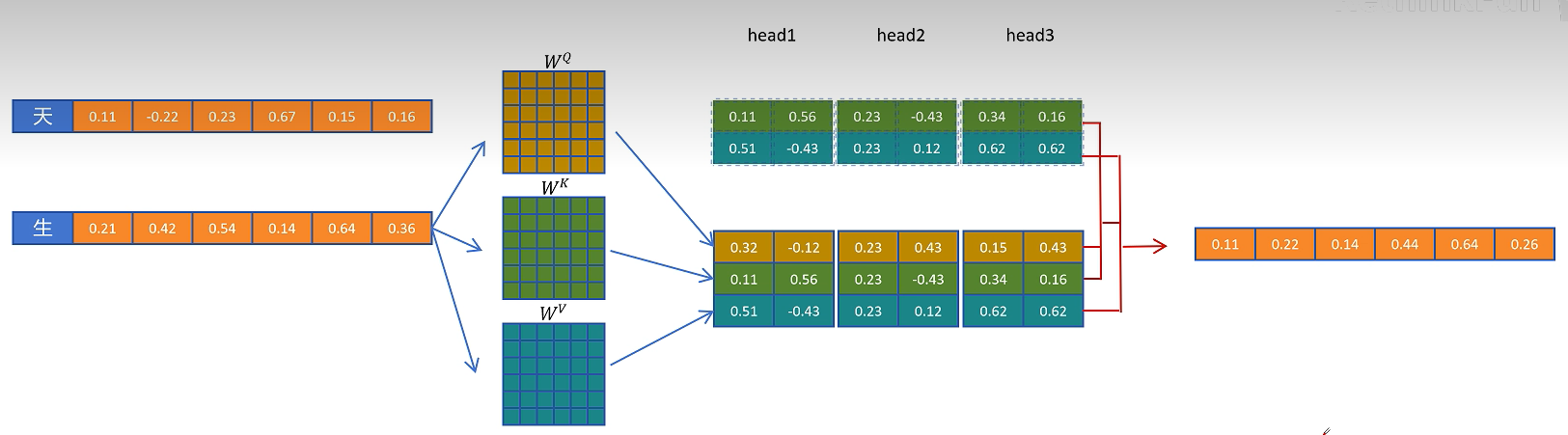
 接着进入计算第四个token的过程，此时计算第三个token在每一层的KV向量，并结合KV Cache里缓存的其他token的K和V向量，更新第三个token的特征向量。

 看起来不错。KV Cache减少了推理时的计算量，加快了推理速度。但是它是以宝贵的显存空间来换取计算量的减少，并且随着生成序列越来越长，KV Cache会越来越大

对此人们也想了很多办法，相比标准的transformer架构里的多头注意力MHA，人们提出了组查询注意力GQA和多查询注意力MQA。

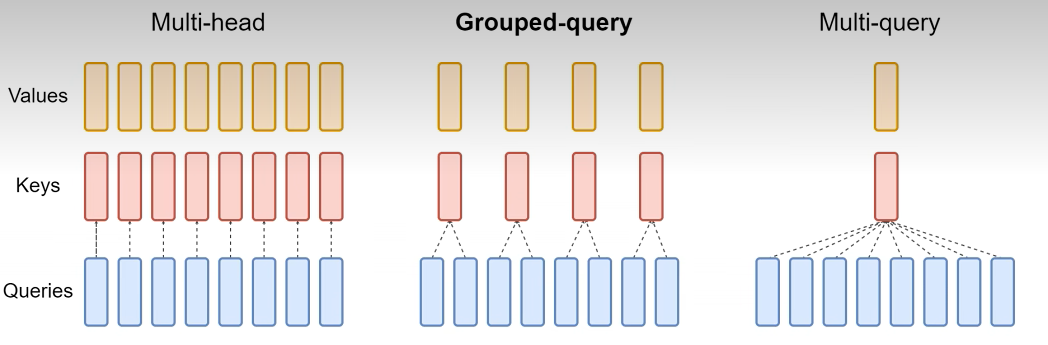
 比如MQA生成3个头的Q向量但是只生成一个头的K和V向量，然后复制和共享KV向量，与Q向量一起来进行注意力计算，这样就大大减少了KV Cache的大小，但是这样会大大影响模型的性能。

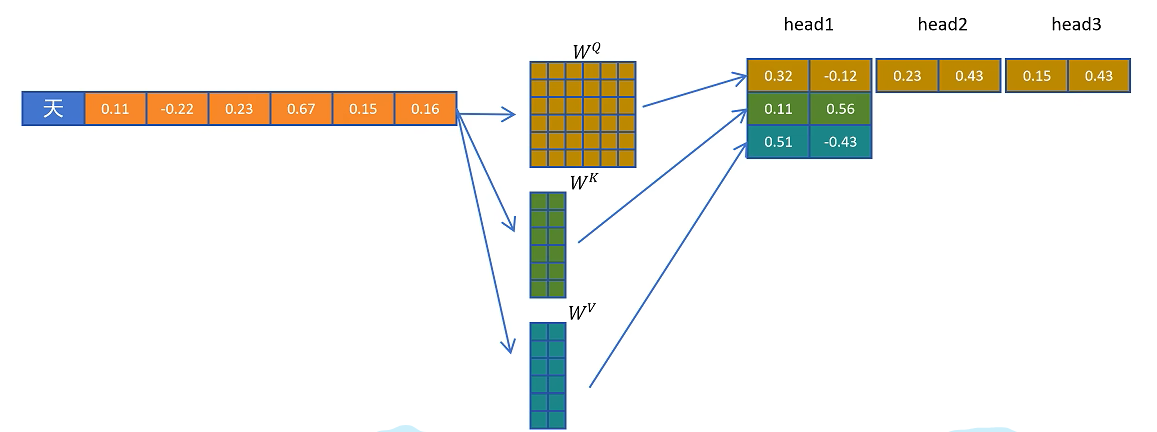
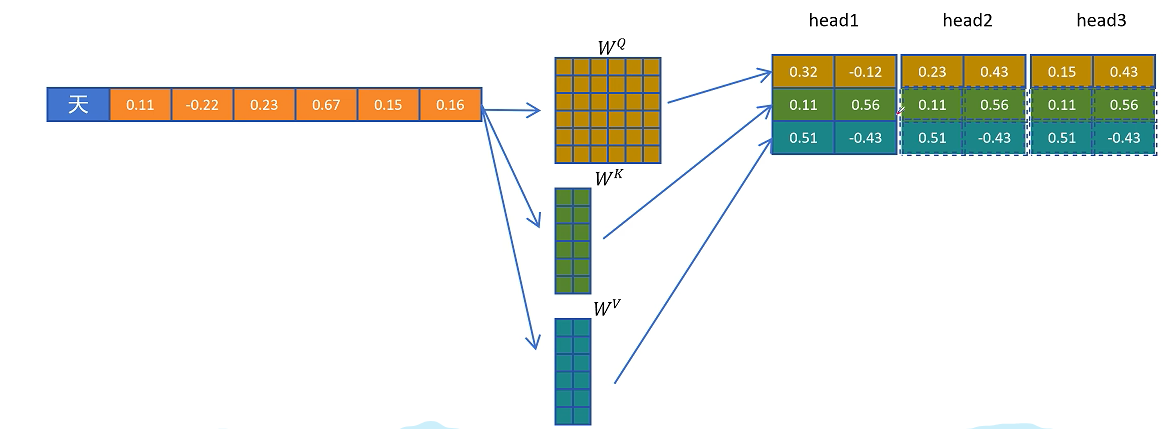
 为了折中，人们提出了分组注意力机制GQA，每组Query共享一个K和V向量，因为MQA和GQA相比标准多头注意力MHA的参数量会减少，为了实验的公平，通过增加更多的层。让同等参数量的MQA、GQA和MHA进行比较。

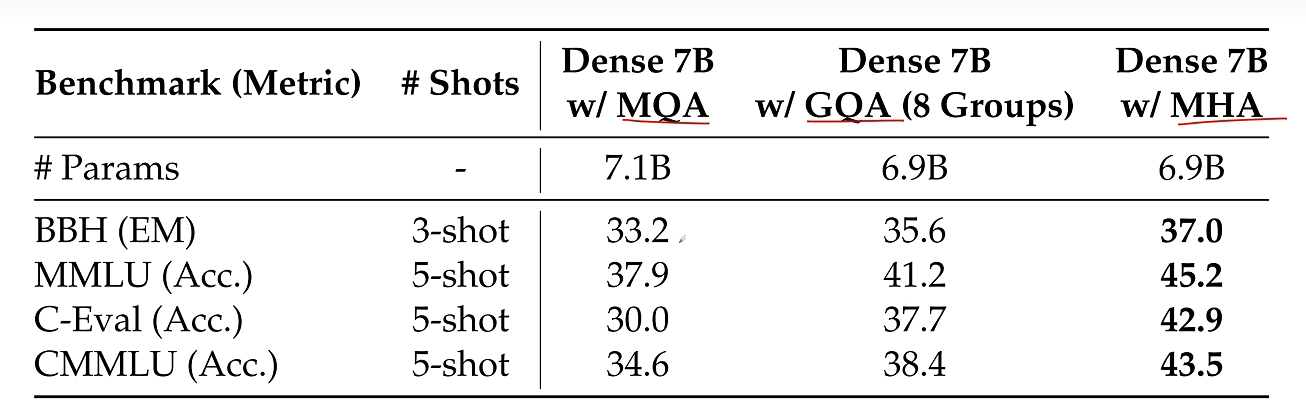
 有没有既能减少KV Cache又不影响模型性能，甚至可以提高模型性能的做法呢？这种方法被DeepSeek找到了，那就是多头潜在注意力机制MLA。

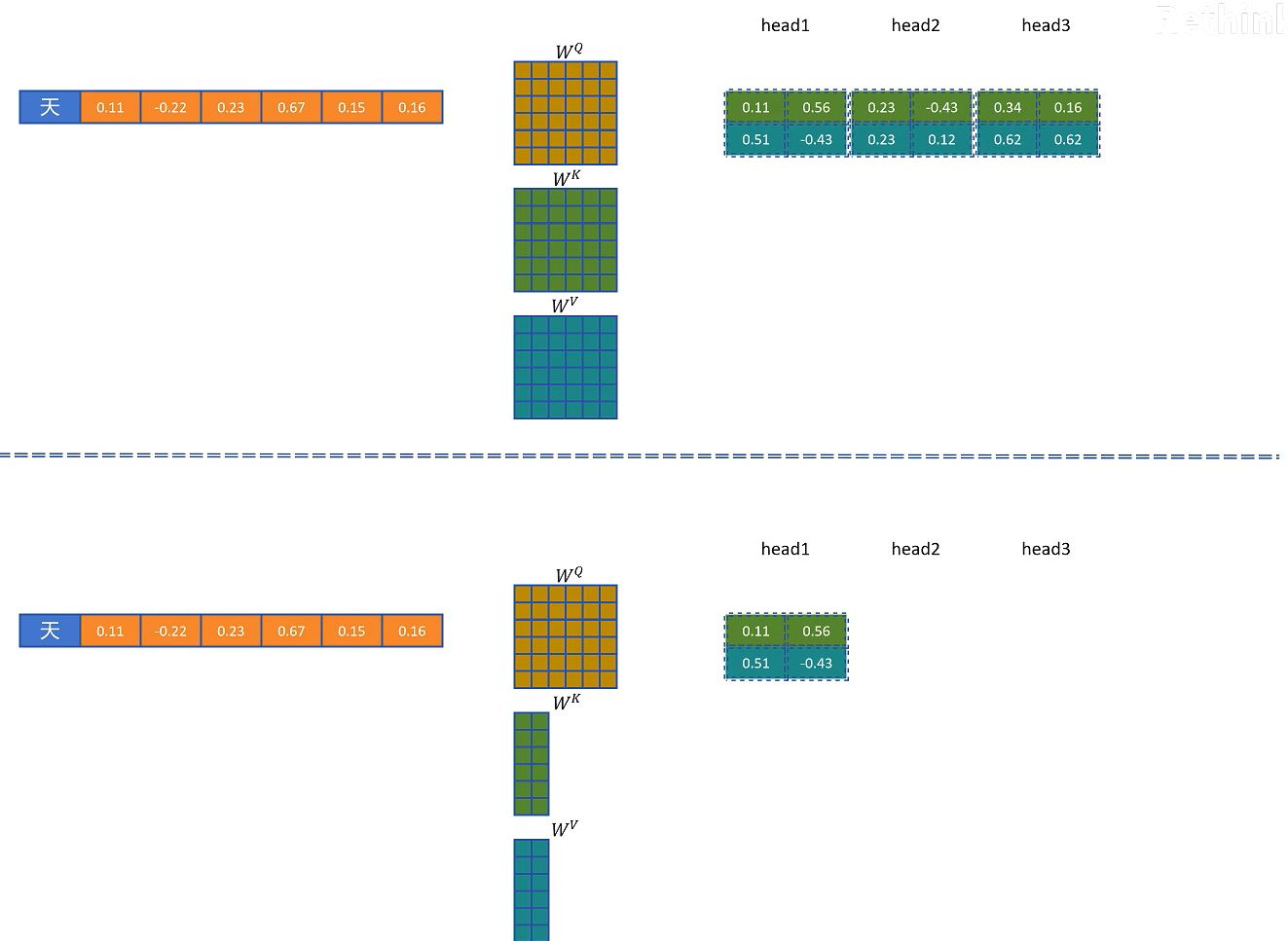
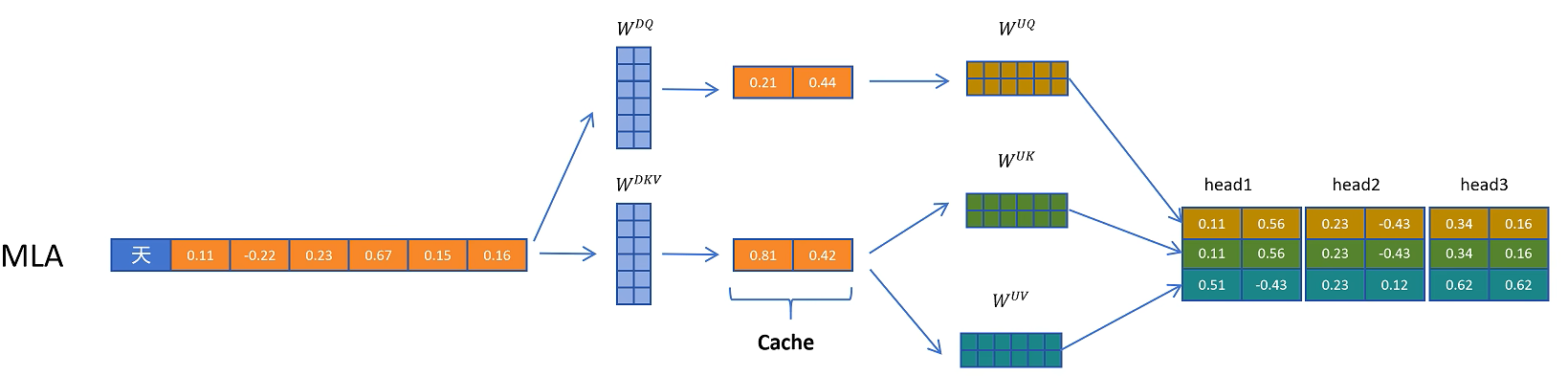
 它的原理也很简单，就是对token的特征向量，通过一个参数矩阵进行压缩转换，这个参数我们把它叫做W_dkv，d就是down的意思，表示向下压缩，kv就是K和V向量的意思。比如这里原来的特征维度是6，经过W_dkv压缩到了2维，然后我们只需要缓存这个2维的KV向量，在进行计算时需要用到真实的K和V向量，再从KV压缩向量，通过2个解压矩阵转换为原来的维度就可以了。

把KV压缩向量进行解压，投影到实际K向量的参数矩阵叫做W_uk,u是up的意思，表示向上升维，k表示K向量。同理对V向量进行解压的升维的参数矩阵叫做W_uv.

这时我们可以比较一下原始MHA的KV Cache的缓存量以及MQA的缓存量

 

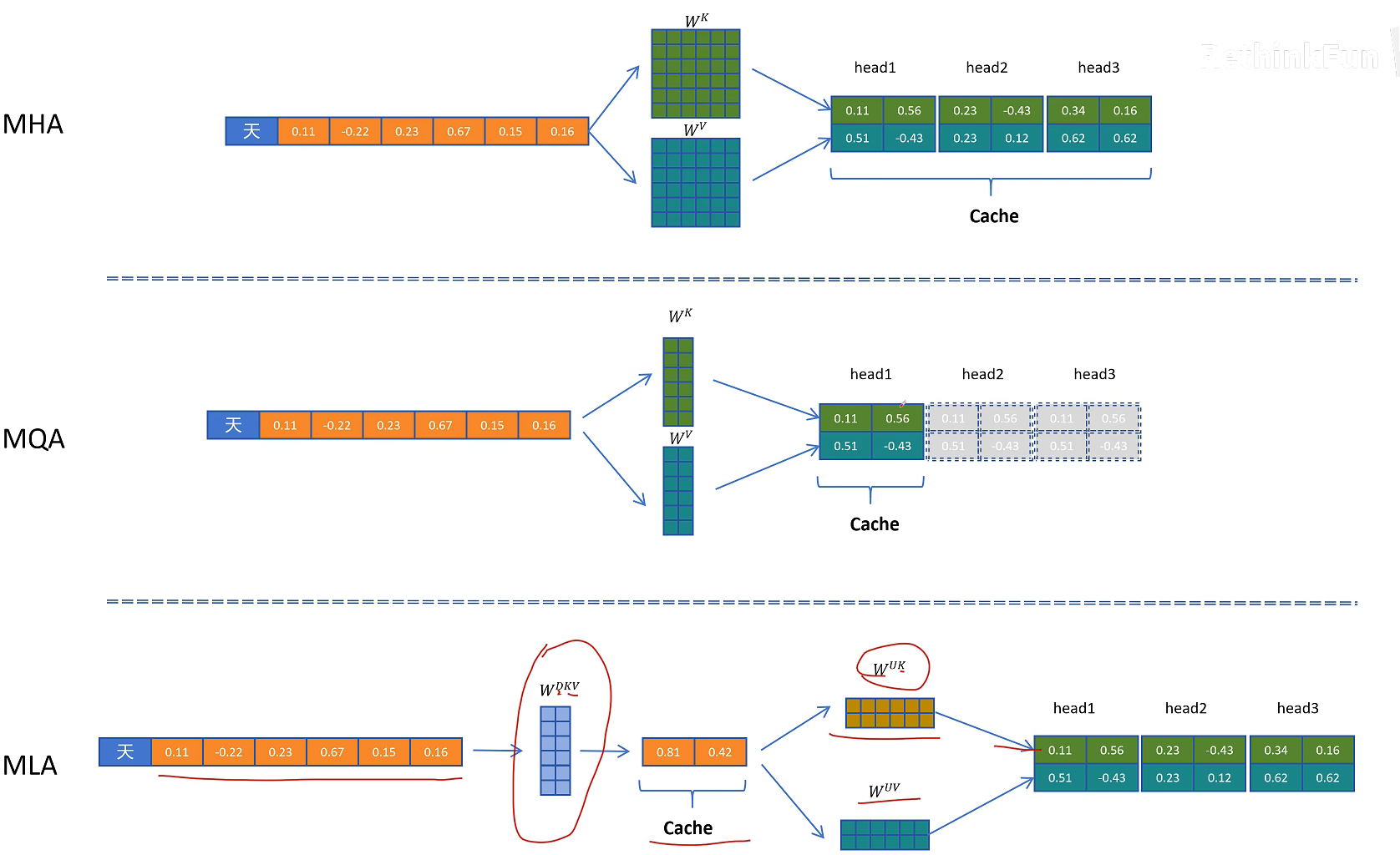
 MLA确实能减少KV Cacha的缓存量，但是会影响模型的效果吗？DeepSeek同样进行了实验来验证。结果惊喜的发现，MLA的模型效果比MHA还要好。所以MLA相比标准的MHA不仅KV Cacha大幅减小，而且意想不到的是模型效果还有提升。

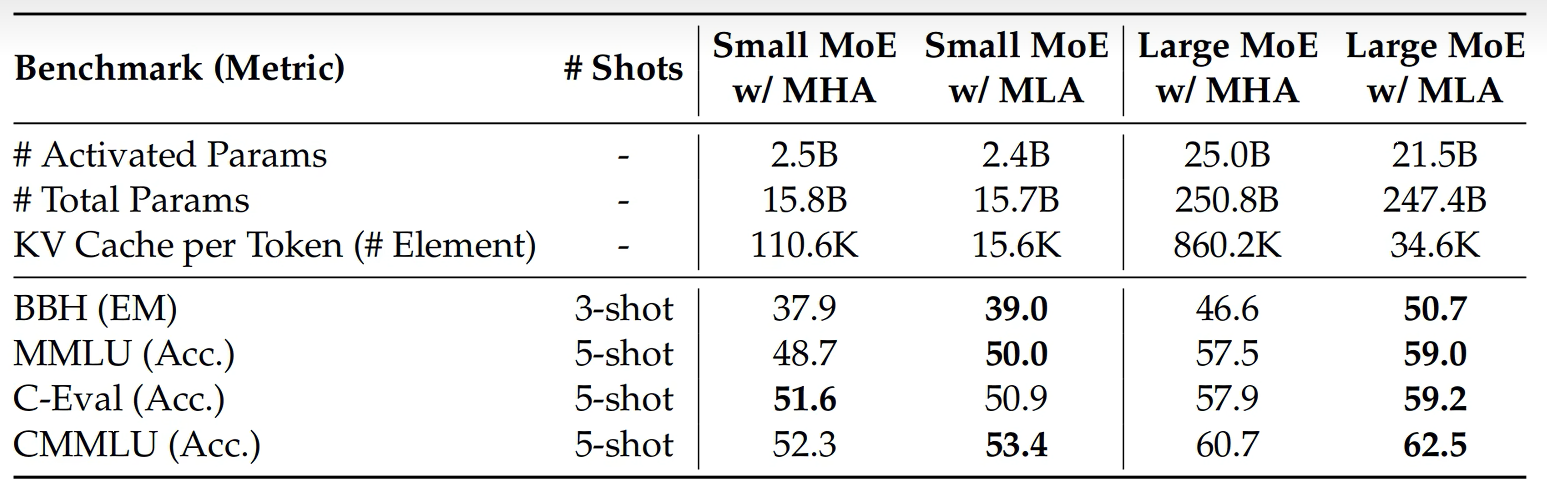
 这一切都非常不错，但是KV Cache的本意是什么呢？它是为了减少推理时对之前token的KV向量的计算而产生的，MLA因为缓存了压缩的KV Cache而减小了显存占用，但是在取出缓存后K和V不能直接使用，还是要经过解压计算才可以，这不是在推理时又引入了解压这个额外的计算吗？这和KV Cache的初衷是相悖的。

我们看一下KV Cache的推理过程，标准的MHA对于当前的token计算QKV，然后缓存K和V向量，对于之前的token，直接从缓存中取出K和V向量就可以，然后进行Attention的计算。

但是MLA对于当前token的计算，Q的计算不变，但是在K和V的计算时，先通过W_dkv参数矩阵进行压缩，然后生成压缩的KV的隐特征C_kv,并将C_kv缓存在KV Cache里。KV向量通过将KV的压缩隐特征C_kv分别与解压参数矩阵W_uk和W_uv进行相乘，得到当前token的K和V向量。对于之前的token，则从KV Cache里取出压缩的隐特征向量C_kv，然后经过K和V向量的解压参数矩阵投影，得到可以计算的K和V向量。

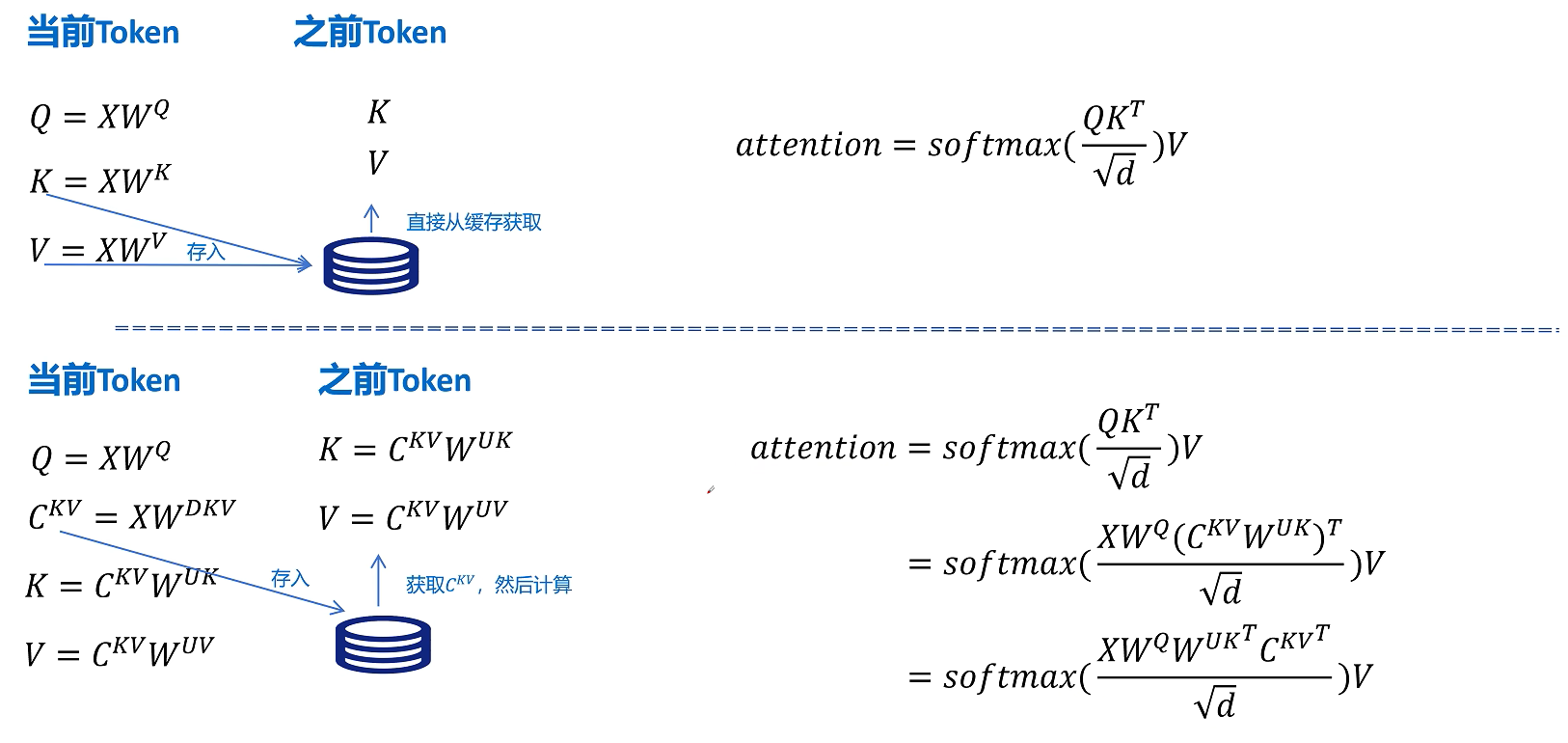
 所以进行注意力计算时它的公式是这样的，我们主要关注的是这里的Q和K_T,代入Q=X*W_q, K=C_kv * W_uk,其中W_q * W_uk可以进行融合，这个融合可以在推理之前计算好，这样在推理时就不用额外对K的解压计算了，这样我们通过矩阵相乘的结合律对矩阵进行提前的融合，就可以规避MLA引入推理时因解压隐特征带来的额外计算了

 刚才我们详细看了W_uk可以和W_q进行融合，同样对于V向量进行解压的W_uv也可以和W_o进行融合。

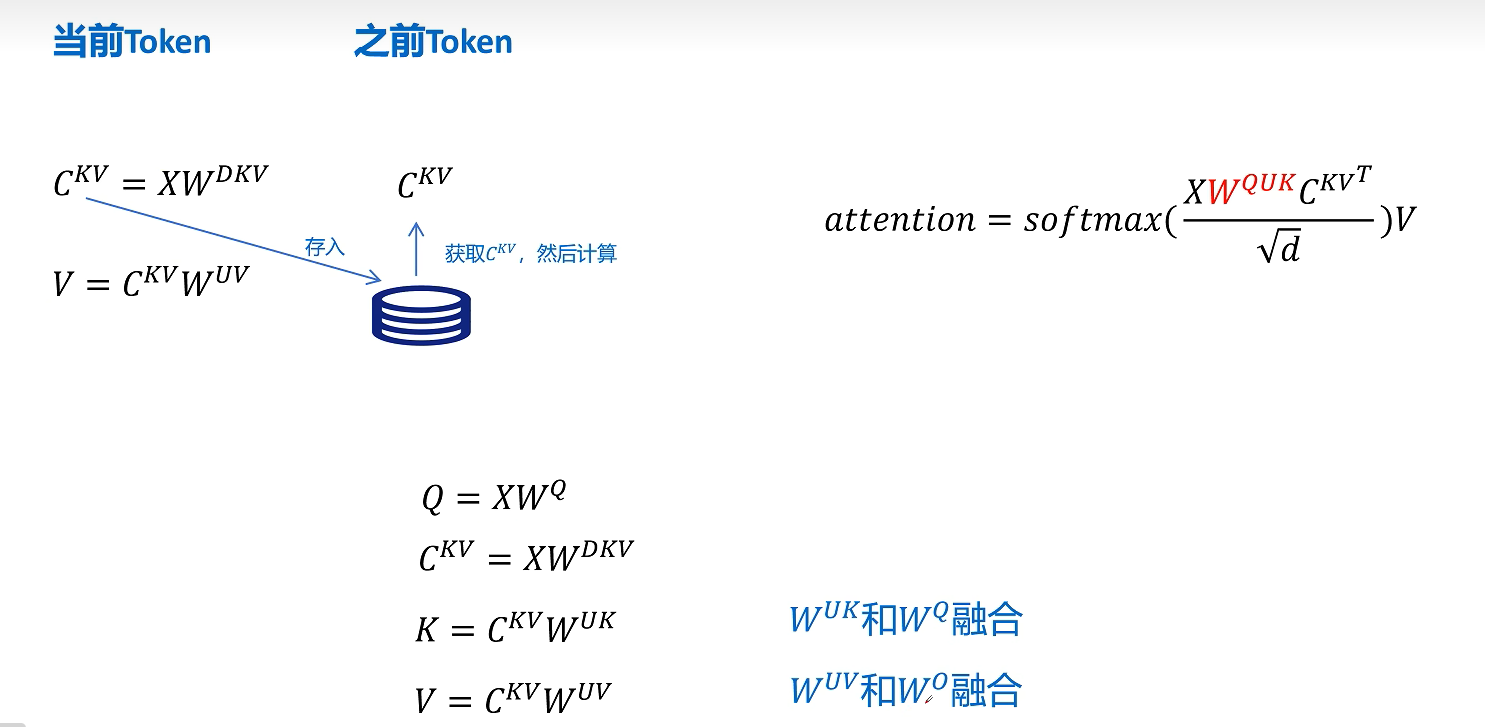
 MLA除了对K和V向量进行压缩外，对Q向量也进行了压缩，这样的好处是降低了参数量，而且可以提高模型的性能，可以看到这里通过W_dq对Q向量进行了压缩，通过W_uq对Q向量进行解压，但是Q的隐向量不需要缓存，只需要缓存KV公用的KV压缩隐向量即可。

 刚才我们一直没有讨论为止编码，确切的说是旋转位置编码RoPE，现在旋转位置编码RoPE已经是大模型默认的位置编码方式了，我们知道旋转位置编码需要对每一层的Q和K向量进行旋转。而且根据token位置的不同，旋转矩阵的参数也不同，这里以第i个token的Q向量和第j个token的K向量进行点积运算为例。如果不考虑旋转位置编码，就是之前所说的W_uk可以和W_q进行融合。但是如果考虑旋转矩阵呢？因为不同位置的旋转矩阵不同，这里我们用R_i和R_j表示，可以发现如果增加了旋转矩阵，它就出现在了W_q和W_uk之间，而且因为R_i和R_j和位置相关，它不能和这两个矩阵进行融合，所以它破坏了之前想到的推理时矩阵提前融合的方案。

 DeepSeek最终想到了一个解决方案，就是给Q和K向量额外增加一些维度来表示位置信息。对于Q向量，它通过W_qr为每一个头生成一些原始特征，这里q代表Q向量，r代表旋转位置编码。

 然后通过旋转位置编码增加位置信息。

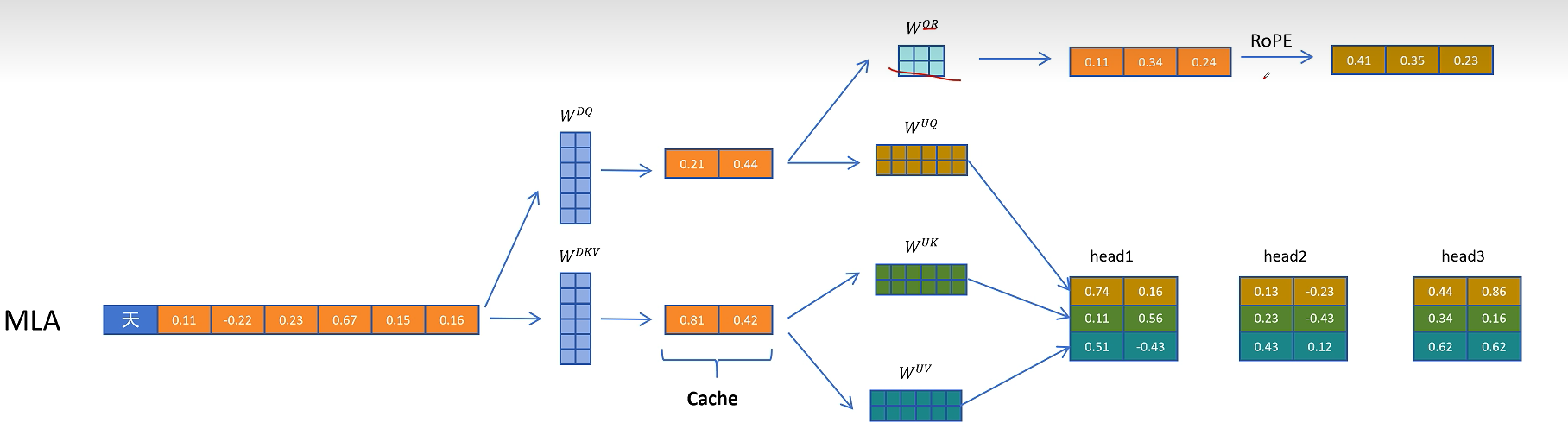
 再把生成带有位置信息的特征拼接到每个注意力头的Q向量。

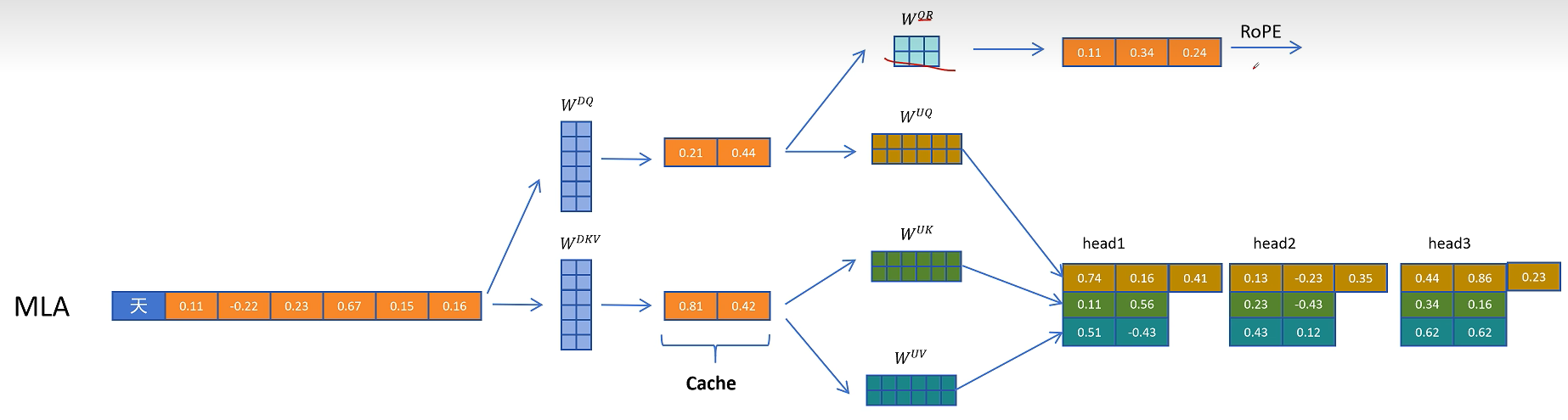
 对于K向量，通过W_kr矩阵生成一个头的共享特征，通过旋转位置编码增加位置信息。

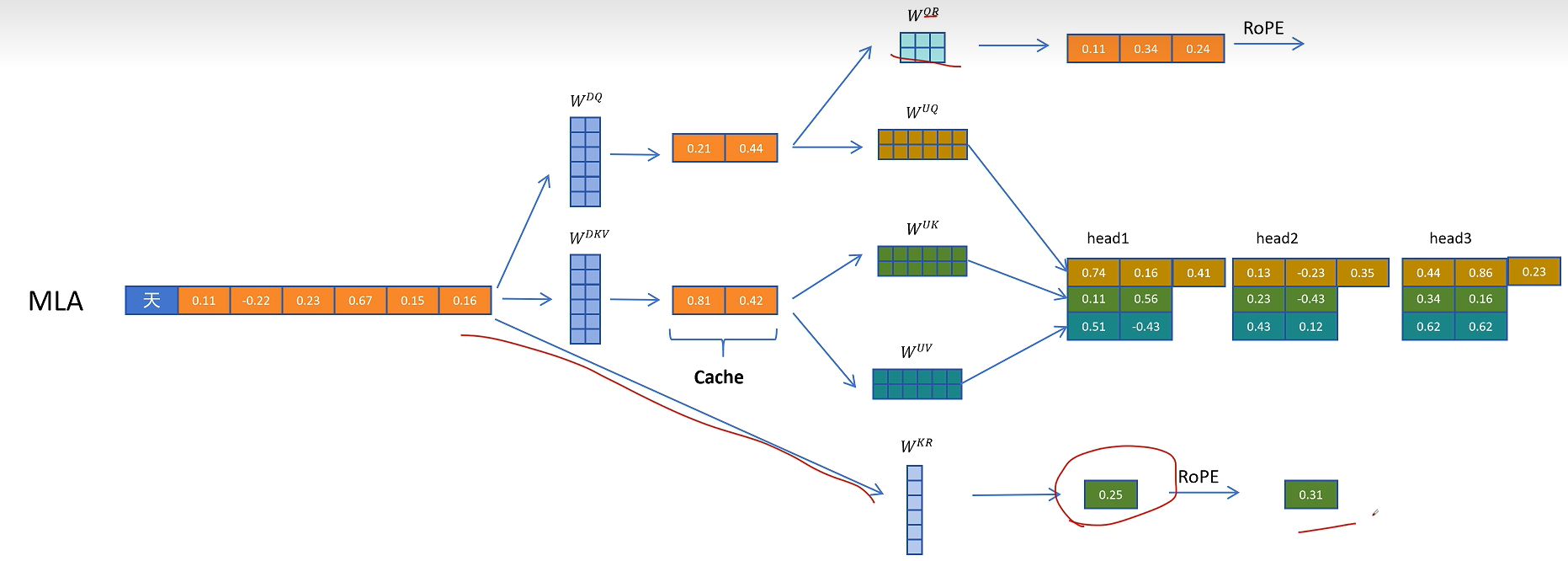
 然后复制到多个头共享位置信息。

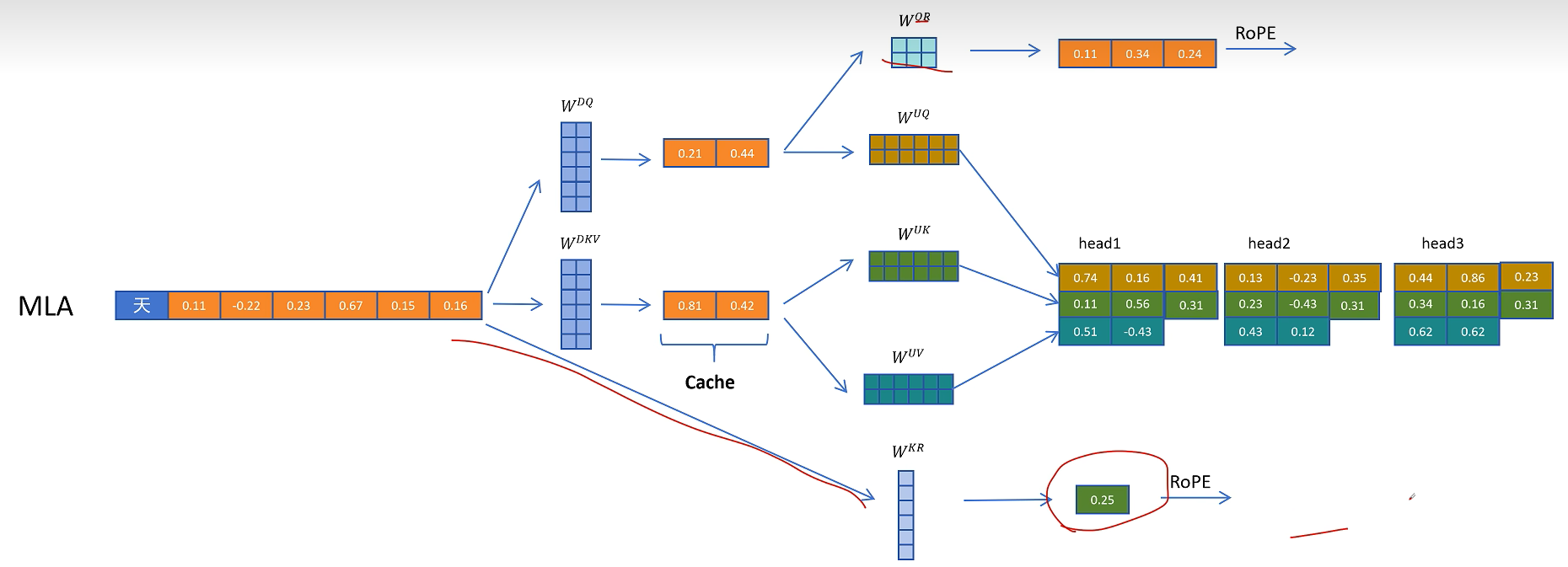
 这里多头共享带位置编码的K向量也需要被缓存，以便在生成带位置信息的K向量时用到。

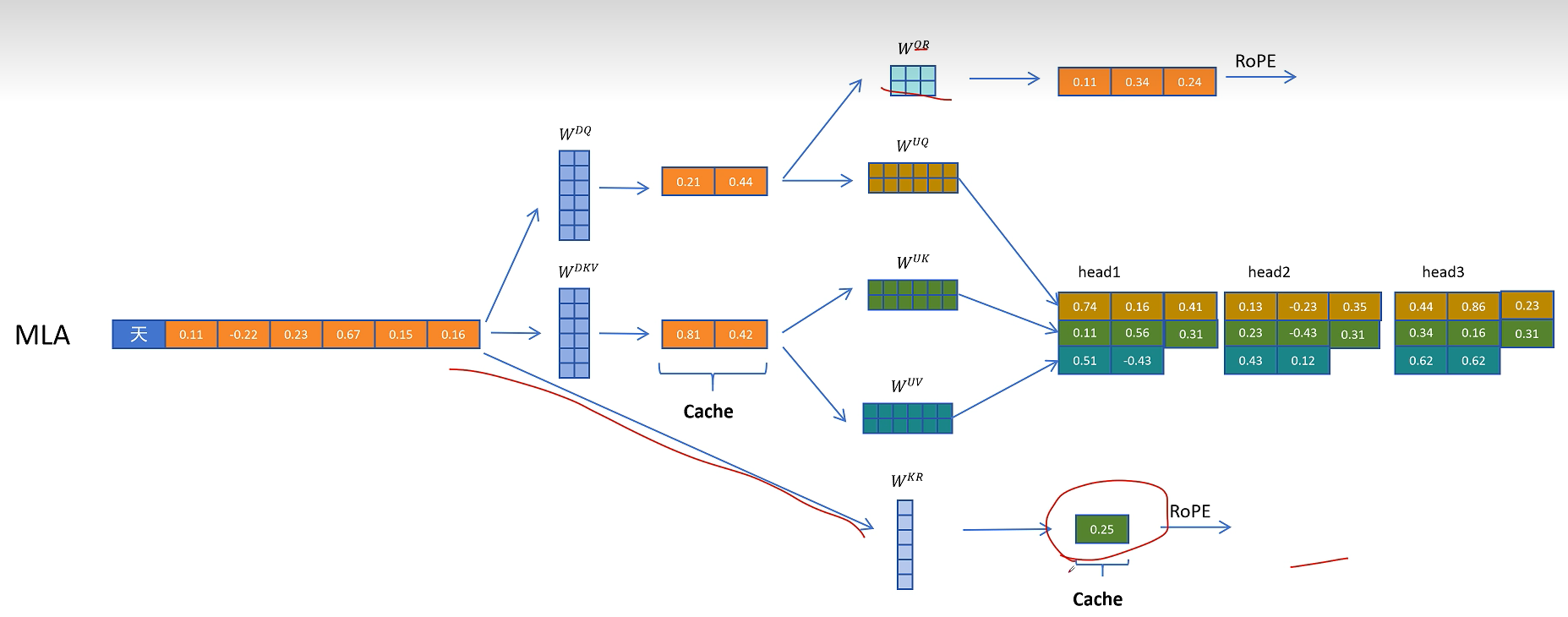
 在推理时不带旋转位置编码的Q和K进行点积运算，这里的计算可以用融合的矩阵来消除解压操作。带旋转位置编码的部分进行点积计算，然后得到的两个值相加，就相当于对拼接了位置信息的完整的Q和K向量进行点积操作的值。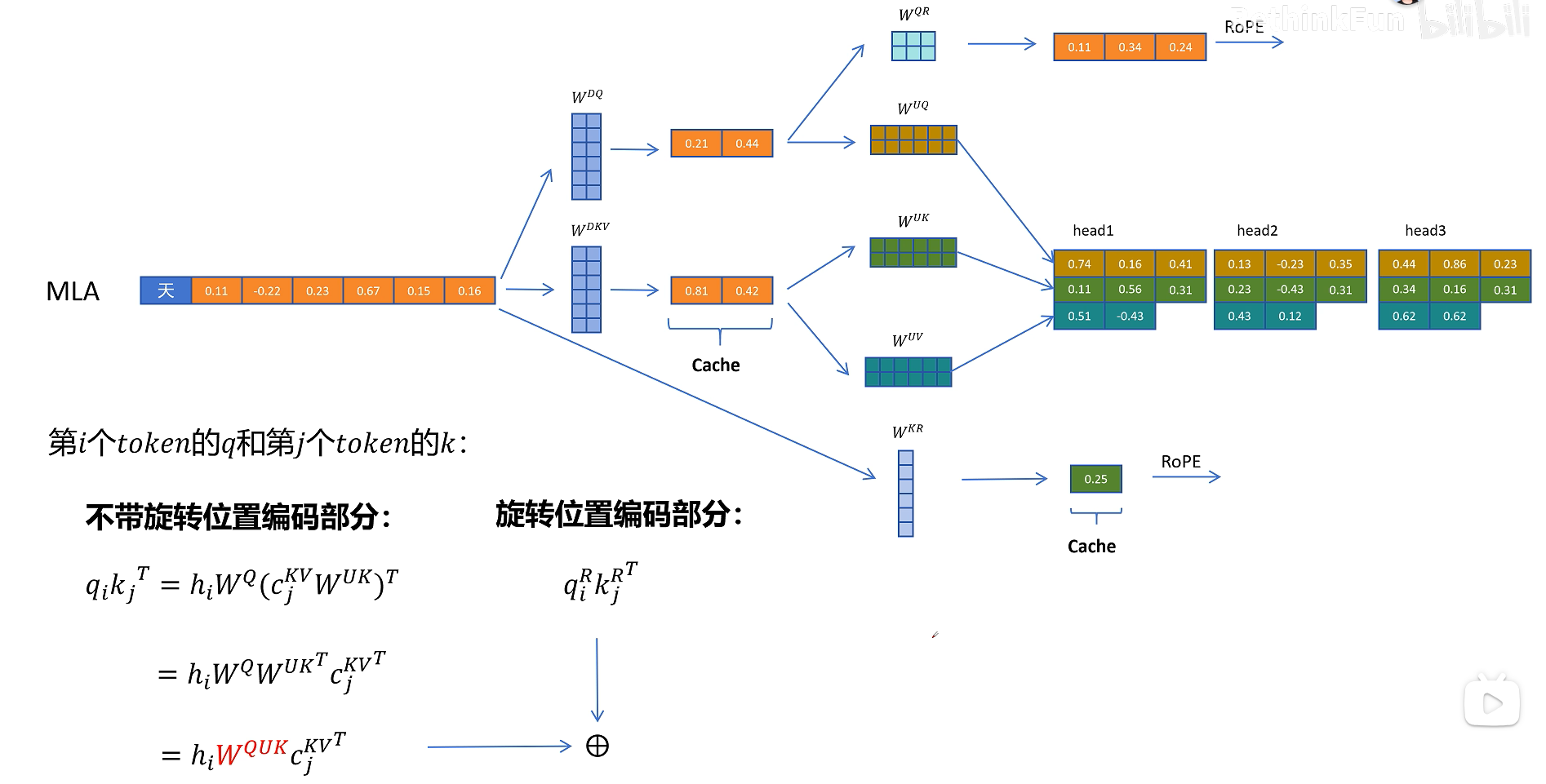 

 到这里终于得到了最终的解决方案，得到了一个既兼容旋转位置编码的压缩KV Cache的方案，同时也可以提升模型的性能。

最后我们来回顾一下论文里面的MLA的图，首先是输入的token特征H，通过它生成压缩的KV特征和压缩的Q向量，然后压缩的KV特征解压为多头的K和V特征，从输入特征H生成多头共享的带旋转位置编码的K_r,再把K_c和K_r合并形成最终带位置编码的K向量。

在看Q向量这边，通过解压生成多头的Q向量，然后从压缩的Q向量生成多头带位置编码的Q_r,

然后合并Q_c和Q_r生成最终带位置编码的Q向量。

接着QKV向量进行多头注意力计算。注意图中阴影部分为需要缓存的中间变量。其中只有KV公用的压缩隐特征和K的多头共享的带位置编码的向量需要缓存。