1. 题目

给你一个整数数组 nums，请你返回该数组中恰有四个因数的这些整数的各因数之和。

如果数组中不存在满足题意的整数，则返回 0 。

示例：
输入：nums = [21,4,7]
输出：32
解释：
21 有 4 个因数：1, 3, 7, 21
4 有 3 个因数：1, 2, 4
7 有 2 个因数：1, 7
答案仅为 21 的所有因数的和。提示：
1 <= nums.length <= 10^4
1 <= nums[i] <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/four-divisors
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

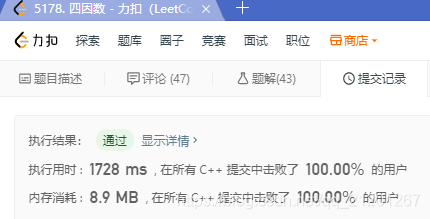
• 直接模拟从2到 n/2，当n很大的时候很耗时

class Solution {
public:int sumFourDivisors(vector<int>& nums) {int sum = 0;pair<bool,int> p;for(int i = 0; i < nums.size(); ++i){p = isfour(nums[i]);if(p.first)sum += p.second;}return sum;}pair<bool, int> isfour(int &n){if(n == 1)return {false, 0};int count = 2;int divs = 1+n;for(int i = 2; i <= n/2; ++i){if(n%i == 0){count++;divs += i;}if(count > 4)return {false,0};}return {count==4,divs};}
};

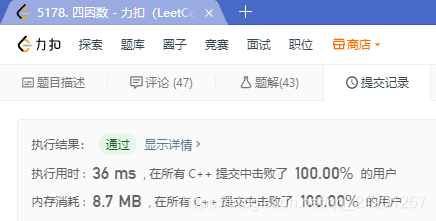
• 由于因数成对出现，所以从2遍历到 $\sqrt{n}$ 即可
• 注意一对因数是相同的情况

class Solution {
public:int sumFourDivisors(vector<int>& nums) {int sum = 0;pair<bool,int> p;for(int i = 0; i < nums.size(); ++i){p = isfour(nums[i]);if(p.first)sum += p.second;}return sum;}pair<bool, int> isfour(int &n){if(n == 1)return {false, 0};int count = 2;int divs = 1+n;for(int i = 2; i <= sqrt(n); ++i){if(n%i == 0){if(i != n/i){count += 2;divs += i+n/i;}else{count += 1;divs += i;}}if(count > 4)return {false,0};}return {count==4,divs};}
};