有限元学习七步流程(系统优化版)
本文先从一维杆的核心力学关系入手,求解其应力、应变;随后介绍位移法的求解思路;在此基础上,引入试函数法,通过虚功原理与最小势能原理建立问题的弱形式;最后,对有限元法的基本计算流程进行总结。
如若希望直接了解整体流程,可跳过前面的PPT内容,从 “① 理论入门:掌握物理本质” 开始观看。
文章目录
- 有限元学习七步流程(系统优化版)
- **① 理论入门:掌握物理本质**
- **② 数学建模:位移与应变的假设**
- **③ 能量法与虚功原理:建立变分关系**
- ⚙️ 虚功原理推导过程
- (1) 虚功方程
- (2) 应变能变化
- (3) 试函数
- (4) 应变能变化计算
- (5) 平衡结果
- ⚙️ 最小势能原理推导
- (1) 最小势能原理
- (2) 系统应变能
- (3) 体系外力势能
- (4) 势能函数
- (5) 取极值条件
- (6) 试函数与结果
- **④ 弱形式与有限元基础**
- **⑤ 有限元离散与矩阵方程**
- **⑥ 数值计算与验证**
- **⑦ 知识融合与高维扩展**
- (1)从一维到二维的推广
- (2)三维问题的拓展
- ✅ **总结**
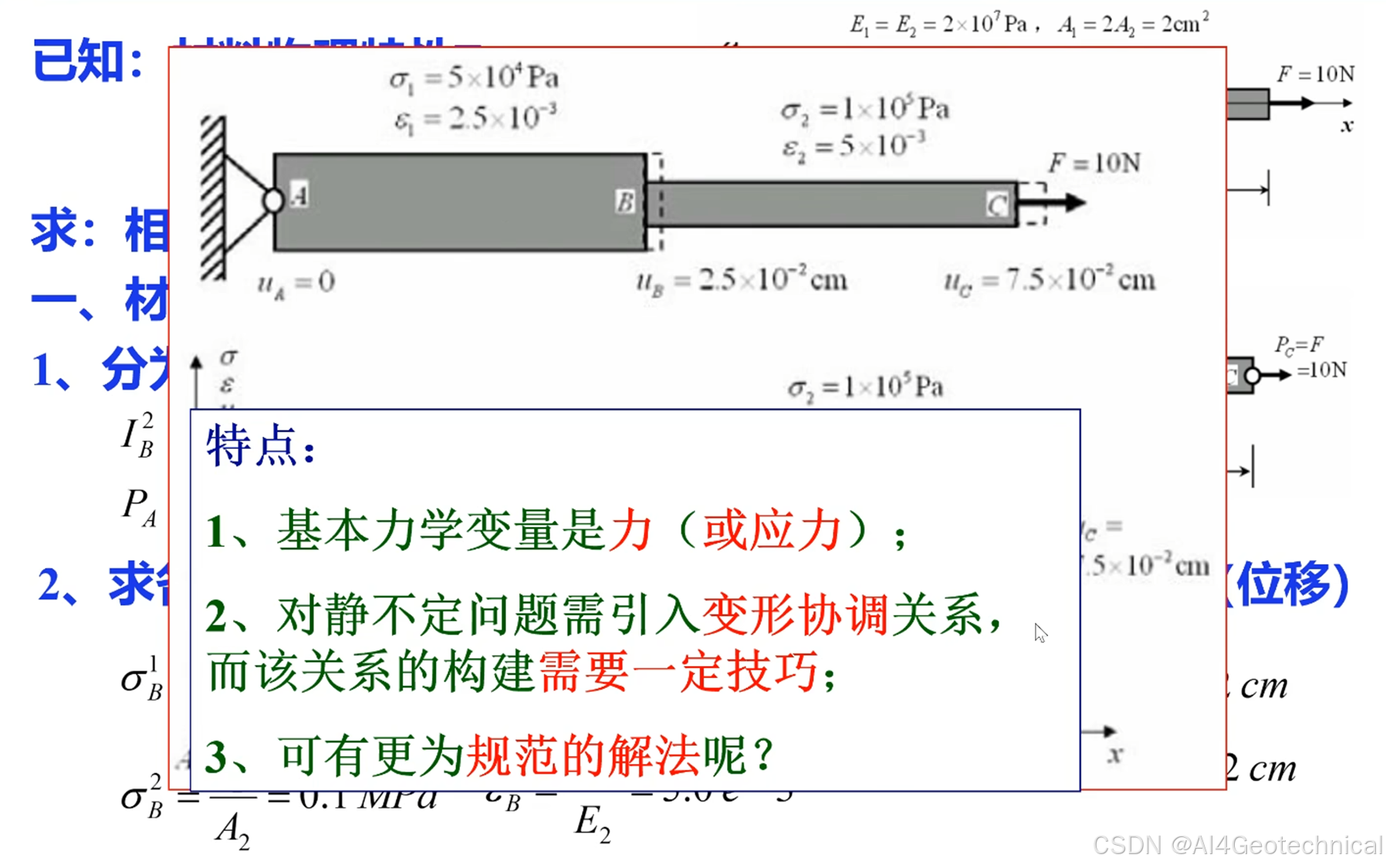
已知: 通过给定的材料属性(如杨氏模量E EE 和截面面积 A AA)和外力 F FF,计算结构在受力下的位移u uu、应变 ϵ \epsilonϵ 和应力 σ \sigmaσ。
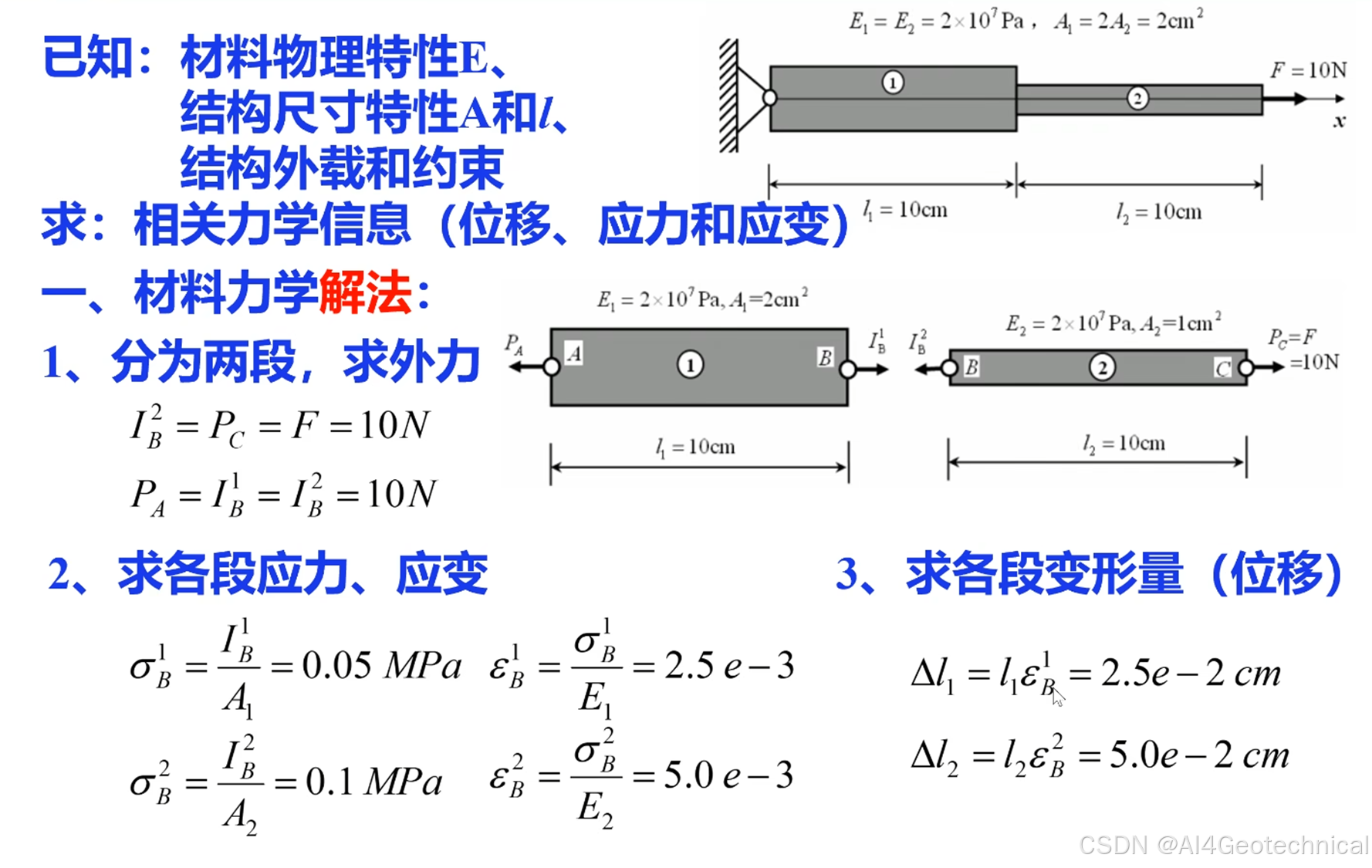
1、传统材料力学求解方法
当结构较为复杂时,采用传统的材料力学方法求解将变得十分繁琐,因此引入了位移法来进行分析。
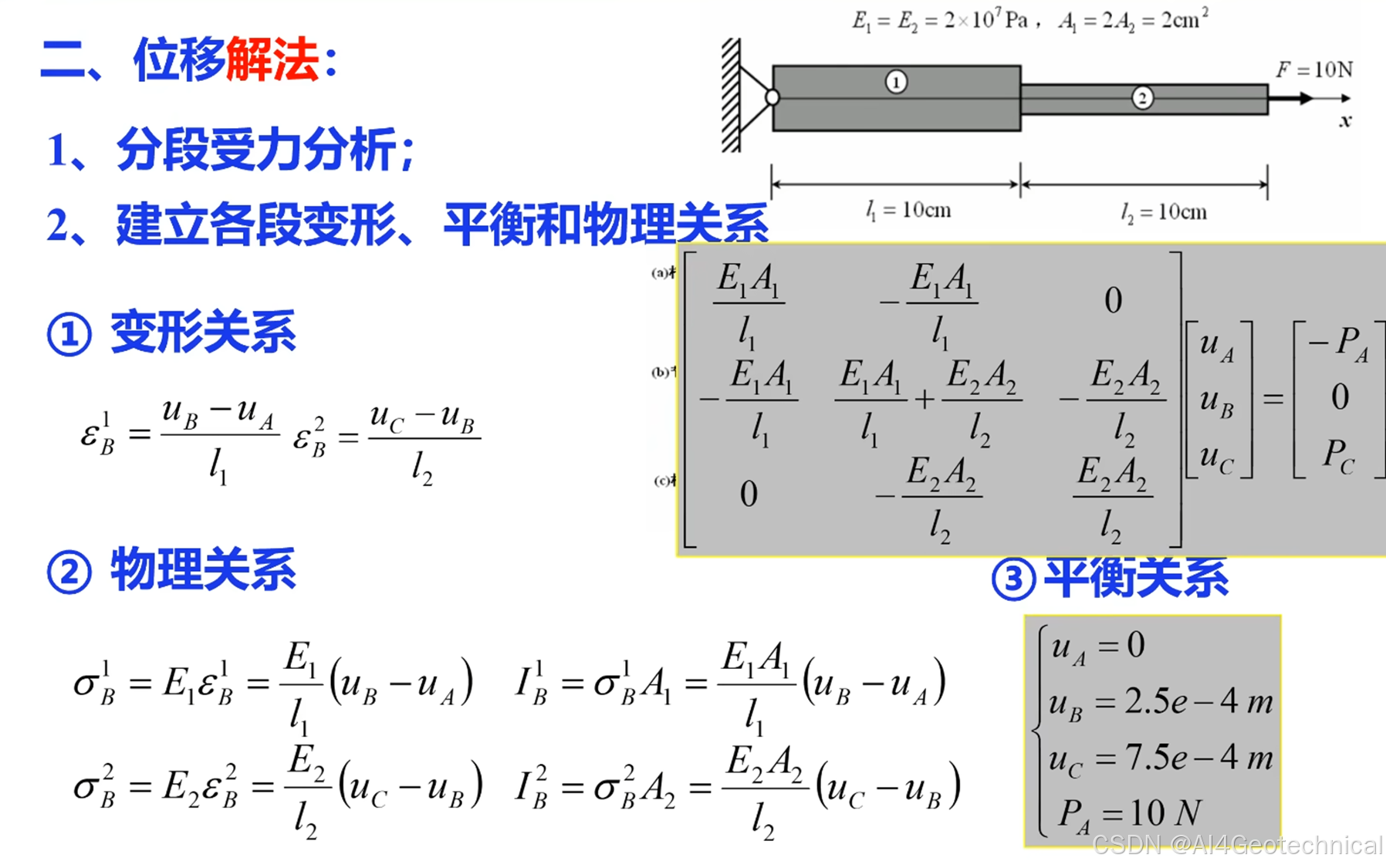
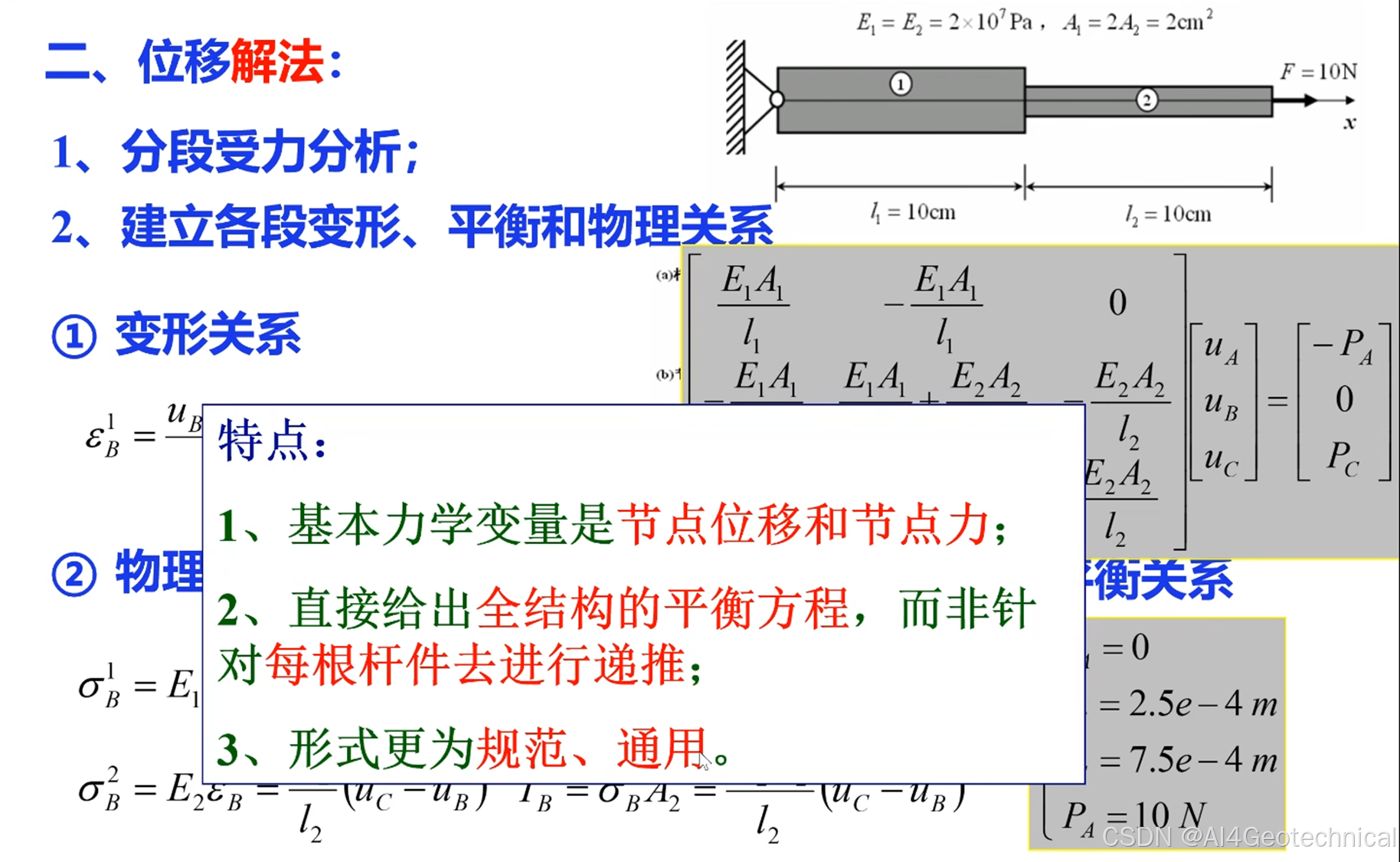
2、位移解法
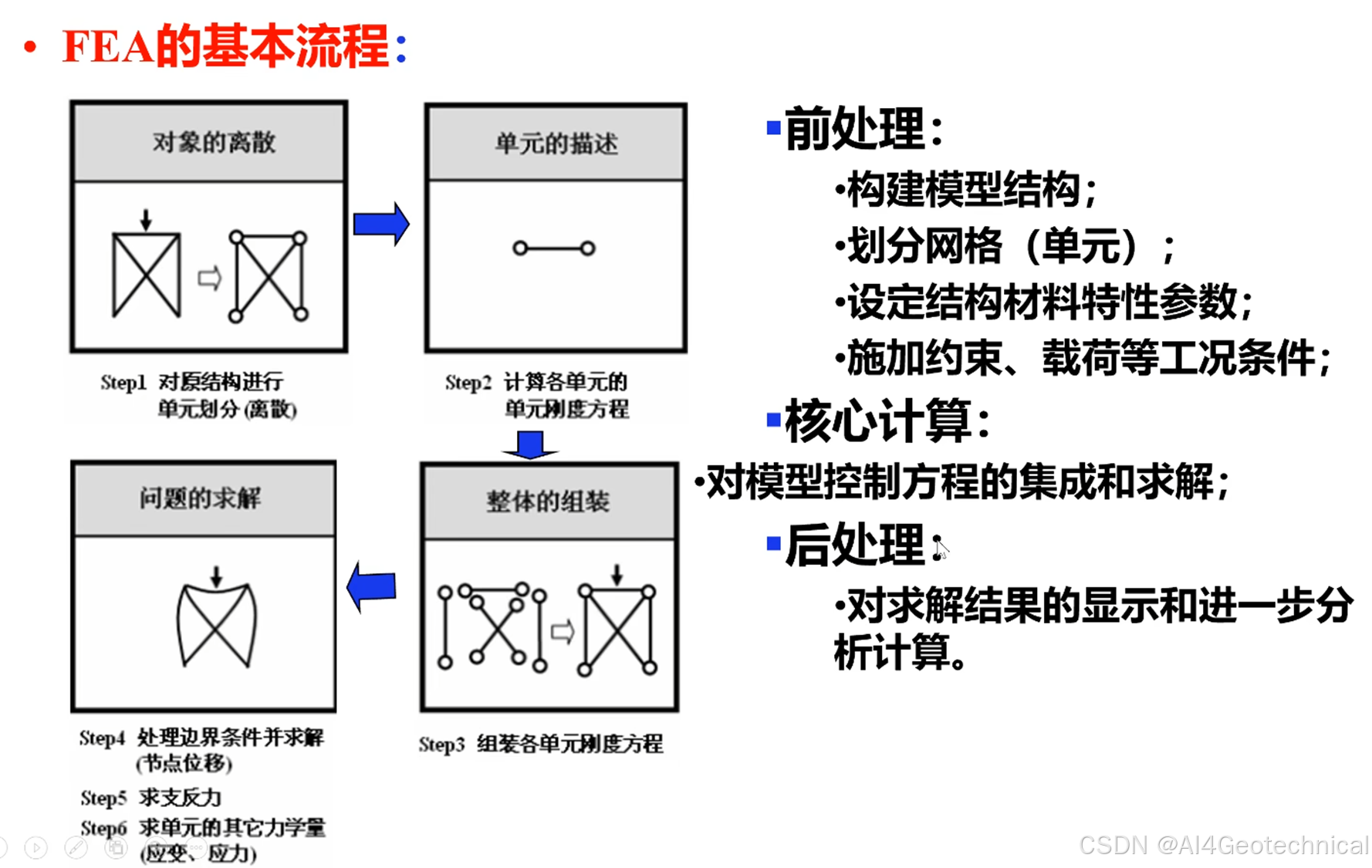
接下来将介绍有限元分析的基本解题流程。
基础流程总结
有限元特点
1️⃣ 力学法的局限
最早的结构分析方法是力学法(位移解法)。
:就是它的基本思路
通过建立平衡方程 + 几何方程 + 本构关系,求解结构的位移、应变和应力分布。
这种方法理论严谨、结果精确,但困难在于——
一旦结构稍微复杂,便会出现高阶偏微分方程。
微分方程不仅难解,而且容易出错,手算几乎不可能。
因此,虽然力学法最精确,却不具备工程可操作性。

2️⃣ 引入能量原理:摆脱微分方程
为了避免直接求解微分方程,人们引入了虚功原理和最小势能原理。
这两个原理是等价的能量法,它们允许我们绕开微分方程,借助积分求解。
核心思想是:
先假设位移函数,再用能量平衡确定未知参数。就是不再直接解微分方程,而
例如:
你能够猜位移是线性的:u ( x ) = a 0 + a 1 x u(x) = a_0 + a_1 xu(x)=a0+a1x
或者猜是正弦的:u ( x ) = b 0 + b 1 sin x u(x) = b_0 + b_1 \sin xu(x)=b0+b1sinx
只要假设满足(或接近)边界条件,就能通过能量原理得到结构响应。
整个过程只涉及积分,不再需要解微分方程!
这就是所谓的:
“从强形式(微分方程)到弱形式(积分方程)”的转变。
具体推导过程可参考链接


虚功原理
最小势能原理
例子
一维
二维
三维
① 理论入门:掌握物理本质
建立力学三大基本关系(以一维杆为例):
平衡方程:
d σ d x + f = 0 \frac{d\sigma}{dx} + f = 0dxdσ+f=0几何关系:
ε = d u d x \varepsilon = \frac{du}{dx}ε=dxdu本构关系:
σ = E ε \sigma = E\,\varepsilonσ=Eε
材料假设:线性弹性、均质、各向同性。
目标:明确应力–应变–位移之间的物理因果关系。
② 数学建模:位移与应变的假设
假设线性位移场:
u ( x ) = c x u(x) = c\,xu(x)=cx边界条件:
u ( 0 ) = 0 u(0) = 0u(0)=0根据力平衡和边界条件:
c = P E A c = \frac{P}{E A}c=EAP因此:
ε = d u d x = P E A , σ = E ε = P A \varepsilon = \frac{du}{dx} = \frac{P}{E A}, \quad \sigma = E\varepsilon = \frac{P}{A}ε=dxdu=EAP,σ=Eε=AP
③ 能量法与虚功原理:建立变分关系
采用势能极值原理:
Π ( u ) = U − W \Pi(u) = U - WΠ(u)=U−W
平衡条件由:
δ Π = 0 ⇒ δ U = δ W \delta \Pi = 0 \quad \Rightarrow \quad \delta U = \delta WδΠ=0⇒δU=δW
对于杆件问题:
u ( x ) = P E A x , ε = P E A , σ = P A u(x) = \frac{P}{E A}x, \quad \varepsilon = \frac{P}{E A}, \quad \sigma = \frac{P}{A}u(x)=EAPx,ε=EAP,σ=AP
⚙️ 虚功原理推导过程
(1) 虚功方程
δ U = δ W \delta U = \delta WδU=δW
(2) 应变能变化
δ W = P ( x ) δ u ( x ) \delta W = P(x)\,\delta u(x)δW=P(x)δu(x)
δ U = δ ( 1 2 ∫ Ω σ ( x ) ε ( x ) d V ) \delta U = \delta \left( \frac{1}{2} \int_{\Omega} \sigma(x)\,\varepsilon(x)\, dV \right)δU=δ(21∫Ωσ(x)ε(x)dV)
(3) 试函数
u ( x ) = c x ⇒ δ u ( x ) = δ c ⋅ x u(x) = c\,x \quad \Rightarrow \quad \delta u(x) = \delta c \cdot xu(x)=cx⇒δu(x)=δc⋅x
σ ( x ) = E ε ( x ) ⇒ δ σ ( x ) = E ⋅ δ c \sigma(x) = E\,\varepsilon(x) \quad \Rightarrow \quad \delta\sigma(x) = E \cdot \delta cσ(x)=Eε(x)⇒δσ(x)=E⋅δc
ε ( x ) = d u d x ⇒ δ ε ( x ) = δ c \varepsilon(x) = \frac{du}{dx} \quad \Rightarrow \quad \delta\varepsilon(x) = \delta cε(x)=dxdu⇒δε(x)=δc
(4) 应变能变化计算
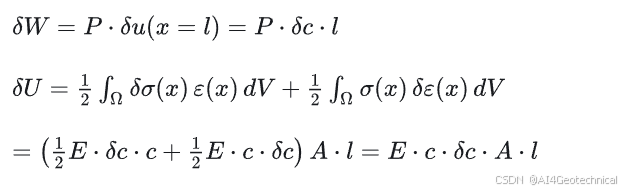
(5) 平衡结果
c = P E A , ε ( x ) = P E A , σ ( x ) = P A , u ( x ) = P E A x c = \frac{P}{E A}, \quad \varepsilon(x) = \frac{P}{E A}, \quad \sigma(x) = \frac{P}{A}, \quad u(x) = \frac{P}{E A}xc=EAP,ε(x)=EAP,σ(x)=AP,u(x)=EAPx
⚙️ 最小势能原理推导
(1) 最小势能原理
min u ( x ) ∈ B C ( u ) [ Π ( u ) = U − W ] \min_{u(x) \in BC(u)} \big[\, \Pi(u) = U - W \,\big]u(x)∈BC(u)min[Π(u)=U−W]
(2) 环境应变能
U = 1 2 ∫ Ω σ ( x ) ε ( x ) d V U = \frac{1}{2} \int_{\Omega} \sigma(x)\,\varepsilon(x)\, dVU=21∫Ωσ(x)ε(x)dV
(3) 系统外力势能
− W = − P ⋅ u ( x = l ) -W = -P \cdot u(x = l)−W=−P⋅u(x=l)
(4) 势能函数
Π ( u ) = 1 2 E c 2 A l − P c l \Pi(u) = \frac{1}{2} E\, c^2\, A\, l - P\, c\, lΠ(u)=21Ec2Al−Pcl
(5) 取极值条件
∂ Π ∂ c = 0 \frac{\partial \Pi}{\partial c} = 0∂c∂Π=0
(6) 试函数与结果
u ( x ) = c x , ε ( x ) = c , c = P E A u(x) = c\,x, \quad \varepsilon(x) = c, \quad c = \frac{P}{E A}u(x)=cx,ε(x)=c,c=EAP
同样得到:
ε ( x ) = P E A , σ ( x ) = P A , u ( x ) = P E A x \varepsilon(x) = \frac{P}{E A}, \quad \sigma(x) = \frac{P}{A}, \quad u(x) = \frac{P}{E A}\, xε(x)=EAP,σ(x)=AP,u(x)=EAPx
④ 弱形式与有限元基础
由强形式(微分方程)通过分部积分得到弱形式:
∫ 0 L E A d u d x d v d x d x = ∫ 0 L f v d x + [ T ˉ v ] L \int_0^L EA \frac{du}{dx}\frac{dv}{dx}dx = \int_0^L f\,v\,dx + [\bar{T}v]_L∫0LEAdxdudxdvdx=∫0Lfvdx+[Tˉv]L
边界条件:
- 本质边界条件:直接作用于位移,如u ( 0 ) = 0 u(0) = 0u(0)=0;
- 自然边界条件:由弱式自动包含,如σ ( L ) = T ˉ \sigma(L) = \bar{T}σ(L)=Tˉ。
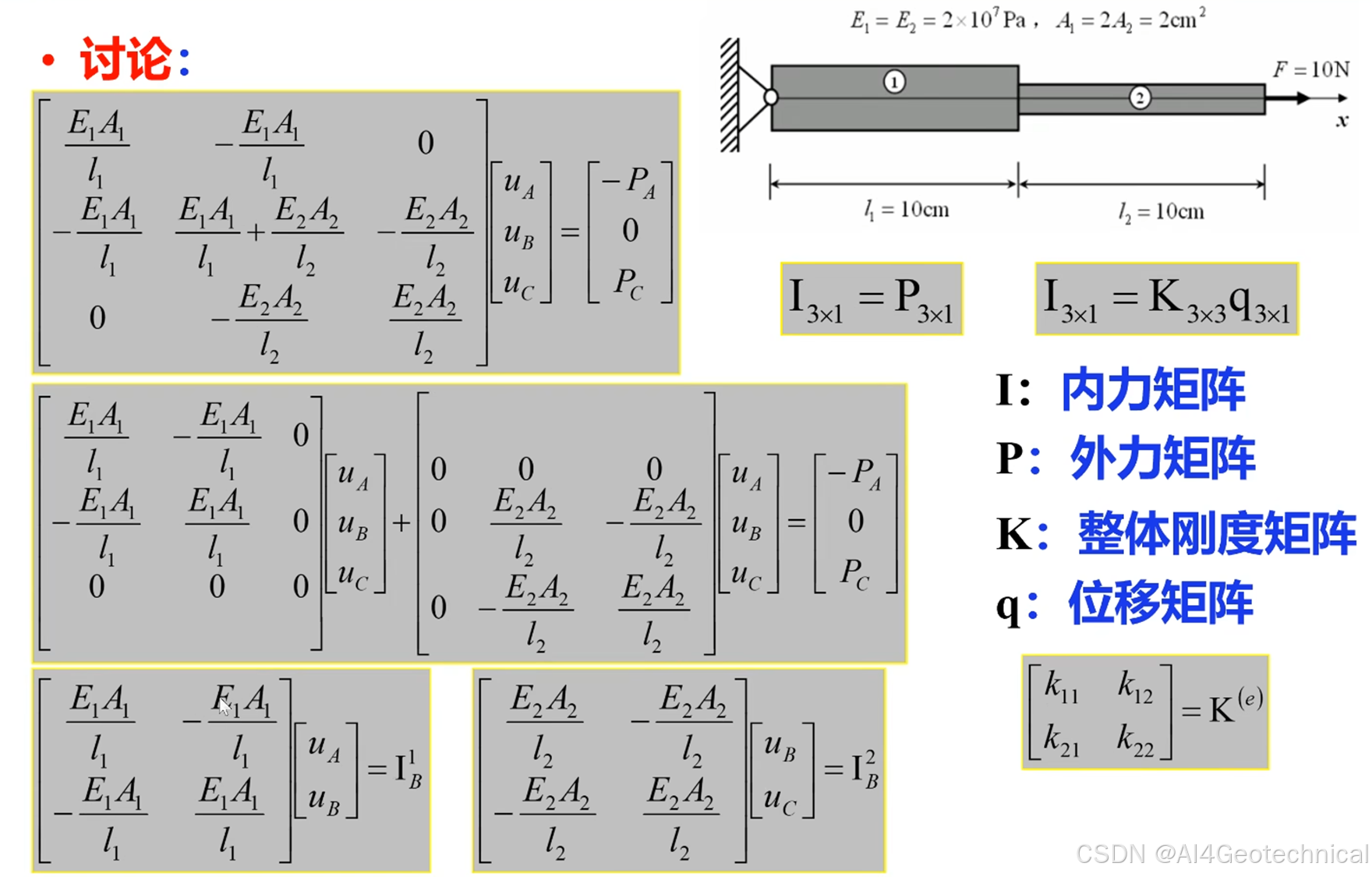
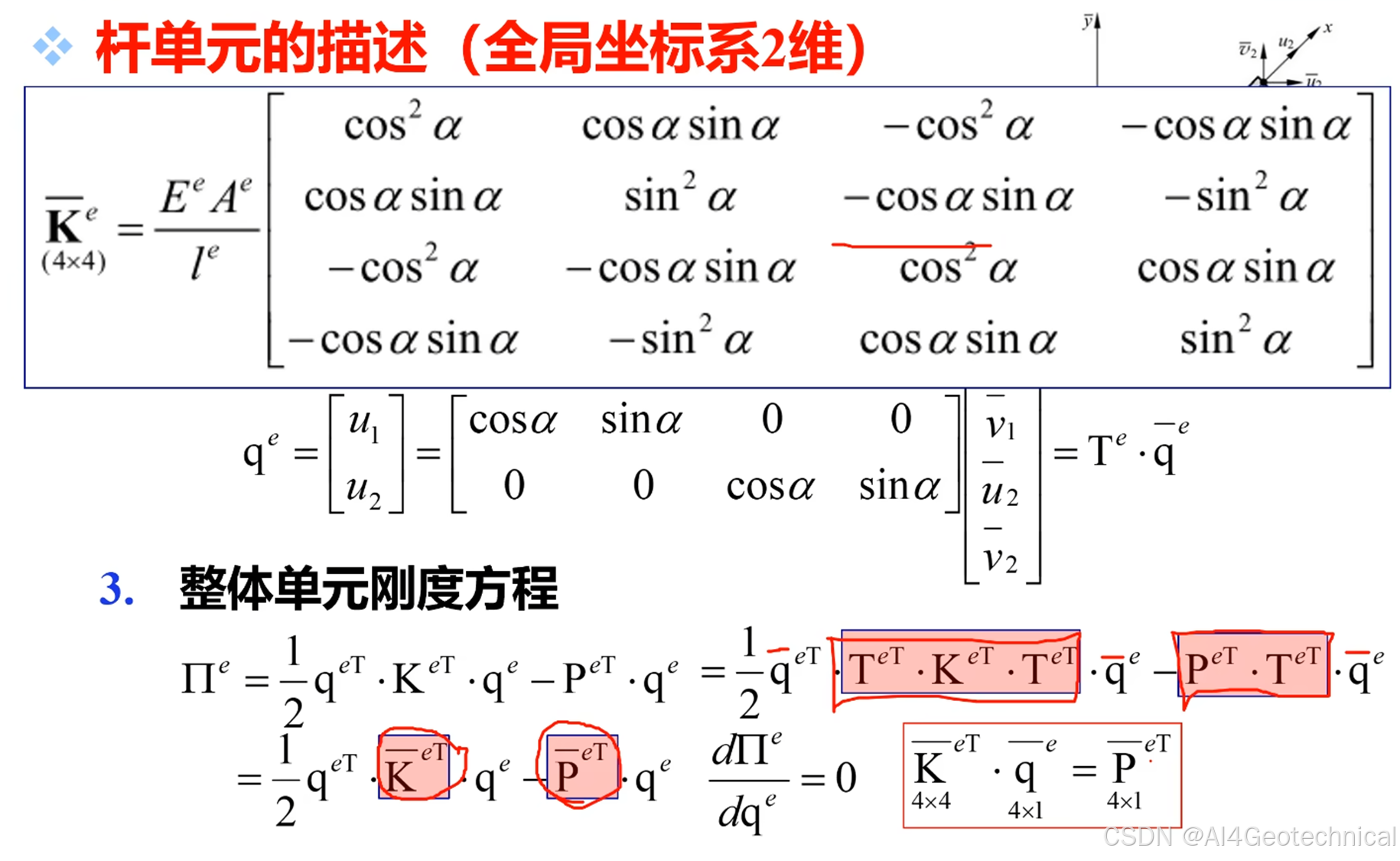
⑤ 有限元离散与矩阵方程
单元内位移近似:
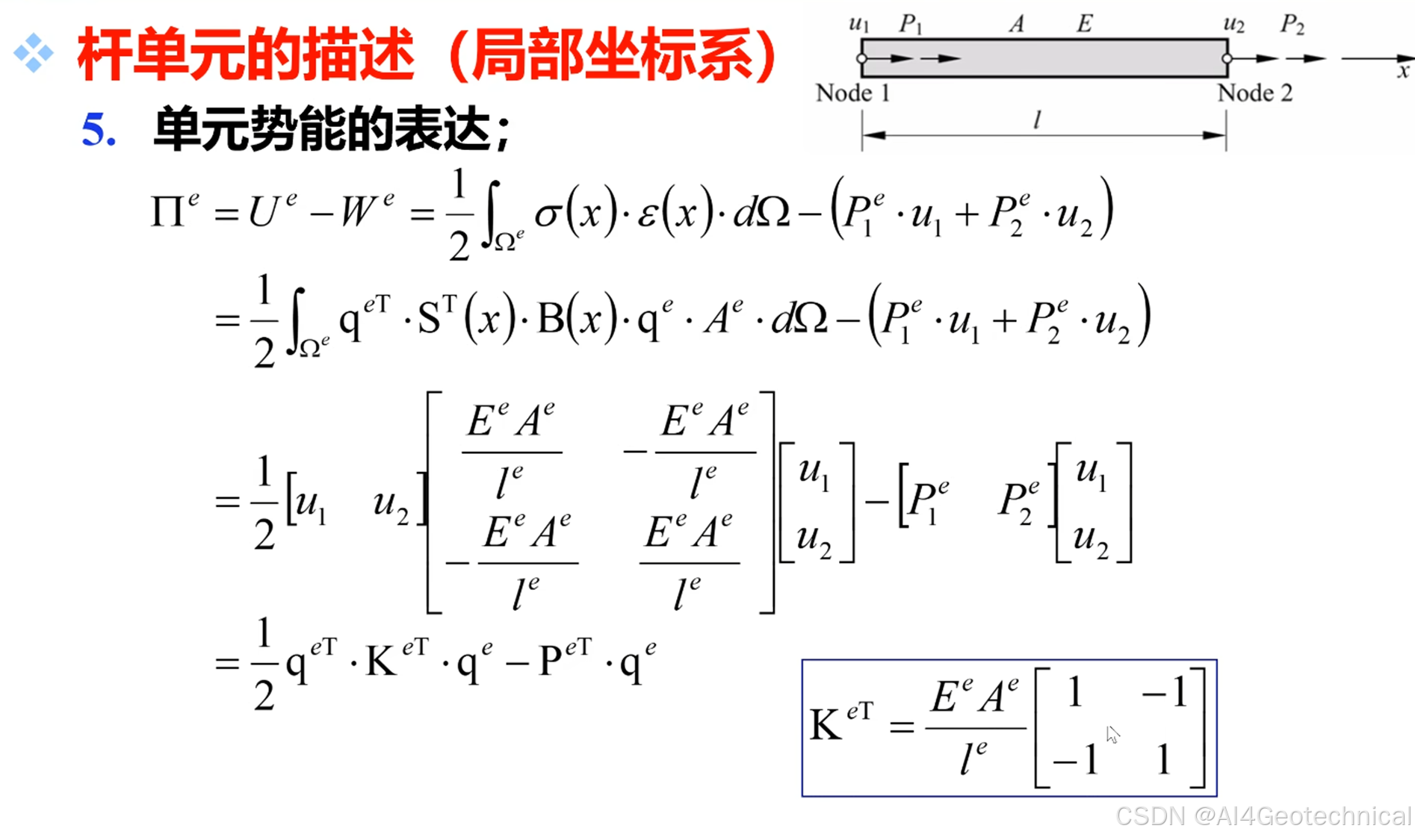
u ( ξ ) = N 1 u 1 + N 2 u 2 , N 1 = 1 − ξ , N 2 = ξ u(\xi) = N_1 u_1 + N_2 u_2, \quad N_1 = 1 - \xi, \; N_2 = \xiu(ξ)=N1u1+N2u2,N1=1−ξ,N2=ξ单元刚度矩阵:
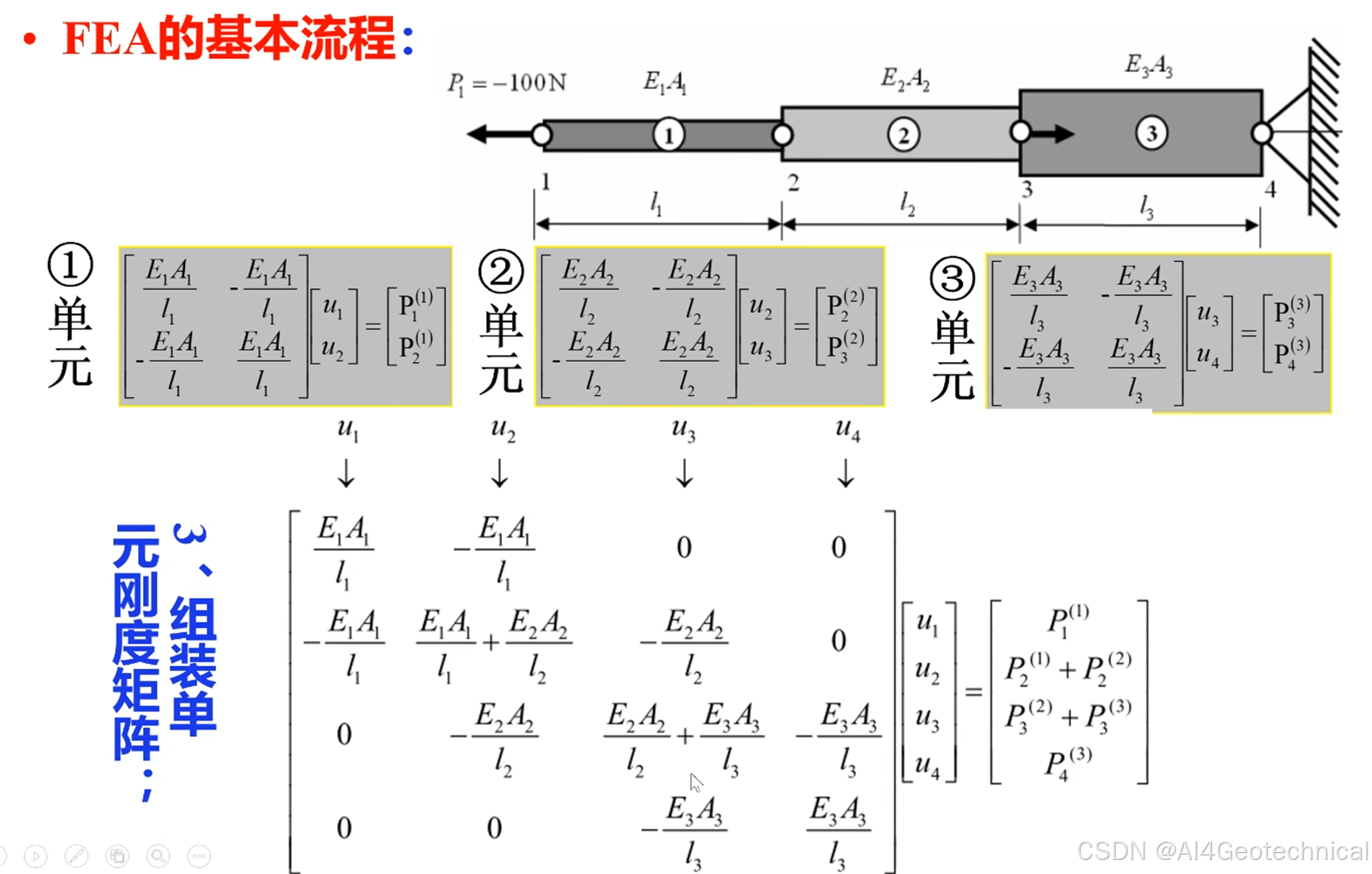
K e = ∫ 0 L B T E A B d x = E A L [ 1 − 1 − 1 1 ] K_e = \int_0^L B^T E A B\,dx = \frac{E A}{L} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}Ke=∫0LBTEABdx=LEA[1−1−11]全局组装:按节点连接关系叠加K e K_eKe形成整体刚度矩阵K KK。
⑥ 数值计算与验证
通过求解线性方程:
K U = F K U = FKU=F
得到节点位移。计算应变与应力:
ε = B U e , σ = E ε \varepsilon = B U_e, \quad \sigma = E \varepsilonε=BUe,σ=Eε与解析解对比,验证有限元解的正确性。
⑦ 知识融合与高维扩展
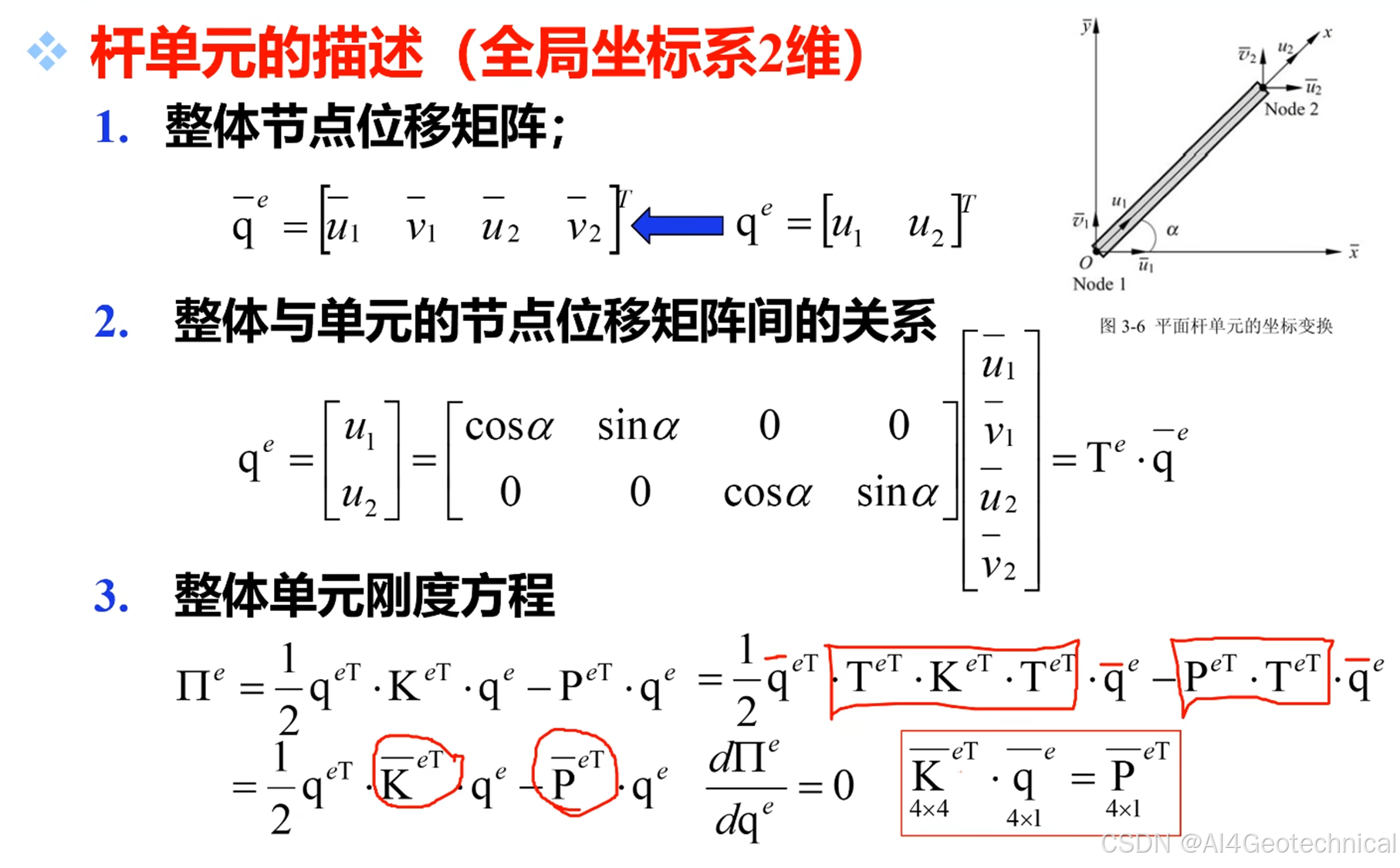
(1)从一维到二维的推广
二维问题常见于平面应力与平面应变状态:
u = u ( x , y ) , v = v ( x , y ) u = u(x, y), \quad v = v(x, y)u=u(x,y),v=v(x,y)
几何方程(应变–位移关系):
ε x = ∂ u ∂ x , ε y = ∂ v ∂ y , γ x y = ∂ u ∂ y + ∂ v ∂ x \begin{aligned} \varepsilon_x &= \frac{\partial u}{\partial x}, \\ \varepsilon_y &= \frac{\partial v}{\partial y}, \\ \gamma_{xy} &= \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \end{aligned}εxεyγxy=∂x∂u,=∂y∂v,=∂y∂u+∂x∂v
矩阵形式:
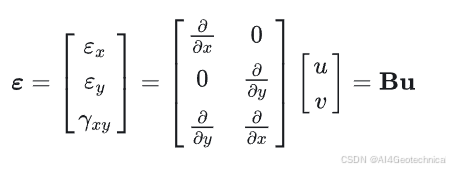
平面应力本构关系:
D plane-stress = E 1 − ν 2 [ 1 ν 0 ν 1 0 0 0 1 − ν 2 ] \mathbf{D}_{\text{plane-stress}} = \frac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \frac{1-\nu}{2} \end{bmatrix}Dplane-stress=1−ν2E1ν0ν100021−ν
平面应变本构关系:
D plane-strain = E ( 1 − ν ) ( 1 + ν ) ( 1 − 2 ν ) [ 1 ν 1 − ν 0 ν 1 − ν 1 0 0 0 1 − 2 ν 2 ( 1 − ν ) ] \mathbf{D}_{\text{plane-strain}} = \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 & \frac{\nu}{1-\nu} & 0 \\ \frac{\nu}{1-\nu} & 1 & 0 \\ 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{bmatrix}Dplane-strain=(1+ν)(1−2ν)E(1−ν)11−νν01−νν10002(1−ν)1−2ν
二维单元刚度矩阵:
K e = ∫ V B T D B d V \mathbf{K}_e = \int_V \mathbf{B}^T \mathbf{D} \mathbf{B}\, dVKe=∫VBTDBdV
(2)三维问题的拓展
三维位移场:
u = u ( x , y , z ) , v = v ( x , y , z ) , w = w ( x , y , z ) u = u(x,y,z), \quad v = v(x,y,z), \quad w = w(x,y,z)u=u(x,y,z),v=v(x,y,z),w=w(x,y,z)
应变分量: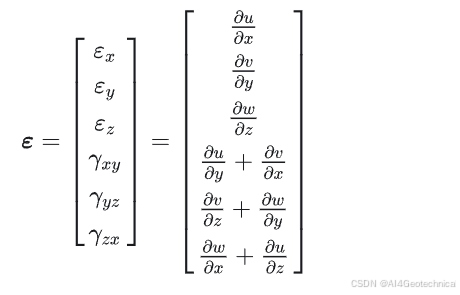
三维线弹性本构矩阵:
D 3 D = E ( 1 − ν ) ( 1 + ν ) ( 1 − 2 ν ) [ 1 ν 1 − ν ν 1 − ν 0 0 0 ν 1 − ν 1 ν 1 − ν 0 0 0 ν 1 − ν ν 1 − ν 1 0 0 0 0 0 0 1 − 2 ν 2 ( 1 − ν ) 0 0 0 0 0 0 1 − 2 ν 2 ( 1 − ν ) 0 0 0 0 0 0 1 − 2 ν 2 ( 1 − ν ) ] \mathbf{D}_{3D} = \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 & \frac{\nu}{1-\nu} & \frac{\nu}{1-\nu} & 0 & 0 & 0 \\ \frac{\nu}{1-\nu} & 1 & \frac{\nu}{1-\nu} & 0 & 0 & 0 \\ \frac{\nu}{1-\nu} & \frac{\nu}{1-\nu} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{bmatrix}D3D=(1+ν)(1−2ν)E(1−ν)11−νν1−νν0001−νν11−νν0001−νν1−νν10000002(1−ν)1−2ν0000002(1−ν)1−2ν0000002(1−ν)1−2ν
三维单元刚度矩阵:
K e = ∫ V B T D 3 D B d V \mathbf{K}_e = \int_V \mathbf{B}^T \mathbf{D}_{3D} \mathbf{B}\, dVKe=∫VBTD3DBdV
典型单元包括四面体、六面体、棱柱体等,通过三维高斯积分计算。
✅ 总结
一维问题奠定理论基础,二维与三维扩展实现真实工程模拟。
:就是其核心始终
“几何方程 + 本构关系 + 平衡方程 → 弱形式 → 数值离散”












-F:\硕士阶段\Java\课程代码\后端\web-ai-code\web-ai-project02\tlias-web-management)









 day21 - 二叉树part8)






