论文导读：从 TSMC ISSCC 看 SRAM 存算发展

上次集中学习存算工作还是一年半以前，时光如梭，SRAM CIM 范式对比记忆又有新花样。本篇 blog 针对 ISSCC 2024 34.4 TSMC 的 3 nm 数字 SRAM 近存算 Macro 个例分析，并结合架构视角谈谈个人感触^[1]。

RAM 的物理-逻辑映射形式化表示

ISSCC CIM Session 相比 Accelerator Session 显得“稀疏”许多，而 TSMC 的文章更是“惜字如金”，文字和结构都是能省尽省，有一定阅读门槛。因此在引入文章前，有必要补充一下 SRAM Macro 的形式化描述，用一种符号化、规范化的语言表达 Macro 的物理-逻辑结构映射关系。SRAM 属于 RAM 的一种，以下分析对所有 RAM 都应是大致适用的。

RAM 包含两个层面的定义：

• 物理结构：传统使用阵列 (Array) 即行和列交织的结构组织 cell 进行布局，这是一个二维结构 [Row, Col] ，各类技术比如 Column Multiplexing, Flying BL 等会对这两个维度做进一步切分，但不会脱离二维的组织范畴。
• 逻辑结构：即对外暴露出来的逻辑接口，传统也是一个二维结构 [Depth, Bitwidth] ，Depth 维度在时间上串行访问，而 Bitwidth 维度在并行访问。

用多维张量的思想定义了物理-逻辑维度，不妨继续借用爱因斯坦标记法^[2]定义二者映射关系，所谓物理-逻辑映射，即是以下维度变换关系：

\[\underset{\text{Physical}}{[\text{Row}, \text{Col}]} \longrightarrow \underset{\text{Logical}}{[\text{Depth}, \text{Bitwidth}]} \]

举个例子，比如一个 64 行，64 列的阵列，列上使用 Column Multiplexing 拆分为 16 x 4 ，每次通过 Col Decoder 选择 64 列中的 16 列交互。则其物理-逻辑映射关系为 ：

\[[r, (cx,c)]\rightarrow [(cx, r), c] \]

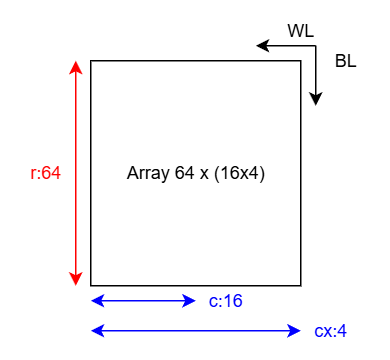
cell 数量为各维度乘积 \(cell=cx\times r \times c\) , bitwidth 为 \(c\)，depth 为 \(cx\times r\)。正如之前 blog 所说^[3] —— RAM 是一种通过牺牲在 depth 上的并行读取从而节约读写外围电路面积开销进而实现高密度存储数据的结构，以时间换空间。体现在参数上，即是 cell 数量（或称为存储内部带宽）和 bitwidth (存储 IO 带宽) 的不对称，RAM 的高密度和 IO 不对称二者来源同一；体现在电路上，则是超长的 Bit Line 以及为了防止读出时 cell 驱动超长的 Bit Line 破坏稳态，采用微扰动以及 Sense Amplifier 结构捕捉变化。

特殊技术分析

结合论文，具体分析存算使用的特殊技术以及如何用上述方法表示。TSMC 架构图如下，注意34.4.2 右侧电路图（1） 省略了 cell 结构，cell 仍然使用 6 T 结构，（2）本图相比一般画法转置了一下，BL 方向为横向，后续 Row 和 Col 术语仍然是按前文语义分析而非图转置结构。

读写异构

读和写的逻辑并一致。可能由于存储介质特性导致，比如 ReRAM 写慢读快；有些是特殊架构需求，广义上来说 CIM 如果不考虑重构为纯 Buffer 的需求，其相对于读出计算单元则是读出，高读带宽低写带宽。

一般来说读写异构有两个用途

• 读写带宽不一致，从架构特性上 Data-Locality 理论上仅存在“高读带宽-低写带宽”的设计，从存储介质上来看目前也主要是“高读带宽-低写带宽”
• 重构 cell 组织 layout。

比如论文中写入带宽是读出带宽的 1/4，解释理由是方便布线： “Moreover, only one WL in a macro is selected and 4:1 multiplexer is used in the LIO write circuitry to mitigate routing congestion”。

Local IO 以及存算异构

Local IO 中的 IO 是相对于计算单元而非整体存算 macro 而言。前文提到 “存储内部高带宽- IO 低带宽”是 RAM 的底层逻辑，而 SRAM CIM 就是利用 GEMM 中 reduce 操作，在存储内进行 reduce 将低带宽的 reduce 结果 （partial sum）暴露到 IO，从而完成算法-架构的映射。换言之，乘加器输入利用的是存储内带宽，怎么会和 IO 概念扯上联系呢？

这不得不提一个存算比的概念，其实看早期 SRAM CIM 如果不考虑“存算-存储”功能重构只作为存算模块存在，是不存在 SA 结构的，存储单元和乘法单元的配比是 1：1 ，乘法器输入带宽完全对应存储内带宽^[4]，每个 cell 有根单独连线连接乘法器。

而 TSMC 这篇文章实际是 18 个 row 复用一个乘法器，存储到计算连线是 “cell->bitline -> latch -> LIO -> logic”，需要经过一根公共的 bitline 读出。存储单元和乘法单元的配比是 18:1，即存算比提高了。对于每 18 行的小 segmentation 来说，便是通过相对低带宽的 IO 读出。如果非要定义血缘，这类计算应该算“近存计算”，cell 和 logic 再次被 local IO 隔开。不同路线数字 SRAM 存算定义如下：

路线	cell 对乘法器比例	特点
存算一体	= 1	不存在共用结构，cell 和计算直接连接
近存算	> 1	local IO 隔开 cell 和计算，相当于将多个小 SRAM 和 logic 一起做后端，以 Macro 形态整体交付
传统存算分离	>> 1	IO 隔开 cell 和计算

近存算虽然本质拓扑上和传统存算分离一致，但参数变化也会导致电路设计收敛到不同的设计选项，比如文章中提到由于 BL 很短，删除了 SA ，“We eliminated sense amplifiers because there are only 18 Rows in each segment and the BL discharge period is short. This simplifies the read path In LIO circuitry and minimizes the area and read energy ”，读出路径改为了一个反馈电路（猜测是 full-swing）和单边非差分的锁存器结构。

这篇工作存储部分使用了高电压+hvt ，而计算部分使用低电压 +lvt，存储和计算是电压域异构设计。SRAM 和 logic 的器件特性存在差异，随着节点缩放，SRAM 面积缩放落后于 logic^[5]。我猜测 IDEM 2022 的报告是在相同电压下提取 SRAM Macro 和逻辑的数据，SRAM 牺牲额外的面积应该是为了换取时序性能，即 SRAM 的延时特性是劣于 logic 的，也许是因为 SRAM 超长的 BL？此处电压域异构设计应该是匹配 SRAM 和 logic 的时序特性。

Flying BL

和 Column Multiplexing 原理思路类似，传统派 BL 都是并排摆放，为了布局方便将一对 Segmentation 上下摆放，即图中的 Top 和 Bottom 结构。

ISSCC 24 34.4 的形式化描述

Macro 有 18 个 segments ，每个 segment 结构是个小 SRAM 可以单独控制，需要将上述公式添加一维扩展到多个 SRAM ：

\[\underset{\text{Physical}}{[\text{Seg},\text{Row}, \text{Col}]} \longrightarrow \underset{\text{Logical}}{[\text{Seg},\text{Depth}, \text{Bitwidth}]} \]

• 总 cell 数量是 \(\text{Seg}\times \text{Depth} \times \text{Bitwidth}\)
• 总控制选择信号数量是 \(\text{Seg}\times \text{Depth}\)
• 最大读出带宽是 \(\text{Seg}\times \text{Bitwidth}\)

注意 Seg 维度同时分配到选择信号和读出带宽信号上，这似乎和前文“串行 Depth-并行 Bitwidth” 思想矛盾。这里代表一种 reconfigurable 能力，既可以充分利用控制信号以小粒度读写带宽交互，也可以充分利用带宽，而此时减少控制信号自由度。多 SRAM 的这种控制特性和 Byte Enable 信号本质是一样的。

而在布局上， Seg 其实同时映射到行（2，flying bl）和列（9，跟据 34.4.1 画法推测），Row 和 Col 变量实际指一个 Seg 内的物理结构。

ISSCC 34.4 存算的形式化描述如下：

\[\begin{align} \text{Read}: [s,r,(ci,co,c)]&\rightarrow[s,r,(ci,co,c)]\\ \text{Write}: [s,r,(ci,co,c)]&\rightarrow[s,(r,ci),(co,c)] \end{align} \]

各变量数值和含义如下

符号	数值	含义
s	18	Segments 的数量
r	18	行数量
ci	4	映射到 Ch In 维度, 也是写入的 4:1 Mux
co	4	映射到 Ch Out 维度
c	12	写入粒度 12 bit

如果补充完整的计算结构映射，对于 GEMM 维度 \([T, C_{in}, C_{out}]\) 以及单位精度 \(P\) SRAM CIM 做 weight stationary，故只有 weight 相关维度 \([C_{in}, C_{out},P]\)。

\[\underset{\text{Physical}}{[\text{Seg},\text{Row}, \text{Col}]} \longrightarrow \underset{\text{Logical}}{[\text{Seg},\text{Depth}, \text{Bitwidth}]}\longrightarrow \underset{\text{GEMM}}{[\text{C}_{in}, \text{C}_{out},\text{P}]} \]

本篇工作表达式为：

\[\text{Read}: [s,r,(ci,co,c)]\rightarrow[s,r,(ci,co,c)] \rightarrow[(s,ci),co,c] \]

这里 GEMM 表示的是空间维度，即一个周期读出数据，故时间维度的 r 没有体现最后的维度，此维度可跟据需要选择映射到输入或输出维度之上。

---

1. https://ieeexplore.ieee.org/document/10454556 ↩︎

2. https://github.com/arogozhnikov/einops ↩︎

3. https://www.cnblogs.com/devil-sx/p/19097688 ↩︎

4. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9931922 ↩︎

5. https://fuse.wikichip.org/news/7343/iedm-2022-did-we-just-witness-the-death-of-sram/ ↩︎