前言
笔者从2025.4.22第一次通过线段树模板,至今也不过半年时间,虽然短暂,但是却让其成为了笔者最喜欢的算法,因此,我常常会大喊我是线段树的狗。为了帮助自己记忆以及造福后人,笔者提键盘写出了这篇文章。——2025.10.29
为什么要学线段树
我认为线段树是世界上最好用的数据结构,没有之一!!!
当然,我直接这么说你是肯定不信的,让我们看看线段树都能干什么。
对于一颗线段树,它能支持:在单次时间复杂度为 \(O(\log n)\) 的情况下进行区间修改,查询。
Q:没了?
A:对,没了。
那我学个蛋,跑路了。
等等先别走,那我问你,你暴力对一个数组进行区间修改的最坏时间复杂度是不是 \(O(n)\) 的?
你说是?但是线段树可以 \(O(\log n)\) 啊,这难道真的不值得你学一下吗?
你说不值得?
我**%#*#%#
算了,闲话少说,让我们进入正题。
关于线段树的介绍
线段树长什么样?
长这样
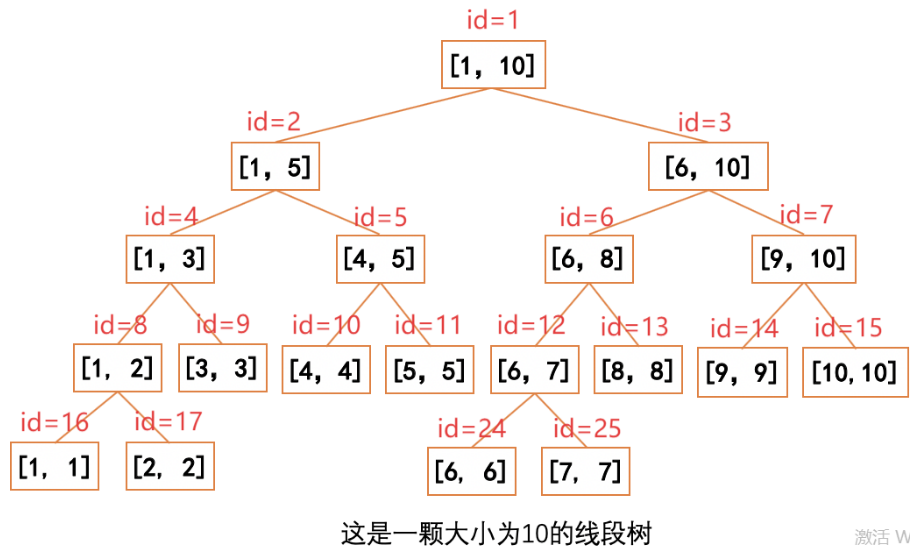
这张图是什么意思呢?
每个方格代表一个线段树的节点。
每个节点上面的 \(id\) 代表这个点的编号。
而节点中写的 \([L,R]\) 则代表这个节点维护下标范围在 \(L\sim R\) 的区间。
例如编号为 \(5\) 的节点维护的是下标为 \(4\sim 5\) 的区间。
由观察可以得到,对于一个节点,如果它维护的区间 \([L,R]\) 满足 \(L\ne R\) 那么它一定会有两个儿子节点(我们将其称作左儿子和右儿子),如果这个点的编号为 \(id\),那么它的左儿子的编号为 \(id\times 2\),右儿子的编号为 \(id\times 2+1\)。
它的左儿子维护的区间为 \([L,\lfloor \frac{L+R}{2}\rfloor]\)。
它的右儿子维护的区间为 \([\lfloor \frac{L+R}{2}\rfloor+1,R]\)。
知道这些基础概念之后我们就可以尝试实现一颗线段树了。
*注:下文中的 \(L,R\) 均代表当前线段树节点维护的区间的左右端点,\(mid\) 均代表 \(\lfloor \frac{L+R}{2}\rfloor\),\(l,r\) 代表查询区间(此限制对代码内的变量仍然适用)。
线段树的简单实现
我们首先要建树,现在假设我们维护长度为 \(n\) 的数组 \(a\) 的区间和。
建树
void make_tree(int L,int R,int id){if(L==R){//到达叶子结点,没有左右儿子tree[id].sum=a[L];//直接赋值return ;//退出建树函数}int mid=(L+R)>>1;make_tree(L,mid,id<<1);//递归左儿子make_tree(mid+1,R,id<<1|1);//递归右儿子tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;//当前节点维护的区间和使用左右儿子来得到。
}
区间查询
还是刚才的图片

假设现在我们要查询区间 \([2,7]\)。
那我们的答案就应用 \(id={17,9,5,12}\) 得出。
怎么实现?
我们先给代码,根据代码里面的注释进行理解。
int query(int l,int r,int L,int R,int id){if(l<=L&&r>=R) return tree[id].sum;//如果当前节点区间完全被查询区间包含,直接返回int mid=(L+R)>>1,ans=0;if(l<=mid) ans+=query(l,r,L,mid,id<<1);//如果当前区间有一部分落在在左儿子,那么递归左儿子,并将答案增加 if(r>mid/*写成r>=mid+1也可以*/) ans+=query(l,r,mid+1,R,id<<1|1);//如果当前区间有一部分落在在右儿子,那么递归右儿子,并将答案增加 return ans;//返回答案
}
现在问题来了,如何证明这个函数是 \(O(\log n)\) 的,相信大多数初学者甚至已经学会线段树较长时间的人都不能给出一个比较完整的证明。
笔者在这里给出一个自己推出的证明方式。
首先要明确的是一颗线段树的深度是 \(\log n\) 的。
深度每增加一层,维护的区间长度会除以 \(2\)。
这个很好理解。
假设查询区间为 \([l,r]\)。
显然我们第一次调用函数一定会先访问节点编号为 \(1\) 的节点。
我们进行分类讨论:
- 情况 \(1\):
当 \(l=1\)。
如果 \(r>mid\) 那么会同时递归左右儿子,而左儿子由于被完全包含会直接在被访问时 \(return\) 掉,而递归右儿子时又会面对查询区间的右端点小于等于当前节点维护的右端点的情况,于是这个节点就会面对和它的父亲相同的情况。
如果 \(r<=mid\) 则只会递归左儿子,之后的情况就是 \(r>mid\) 的简易版了。
此时线段树的每层最坏会有两个节点被访问,时间复杂度 \(O(2\times\log n)\)。
- 情况 \(2\):
当 \(r=n\)。
基本同上,不解释。
- 情况 \(3\):
当 \(l\le mid\le r\)
我们会递归左右儿子,此时左儿子会退化成情况 \(2\),右儿子会退化成情况 \(1\)。
线段树的每层最坏会有四个节点被访问,时间复杂度 \(O(4\times\log n)\)。
- 情况 \(4\):
当 \(l\le r\le mid\)
递归左儿子,在多次递归后迟早会退化成情况 \(1\) 或情况 \(2\) 或情况 \(3\)。
线段树的每层最坏依旧会有四个节点被访问,时间复杂度 \(O(4\times\log n)\)。
- 情况 \(5\):
当 \(mid<l\le r\)
基本同上,不解释。
证毕。
可能写的比较抽象,但是没关系,其实你只需要知道线段树是单次查询 \(O(\log n)\) 的即可(对,其实你不明白也问题不大,但是我还是写了,也是因为笔者也因这个问题困惑了一段时间)。
区间查询就先到这里,现在就要讲修改了。
单点修改
其实学会查询后修改就没什么好说的了,直接上代码。
void add(int l,int k,int L,int R,int id){if(L==R){//到达修改的点tree[id].sum+=k; return ;}int mid=(L+R)>>1;if(l<=mid) add(l,k,L,mid,id<<1);//修改的点在左儿子 else add(l,k,mid+1,R,id<<1|1);//否则一定在右子树 tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;//不要忘记用儿子更新自己
}
这个代码的时间复杂度很好证明,线段树的每层一定会有一个节点被访问,时间复杂度 \(O(\log n)\)。
现在我们就可以 \(AC\) P3374 【模板】树状数组 1了。
但是为什么是单点修改,不是区间修改吗,退钱!!!



离线安装失败的问题解决)















