Paper Reading: Symbolic Regression Enhanced Decision Trees for Classification Tasks

目录

• 研究动机
• 文章贡献
• 本文方法
• 实验结果
  • 合成数据集实验
  • 真实数据集
  • 噪声数据测试
  • 可解释分析
• 优点和创新点

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况	详细
标题	《Symbolic Regression Enhanced Decision Trees for Classification Tasks》
作者	Kei Sen Fong, Mehul Motani
发表会议	The Thirty-Eighth AAAI Conference on Artificial Intelligence (AAAI-24)
发表年份	2024
会议等级	CCF-A
论文代码	文中未公开

作者单位：

1. Department of Electrical and Computer Engineering, National University of Singapore
2. N.1 Institute for Health, Institute for Digital Medicine (WisDM), Institute of Data Science, National University of Singapore

研究动机

传统决策树在表格分类任务中虽然具有出色的可解释性优势，但在处理复杂决策边界时存在显著局限性。同时固有的轴平行分割机制限制了模型的表达能力，传统决策树算法通过形式为 \(x_i > k\) 的轴平行超平面对数据集进行划分，当真实边界不沿特征轴分布时，决策树往往需要构建复杂结构和密集决策边界，导致模型臃肿且可解释性下降。为克服传统决策树的局限性，斜决策树被提出作为改进方案。ODT 利用形式为 \(H(x)=h_{d+1}+\sum_{i=1}^{d}h_{i}x_{i}\) 的线性超平面进行分割，虽然能够生成更小更准确的树结构，但其斜分割规则涉及所有 d 个输入特征，使其更容易受到对抗性数据噪声的影响，同时可能降低模型的可解释性。

文章贡献

本文提出的 SREDT 模型融合了符号回归与决策树的优势，其核心思想是在决策树构建过程中，将传统的轴平行分割替换为通过符号回归发现的丰富数学表达式分割。SREDT 基于 CART 算法框架，但在每个节点分割时不再局限于单特征阈值比较，而是使用 GP 驱动的符号回归来探索特征间的复杂非线性关系，使 SREDT 能够发现那些需要多个传统分割才能近似表达的复杂决策边界。这种设计在保持决策树可解释性结构的同时，大幅提升模型的表达能力和效率。通过在 65 个数据集上的系统实验证明其在准确率、F1 分数和推理时间上均优于传统决策树和斜决策树，同时保持了高度可解释性。

本文方法

SREDT 基于 CART 算法，但将其分裂规则搜索过程替换为 SR 驱动的分裂。符号回归设置的函数集包括 \(\{ \text{add}, \text{mul}, \text{sub}, \text{div} \}\)，超参数诶：种群大小=400，迭代代数=40，锦标赛规模=200，简约系数=0.001。SREDT 的伪代码如下图所示，输入为当前节点数据集 \(N\)（含 \(D\) 个特征）和指定的分裂评价标准，如 Gini 不纯度。接着使用遗传编程（GP）生成候选表达式（如 \(X_0 \times X_1\)），并评估其分裂效果。然后对每个候选表达式寻找最佳分裂阈值（如 \(X_0 \times X_1 < 0.05\)），最后选择最优表达式和阈值作为节点分裂规则。

SR 传统上用于回归任务，SREDT 将其改造为分类器，即将 Gini 不纯度等分类指标作为 SR 的适应度函数。Gini 不纯度公式如下，其中 \(t\) 为当前节点，\(c\) 为类别数，\(n_{i,t}\) 为节点 \(t\) 中第 \(i\) 类样本数。

\[G(t) = 1 - \sum_{i=1}^{c} \left( \frac{n_{i,t}}{n_t} \right)^2 \]

分裂增益计算公式如下：

\[\Delta G = G(t) - \frac{n_f}{n_t} G(f) - \frac{n'_t}{n_t} G(t') \]

本文对 SREDT 设计了 3 种变体：

1. 预训练SREDT（P-SREDT）：使用 AI-Feynman 方程库预训练 RNN 生成初始种群，提升表达式质量。
2. 前瞻SREDT（L-SREDT）：引入单步前瞻机制，评估分裂对下一层树结构的影响。
3. 局部SREDT（Local SREDT）：在 SR 种群中增加局部搜索机制优化表达式中的常数项，损失函数使用可微的平方铰链损失：\(L(z) = (\max(0, -y \cdot \hat{z}))^2\)，其中 \(z\) 为样本值与阈值的差，\(y\) 为类别标签（±1）。使用 BFGS 算法优化常数，提升分裂边界的精确性。

实验结果

合成数据集实验

在合成数据集实验中，SREDT 展现出显著优势。XOR 分类问题中，传统决策树需要深度为 3 且包含 6 个叶子节点的结构，SREDT 仅通过深度为 1、2 个叶子节点的简洁树就解决了问题。

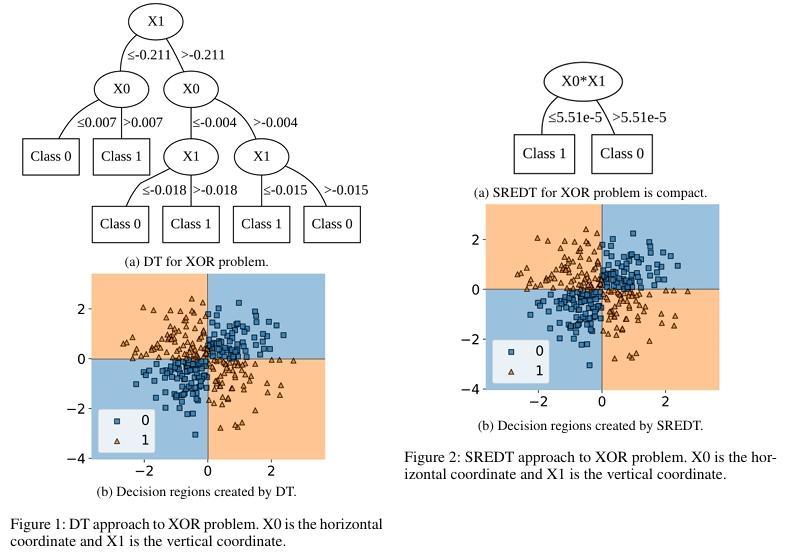
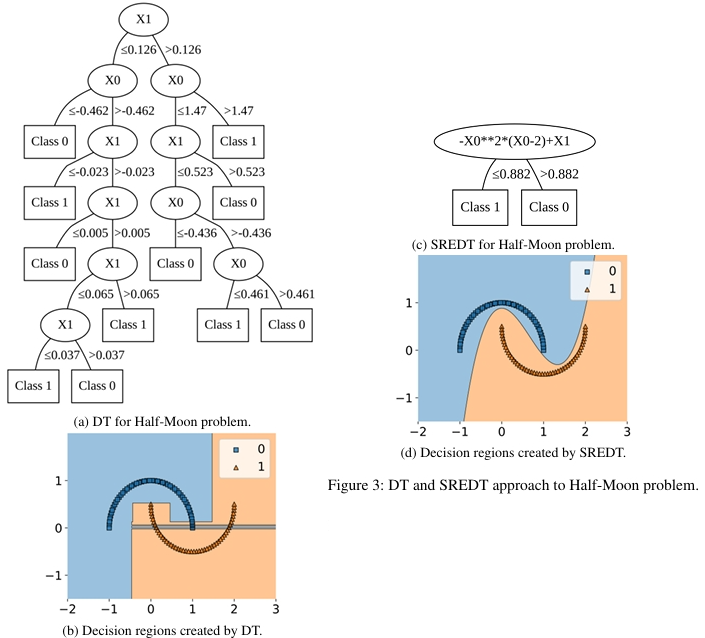
在半月亮分类问题中，决策树需要 11 个叶子节点和深度 6 才能完成的任务，SREDT 同样以单层结构解决。

真实数据集

在真实数据集中，SREDT 在准确率和 F1 两个关键指标上均超越了传统决策树和斜决策树。


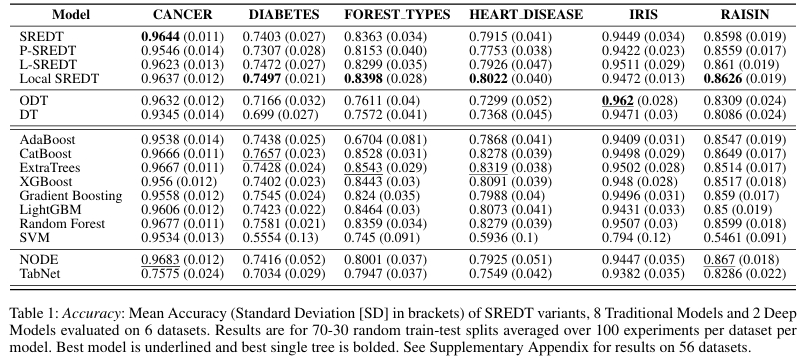
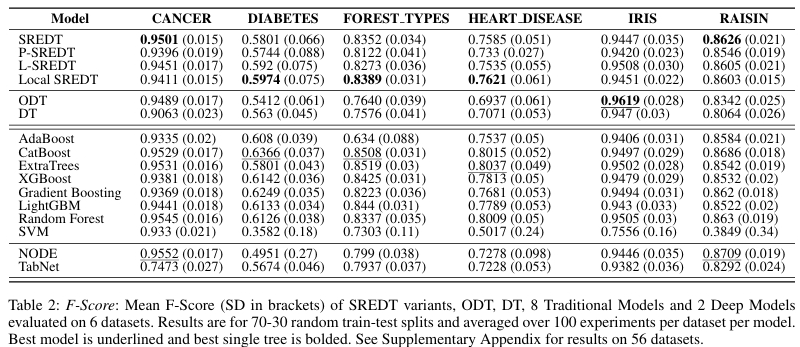
模型紧凑性分析显示，SREDT 在深度比率、叶子节点比率和项数比率方面都表现出更优的简洁性。

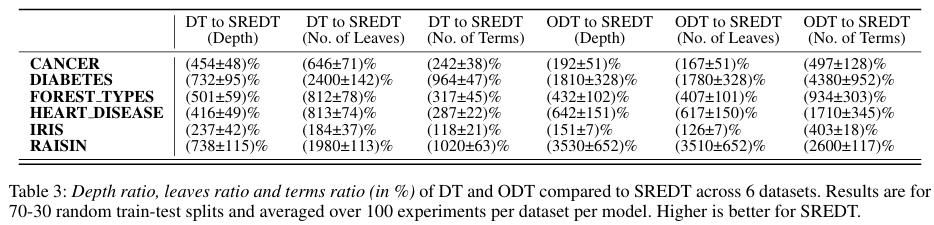
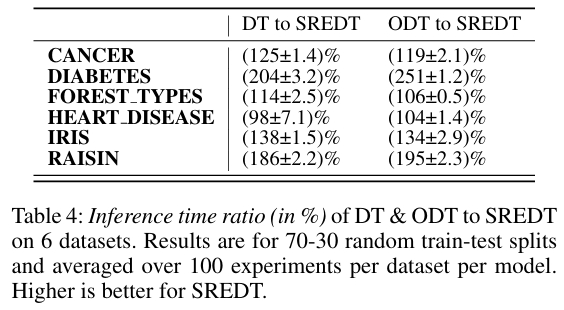
在推理时间方面，SREDT 比决策树减少 25.8% 的时间，比斜决策树减少 26.6%。SREDT 的训练时间较长，这是其探索更丰富分割空间所带来的必然代价。

噪声数据测试

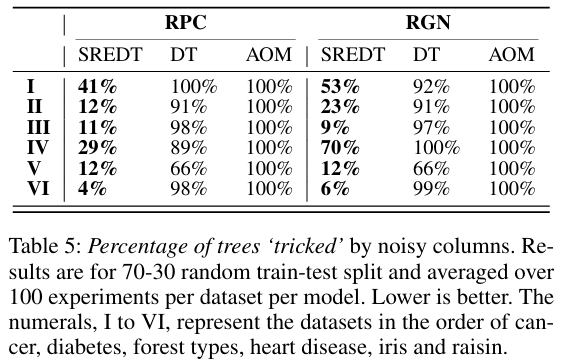
在对抗性数据噪声测试中，当引入随机排列列和随机高斯噪声时，SREDT 的准确率仅下降 1.7%、F1 分数下降 0.72%，表现出稳定性。

可解释分析

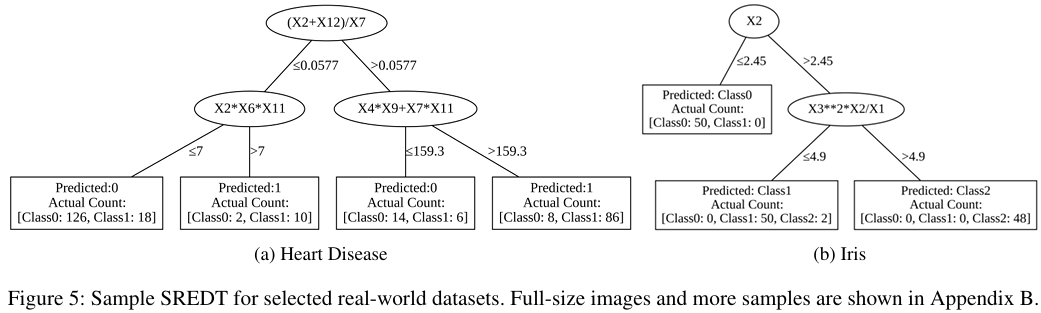
可解释性方面，SREDT 通过低深度、少叶子节点和少项数的设计，显著降低了用户的认知负荷。实际生成的决策树样本显示，SREDT 能够以人类可理解的形式呈现复杂的决策过程，这在需要模型解释的领域尤为重要。

优点和创新点

个人认为，本文通过遗传编程探索非线性分割规则，突破了传统决策树只能进行轴平行分割的局限性，在保持模型可解释性的同时显著提升了表达能力。SREDT 生成的树结构深度更浅、叶子节点更少，但在准确率和 F1 分数上超越传统决策树和斜决策树，实现了效率与效果的双重优化。