关于决策单调性的整理
1.决策单调性
在动态规划中,对于类似于 \(f_i=\min_{j=1}^{i-1} f_j+cost(j,i)\) 的转移方程,假设 \(p_i\) 表示 \(i\) 的最优决策点,\(\forall i\le j\) 均有 \(p_i\le p_j\),即称 \(f\) 具有决策单调性。
此时我们不妨假设 \(f\) 具有决策单调性,对于 \(i<j\),假设 \(p\) 为 \(i\) 的最优决策点,\(q\) 为 \(j\) 的最优决策点,那么当 \(q\in [1,i-1]\) 时,由决策点的最优性可以得到:
上下相加即有:
由于 \(f\) 的决策单调性,我们可以得到 \(p\le q\le i\le j\),由此,我们得到了四边形不等式的定义。
2.四边形不等式
四边形不等式:如果一个二元函数 \(w(x,y)\),对于 \(a\le b\le c\le d\) 均满足 \(w(a,c)+w(b,d)\le w(b,c)+w(a,d)\),那么称 \(w\) 满足四边形不等式。特殊的,如果 \(\forall a\le b\le c\le d\),\(w(a,c)+w(b,d) = w(b,c)+w(a,d)\) 恒成立,那么称 \(w\) 满足四边形恒等式,简单的记忆方法就是交叉小于包含。
至于为什么叫四边形不等式,看图:
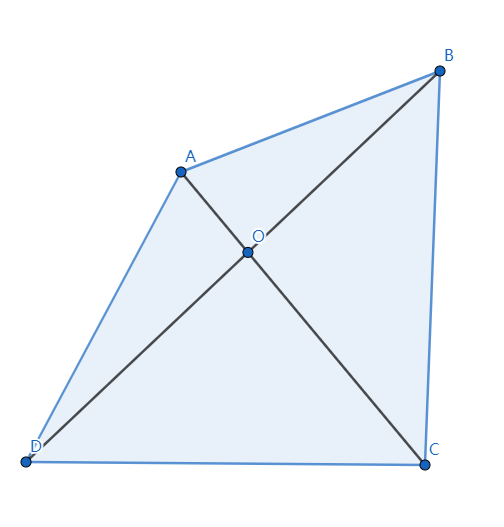
对于四边形 \(ABCD\),连接 \(AC\) 和 \(BD\),设 \(AC\ \cap\ BD=O\),定义函数 \(dis(x,y)\) 表示 \(x,y\) 两点之间的欧氏距离,那么根据三角形的边长关系,显然有
那么上下相加则有
也即
更改一下字母标号就可以得到四边形不等式的形式了。
3.四边形不等式的性质
性质 \(1\):对于任意整数 \(a,c\left(a<c\right)\) ,有 \(w(a,c)+w(a+1,c+1)\le w(a+1,c)+w(a,c+1)\) 恒成立,那么 \(w\) 满足四边形不等式。
证明:首先,对于任意整数 \(a,c\left(a<c\right)\),有这两条不等式成立
上下相加并整理即有 \(w(a,c)+w(a+1,c+2)\le w(a,c+2)+w(a+1,c)\) 成立,同理即可推得:\(w(a,c)+w(a+1,c+x)\le w(a,c+x)+w(a+1,c)\left(x\in[1,\infty)\right)\) 成立,也就是对于任意的 \(d\in [c+1,\infty)\),都有 \(w(a,c)+w(a+1,d)\le w(a,d)+w(a+1,c)\) 成立。
同理,对于 \(a<a+1<a+2\le c\),有两条不等式成立:
上下相加并整理即有 \(w(a,c)+w(a+2,d)\le w(a+2,c)+w(a,d)\) 成立,仿照上例即可推得对于任意的 \(b\in [a+1,c]\),都有 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)。
所以对于 \(a<b\le c<d\),都有 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\),而当 \(a=b\) 或 \(c=d\) 时,这个式子显然仍然成立,所以对于任意 \(a\le b\le c\le d\),都有 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\),也即 \(w\) 满足四边形不等式。
性质 \(2\):对于动态规划的转移方程 \(f_i=\min_{j=1}^{i-1}f_j+cost(j,i)\),如果 \(cost\) 满足四边形不等式,那么 \(f\) 具有决策单调性。
证明:假设 \(f\) 不具有决策单调性,假设 \(i\) 的最优决策点为 \(p_i\),且 \(p_i\) 是所有,那么一定 \(\exists i,j\) 使得 \(i<j\) 且 \(i>p_i>p_j\)。
由决策点的最优性,就有
上下相加并整理则有 \(cost(p_i,i)+cost(p_j,j)\le cost(p_j,i)+cost(p_i,j)\),又由于 \(cost\) 满足四边形不等式,因此有 \(cost(p_j,i)+cost(p_i,j)\le cost(p_j,j)+cost(p_i,i)\),所以 \(cost(p_i,i)+cost(p_j,j)=cost(p_j,i)+cost(p_i,j)\),又可以推得 \(f_{p_i}+cost(p_i,i)+f_{p_j}+cost(p_j,j)=f_{p_j}+cost(p_j+i)+f_{p_i}+cost_{p_i,j}\),也就是 \(f_{i}+f_j=f_{p_j}+cost(p_j+i)+f_{p_i}+cost_{p_i,j}\),又由 \(f_i\le f_{p_j}+cost(p_j,i)\),所以 \(f_j\ge f_{p_i}+cost(p_i,j)\),且 \(f_j\le f_{p_i}+cost(p_i,j)\),所以 \(f_j=f_{p_i}+cost(p_i,j)\),那么 \(j\) 的最优决策点选在 \(p_i\) 一定不劣,换句话说,\(p_j\) 必然可以等于 \(p_i\),这与 \(p_i>p_j\) 矛盾。
所以 \(f\) 不具有决策单调性不成立,也就是 \(f\) 具有决策单调性。
注意:\(cost\) 满足四边形不等式是 \(f\) 具有决策单调性的充分不必要条件,因为在利用 \(f\) 具有决策单调性的条件推出 \(cost\) 满足四边形不等式的过程中添加了 \(p_j\in [1,i-1]\) 这个条件,不然 \(f_{p_i}+cost(p_i,i)\le f_{p_j}+cost(p_j,i)\) 这条不等式是不成立的,也就无法推出 \(cost\) 满足四边形不等式的结论。
4.决策单调性优化 DP
1.从四边形不等式开始
在上文中已经说过,对于转移方程 \(f_{i}=\min_{j=1}^{i-1} f_j+cost(j,i)\),如果 \(cost\) 满足四边形不等式的话,对于任意两个决策点 \(i,j(i<j)\),设第一个使得 \(f_i+cost(i,x)>f_j+cost(j,x)\) 的 \(x\) 为 \(x_0\),那么对于 \(x\in [x_0+1,n]\),\(f_i+cost(i,x)>f_{j}+cost(j,x)\)。
证明:由于 \(f_i+cost(i,x_0)>f_j+cost(j,x_0)\) 且 \(cost\) 满足四边形不等式,可以得到
所以
所以
依次类推,可以推得对于 \(x\in [x_0,n]\),\(f_i+cost(i,x)>f_j+cost(j,x)\) 均成立。
这告诉我们,当 \(i\) 开始比 \(j\) 劣之后,就不会再比 \(j\) 优了,而 \(i\) 开始比 \(j\) 劣的时间可以通过二分在 \(O(\log n)\) 的时间复杂度内求得,记为 \(T(i,j)\)。
而对于三个决策点 \(i,j,k\left(i<j<k\right)\),如果 \(T(i,j)\ge T(j,k)\) 的话,说明在 \(j\) 比 \(i\) 优之前,\(k\) 就比 \(j\) 优了,所以 \(j\) 就绝对不会成为最优解了,那么就可以不考虑 \(j\) 这个决策点了,由此,我们就可以得到第一种决策单调性优化的方法,使用队列加决策单调性优化 DP。
2.队列加决策单调性优化 DP
1.优化方式
根据上面所说,我们可以使用一个双端队列来维护当前所有可能成为最优解的决策点,这就类似于单调队列维护当前可能成为最值的位置,所以我们同样需要进行入队和出队操作。
我们先来考虑入队操作,设位于队尾的位置为 \(y\),前一个位置为 \(x\),将要入队的元素为 \(z\),那么可以通过二分求出 \(T(x,y)\) 和 \(T(y,z)\),正如前面所说,如果 \(T(x,y)\ge T(y,z)\) 的话,说明 \(y\) 不可能成为最优解的决策点了,所以将 \(y\) 出队,重复操作直到队列中元素不足 \(2\) 个或者 \(T(x,y)<T(y,z)\) 时,将 \(z\) 入队。
然后考虑出队操作,不妨定义 \(cal(i,j)=f_j+cost(j,i)\),设位于队首的位置为 \(x\),后一个位置为 \(y\),如果 \(cal(i,x)>cal(i,y)\),说明此时 \(x\) 已经劣于 \(y\) 了,在之后也不可能优于 \(y\),则 \(x\) 不可能成为最优解,将 \(x\) 出队,直到找到当前的最优决策点,最后使用队首的决策点转移即可。
2.时间复杂度
考虑每个元素的操作的时间复杂度,类似于单调队列,每个元素只入队一次,出队一次,入队的时间复杂度是 \(O(1)\) 的,而出队时间复杂度分两种,如果在队首出队,那么也是 \(O(1)\) 的,在队尾出队的话,就是 \(O(\log n)\) 的,所以总时间复杂度是 \(O(n\log n)\) 的。
3.例题 [POI 2011]Lightning Conductor
题目要求对于每个 \(i\) 求出最小的 \(k\) 使得对于任意的 \(j\),\(h_i+k\ge h_j+\sqrt{|i-j|}\),那么 \(k=\max(h_j+\sqrt{|i-j|})-h_i\)。
尝试消去绝对值对答案的影响,那么就有 \(k+h_i=\max(\max_{j=1}^i(h_j+\sqrt{i-j}),\max_{j=i}^n(h_j+\sqrt{j-i}))\),那么只需要考虑怎么正着做,然后将这个序列翻转之后再做一次就可以了。
考虑到 \(f(x)=\sqrt x\) 这个函数的导函数 \(f^\prime(x)=\frac{1}{2\sqrt x}\) 是一个递减函数,所以我们可以猜测对于两个决策点 \(x,y\),如果 \(x<y\),那么当 \(x\) 比 \(y\) 劣之后将不会再比 \(y\) 优,那么尝试证明这个结论。
假设对于 \(i\),\(x\) 劣于 \(y\),而 \(\exists j,j>i\) 且 \(x\) 优于 \(y\),那么有
简单解这个不等式组即可得到 \(i\ge j\),与 \(i<j\) 矛盾,所以就可以使用队列解决策单调性来优化这个过程,这里给出范例实现。
const int N=5e5+5;
int n,tail,head;
int a[N],q[N];
double ans[N];
double cal(int i,int j){return a[j]+sqrt(i-j);
}
int find(int x,int y){ int l=y,r=n,res=n+1;while(l<=r){int mid=l+r>>1;if(cal(mid,x)<cal(mid,y)){res=mid;r=mid-1;}else l=mid+1;}return res;
}
bool check(int x,int y,int z){return find(x,y)>=find(y,z);
}
signed main(){read(n);for(int i=1;i<=n;i++)read(a[i]);tail=0,head=1;for(int i=1;i<=n;i++){while(head<tail&&check(q[tail-1],q[tail],i))tail--;q[++tail]=i;while(head<tail&&cal(i,q[head])<cal(i,q[head+1]))head++;if(head<tail)ans[i]=max(ans[i],cal(i,q[head]));}reverse(a+1,a+n+1);tail=0,head=1;for(int i=1;i<=n;i++){while(head<tail&&check(q[tail-1],q[tail],i))tail--;q[++tail]=i;while(head<tail&&cal(i,q[head])<cal(i,q[head+1]))head++;if(head<tail)ans[n-i+1]=max(ans[n-i+1],cal(i,q[head]));}reverse(a+1,a+n+1);for(int i=1;i<=n;i++)write(ceil(max(ans[i]-a[i],0.0))),Nxt;
}
3.分治加决策单调性优化 DP
1.为什么要使用分治加决策单调性优化 DP?
上面所述的队列加决策单调性优化 DP 只适用于函数满足四边形不等式的情况,否则对于决策点 \(x,y\),可能出现优劣性反复横跳的情况,比如对于下面的函数图:
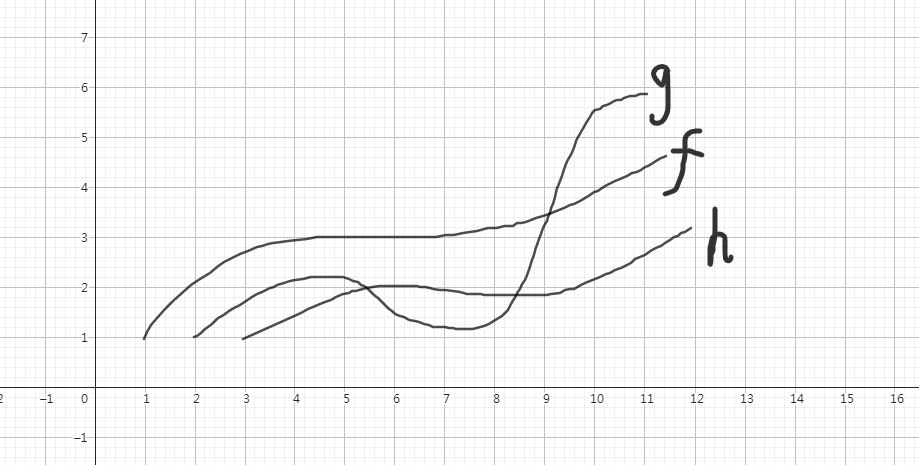
函数 \(f,g,h\) 分别表示决策点 \(1,2,3\) 的贡献的变化,显然这也是符合决策单调性的,但是决策点 \(2\) 刚开始比 \(3\) 优,紧接着又比 \(3\) 劣,但是最后又变成了最优决策点,显然不能用队列来优化了,我们需要一种其他的方式来进行优化,使用分治加决策单调性优化 DP 也就应运而生(虽然实际题目中很难出现这种牛鬼蛇神的贡献函数,但是这种方法它也更好写呀!)。
2.优化方式
我们在分治时记录当前所有需要计算的转移点可能的最优决策点的区间,可以想见,这是一个连续的区间,所以分治的参数也就是 \(l,r,L,R\),表示当前需要计算的转移点为 \([l,r]\),可能的最优决策点的区间为 \([L,R]\)。
首先,找到需要计算的转移点的中点 \(mid\),然后用 \([L,R]\) 中所有可以转移到 \(mid\) 的决策点暴力尝试转移,找到最优决策点的位置 \(p\),那么根据决策单调性,对于 \([l,mid-1]\) 的所有转移点,最优决策点只可能在 \([L,p]\) 区间内出现,对于 \([mid+1,r]\) 的所有转移点,最优决策点只可能在 \([p,R]\) 区间内出现,递归解决这个问题即可。
3.时间复杂度
考虑每个决策点被计算几次,在每一层,一个决策点最多只会被计算两次,这些决策点就是上一层的最优决策点,而一共只有 \(\log n\) 层,所以时间复杂度为 \(O(V\log n)\),其中 \(V\) 表示决策点的数量,在实际题目中一般就是 \(n\),因此时间复杂度也可视为为 \(O(n\log n)\)。
4.例题 [SDOI2016] 征途
首先推式子,假设 \(dis_i\) 表示第 \(i\) 天走的路程,那么最后得到的方差就是 \(\frac{1}{m}\sum_{i=1}^m(dis_i-\overline{dis})^2\)。
很显然,\(\overline{dis}=\frac{len}{m}\),其中 \(len\) 表示 总路程,因此带入并展开计算的公式就可以得到方差等于
进而得到方差等于
而显然,\(\sum_{i=1}^m dis_i=len\),所以方差等于
又因为最后得到的结果需要乘 \(m^2\),所以得到的结果就是
需要最后的结果最小,就只需要使每一天走的路程的平方和最小即可,那么就可以使用动态规划计算。
定义状态 \(f_{i,j}\) 表示将 \([1,j]\) 的路程分成 \(i\) 天走完的平方和的最小值,那么转移也是显然的:\(f_{i,j}=\min_{k=i-1}^{j-1} \{f_{i-1,k}+(pre_j-pre_k)^2\}\) ,暴力 DP 的时间复杂度为 \(O(n^2m)\),需要优化。
由于函数 \(f(x)=x^2\) 的导函数 \(f^\prime(x)=2x\) 是一个递增函数,所以 \(f\) 可能具有决策单调性,故尝试证明,假定 \((k,i)\) 的最优决策点为 \(p\),\((k,j)\) 的最优决策点为 \(q\),满足 \(i<j\) 且 \(p>q\),那么由决策点的最优性可以得到
也就是
那么 \(pre_ipre_p+pre_jpre_q\ge pre_ipre_q+pre_jpre_p\),也就是 \(pre_i(pre_p-pre_q)\ge pre_j(pre_p-pre_q)\),由于 \(i<j\),所以 \(pre_i<pre_j\),所以 \(pre_p-pre_q\le 0\),也就是 \(p\le q\),与 \(p>q\) 矛盾,因此 \(f\) 存在决策单调性,那么可以使用分治加决策单调性对这个 DP 进行优化,时间复杂度为 \(O(mn\log n)\)。(当然价值函数也是满足四边形不等式的,所以这里用队列加决策单调性优化也可以,不过为了演示分治的写法,这里使用分治加决策单调性优化)
const int N=3005;
int n,m;
int a[N],pre[N],f[N][N];
int cal(int l,int r){return (pre[r]-pre[l-1])*(pre[r]-pre[l-1]);
}
void CDQ(int idx,int l,int r,int L,int R){//CDQ 已经从一个人名演变为分治的代名词了(大雾)if(l>r)return ;int mid=l+r>>1,p;for(int i=L;i<=min(mid-1,R);i++){if(f[idx][mid]>f[idx-1][i]+cal(i+1,mid)){f[idx][mid]=f[idx-1][i]+cal(i+1,mid);p=i;}}CDQ(idx,l,mid-1,L,p);CDQ(idx,mid+1,r,p,R);
}
signed main(){read(n),read(m);for(int i=1;i<=n;i++)pre[i]=pre[i-1]+read(a[i]);memset(f,0x3f,sizeof(f));for(int i=1;i<=n;i++)f[1][i]=cal(1,i);for(int i=2;i<=m;i++)CDQ(i,i,n,i-1,n-1);write(m*f[m][n]-pre[n]*pre[n]);
}
5.算法局限性
别看这个分治加决策单调性优化 DP 这么好写,但这写法也是有局限的,这种写法一般只能应用于分阶段的 DP,比如将序列分成要求的段数,这样从上一阶段转移到下一阶段,在同一阶段中 \(f\) 的计算顺序不受限制,否则我们需要先求出 \(f_{i-1}\),然后才能正确的求出 \(f_i\),这样的写法也就失去了正确性,此时就需要分治套分治来保证 \(f\) 的计算顺序,时间复杂度变为 \(O(n\log ^2n)\),同样考虑计算一个决策点计算几次,对于一个决策点 \(x\),它会出现在第二次分治的第一层 \(\log n\) 次,而同样的,它每一次出现在第二次分治中会被计算 \(n\log n\) 次,所以时间复杂度为 \(O(n\log^2n)\)。
4.斜率优化
决策单调性还有一类特殊的优化方式,当满足一些条件的时候可以将转移优化到 \(O(n)\),这种优化方式由于使用了解析几何中的一次函数与斜率这两个概念,被称为斜率优化。
1.从凸包说起
什么是凸包?简单的说,对于一个平面上的若干点,可以完全包括这些点的最小的凸多边形称为凸包,形象地描述就是在地上插一堆木桩子,然后使用一条足够大的橡皮筋把这些木桩子全部围起来,最后橡皮筋的形状就是这些点组成的凸包,如下图所示,就是一个凸包:
那么怎么维护凸包呢?由于在斜率优化中我们一般不建出整个凸包,而只维护凸壳(凸壳就是一个凸包的一部分,上凸壳就是凸包的上半部分,下凸壳就是凸包的下半部分),因此我们这里可以使用维护上/下凸壳的 Andrew 算法,这种算法理解起来更简单,实现起来也比较简短。
首先,将所有点按照 \(x\) 坐标排序,那么第一个点(也就是 \(x\) 坐标最小的点)一定在凸包中,将其放入一个栈中,然后依次枚举所有点,而当前点是已经考虑的点集中 \(x\) 坐标最大的点,也一定在凸包中,因此我们尝试将这个点加入凸包中,并且删除不合法的点。
如何判断一个点是否合法?这里以下凸壳为例,很显然有结论,下凸壳的每条边的斜率递增。那么假定当前栈顶的点为 \(A(x_1,y_1)\),次栈顶的点为 \(B(x_2,y_2)\),而将要入栈的点为 \(C(x_3,x_4)\),而由于斜率递增,所以当 \(K_{BA}\ge K_{AC}\) 时,说明 \(A\) 点不在凸包中,将 \(A\) 弹出即可。重复操作直到 \(K_{BA}<K_{AC}\) 或栈中只剩一个点为止,将当前点加入栈中。
2.优化方式
形如转移方程 \(f_i=\min(f_j+cost(j,i))\),如果 \(cost(j,i)=c_1(j)+c_2(i)\),其中 \(c_1(j)\) 和 \(c_2(i)\) 分别是关于 \(j,i\) 的一元函数,那么可以使用单调队列将时间复杂度优化到 \(O(n)\),但是如果 \(cost(j,i)=c_1(j)+c_2(i)+c_3(j,i)\),其中 \(c_3(j,i)\) 是关于 \(j,i\) 的二元二次函数,那么单纯的使用单调队列优化就无法实现了,此时需要使用斜率优化。
不妨假定转移方程为 \(f_i=\min(f_j+c_1(j)+c_2(i)+c_3(i)c_4(j))\),其中 \(c_1(j),c_2(i),c_3(i),c_4(j)\) 都是关于 \(j,i\) 的一元函数,那么直接考虑最优转移点 \(p\) 的情况 \(f_i=f_p+c_1(p)+c_2(i)+c_3(i)c_4(p)\),可以得到 \(-f_p-c_1(p)=c_3(i)c_4(p)+c_2(i)-f_i\),此时我们设 \(x_p=c_4(p),y_p=-f_p-c_1(p),k=c_3(i),b=c_2(i)-f_i\),也就得到 \(y_p=kx_p+b\),这是一条我们熟悉的一次函数的表达式,而我们需要求解 \(f_i\),也就是求解 \(b\),这就相当于求过一个已知点的斜率已知的直线的截距,可以想见,最优转移点一定在下凸壳上,并且最优的那条直线一定是下凸壳的切线,所以我们只需要维护下凸壳并求解下凸壳的切线即可。
3.队列维护凸壳
当题中所给的 \(x\) 递增,我们可以顺序加入所有决策点,而如果同时 \(k\) 也递增的话,切点只会不断右移,这是显然的,所以我们就可以用队列维护凸壳,然后在队首维护切点,维护切点的方式类似于队列加决策单调性优化 DP 时的队首出队操作,判断对当前转移点,队首决策点和次队首决策点哪个更优,如果队首不优则出队,最后直接使用队首的点进行转移即可,显然每个点只入队一次,出队一次,时间复杂度为 \(O(n)\)。
例题 [USACO08MAR] Land Acquisition G
首先所有被包含的土地肯定与包含它的土地绑定购买,因此考虑将所有土地按照 \(h\) 为第一关键字,\(w\) 为第二关键字排序,那么所有不被包含的土地的 \(h\) 肯定构成一个递增序列,\(w\) 构成一个递减序列,由此处理出所有不被包含的土地。
然后我们一定购买一段连续的土地,这样对答案有贡献的只有最右边一块土地的 \(h\) 和最左边一块土地的 \(w\),所以我们定义 \(f_i\) 表示购买了前 \(i\) 块土地的最低价格,那么 \(f_i=\min_{j=0}^{i-1}f_j+w_{j+1}\times h_i\),暴力转移的时间复杂度为 \(O(n^2)\),显然需要优化。
考虑转移方程符合斜率优化的形式,因此直接对式子进行变形得到 \(-f_j=h_iw_{j+1}-f_i\),两边取反则有 \(f_j=-h_iw_{j+1}+f_i\),由此就有 \(y_j=f_j,x_j=-w_{j+1}\) 了,显然有 \(x\) 坐标递增,直接丢入维护下凸包即可,而斜率 \(k=h_i\) 也是递增的,于是可以使用队列维护凸壳来优化转移,时间复杂度为 \(O(n\log n)\),瓶颈在于排序。
const int N=50005;
int n,m,head,tail;
int x[N],y[N],q[N],dp[N];
bool mark[N];
struct Node{int h,w;bool operator <(const Node &a)const{if(h!=a.h)return h<a.h;return w<a.w;}
}a[N];
bool check(int s,int mid,int t){return (y[mid]-y[s])*(x[t]-x[mid])>=(y[t]-y[mid])*(x[mid]-x[s]);
}
int cal(int i,int j){return y[j]-a[i].h*x[j];
}
signed main(){read(n);for(int i=1;i<=n;i++)read(a[i].h),read(a[i].w);sort(a+1,a+n+1);for(int i=n,mx=-1;i>=1;i--){if(mx<a[i].w){mark[i]=1;mx=a[i].w;}}for(int i=1;i<=n;i++)if(mark[i])a[++m]=a[i];n=m;head=1,tail=0;for(int i=1;i<=n;i++){x[i-1]=-a[i].w,y[i-1]=dp[i-1];while(tail>head&&check(q[tail-1],q[tail],i-1))tail--;q[++tail]=i-1;while(tail>head&&cal(i,q[head])>cal(i,q[head+1]))head++;dp[i]=cal(i,q[head]);}write(dp[n]);
}
4.栈维护凸壳
然鹅,并不是每一道的转移方程都是这么友善的让你的 \(x\) 坐标与斜率 \(k\) 都递增的,有些题目就不满足 \(k\) 递增的条件,此时切点就不递增了,因此我们不能简单地直接从队首弹出元素,而是应该使用一个栈维护整个凸包,并在凸包上二分切点来保证转移正确性,除了最后求解的过程和队列维护凸壳稍有不同,其余和队列维护凸壳都是一样的。
就以上一题为例,其他部分都是相同的,最后在求解的时候可以这样二分:
int l=1,r=top;
while(l<r){int mid=l+r>>1;if(cal(i,st[mid])>cal(i,st[mid+1]))l=mid+1;else r=mid;
}
f[i]=cal(i,st[l]);
其中 \(cal(i,j)\) 表示从 \(j\) 转移到 \(i\) 的 dp 值。
5.分治维护凸壳
然鹅,还有些抽象题目,它连 \(x\) 坐标递增都不满足……这个时候就需要请出分治来维护凸壳了!
首先我们把所有点按 \(x\) 坐标排一手序,如果 \(x\) 坐标相同就比 \(y\) 坐标,记得这里要记录原下标!然后递归。
假设现在分治到了区间 \([l,r]\),设 \(mid=\frac{l+r}{2}\),然后把当前区间中原下标小于等于 \(mid\) 的点和大于\(mid\) 的点分开,由于 \([mid+1,r]\) 并不能更新 \([l,mid]\),因此我们可以先递归求出 \([l,mid]\) 的值,然后将 \([l,mid]\) 的所有点维护成一个凸壳去更新 \([mid+1,r]\),然后继续递归计算 \([mid+1,r]\)。
时间复杂度显然为 \(O(n\log n)\)。
例题 [CEOI 2017] Building Bridges,代码鸽了。



















