P5322 [BJOI2019] 排兵布阵
我们可以预处理出第 \(i\) 个城堡分配 \(j\) 的兵力能获得多少的得分,记为 \(w[i][j]\)。
则每一个 \(w[i]\) 都是一个泛化物品,即价值(\(w[i][j]\))随着分配体积(\(j\))变化的物品。将两个泛化物品合并的代价是 \(O(m^2)\) 的,总时间 \(O(nm^2)\) 无法接受。
但是我们将问题过度一般化了。实际上这个泛化物品只有 \(s\) 个分段点,完全可以看作一个 \(s\) 个物品的分组背包。若按体积(兵力)为这些物品排序,它们的价值实际上相当于求了原序列的一个前缀和,即 \(i,2i,3i,\dots\)。
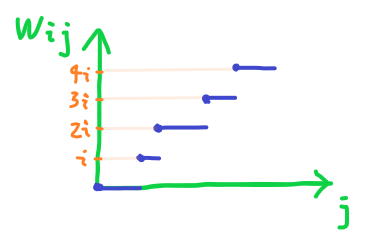
所以分组背包即可。时间复杂度 \(O(nms)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=102,M=20002,S=102;
int s,n,m,a[N][S],f[M];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>n>>m;for(int i=1;i<=s;i++) for(int j=1;j<=n;j++) cin>>a[j][i];for(int i=1;i<=n;i++) sort(a[i]+1,a[i]+1+s);for(int i=1;i<=n;i++){for(int k=m;k;k--){for(int j=1;j<=s;j++){if(k>2*a[i][j]) f[k]=max(f[k],f[k-2*a[i][j]-1]+i*j);}}}cout<<f[m]<<"\n";return 0;
}
学到的:分组物品,对于每一组,若某个物品体积 \(\le\) 该组分配的体积即可选(即取 \(\max\) 而非求和),则可以通过对价值前缀和而转为分组背包。

附安装包)



)


![Luogu P7913 [CSP-S 2021] 廊桥分配 题解 [ 绿 ] [ 贪心 ] [ 前缀和 ] [ STL ]](http://pic.xiahunao.cn/Luogu P7913 [CSP-S 2021] 廊桥分配 题解 [ 绿 ] [ 贪心 ] [ 前缀和 ] [ STL ])










