10-27 CSP 赛前比赛记录

DNA 序列（DNA）

哈希题啊，但是忘了怎么写哈希了 qwq，所以……

思路大概就是维护一个长度为 \(k\) 的四进制数，类似于一个滑动窗口，就是除以 \(4\) 后加上右边新加的数乘上 \(4^k\)，就可以得到其对应的哈希值，取模嘛……就需要逆元了，所以就自然溢出了（不是，自然溢出带除法也不太对吧……），然后统计出现次数最多的就过了。

小奇采药(medicine)

0-1 背包板子？但是背包容量 \(\le 10^9\)，所以这道题是玄学。

咳咳，对于这道题目，我们只能搜索，由于数据随机，所以……启发式搜索神力！

直接 A* 就干完了。

估价函数长这样：

inline long long f(long long t, long long v) {long long h = 0;for (int i = t + 1 ; i <= n ; i++) {if (v >= a[i].c){v -= a[i].c;h += a[i].v;}else return (long long)(h + v * a[i].cost);}return h;
}

脑洞治疗仪 (brainhole)

区间合并线段树裸题啊……

本题要求维护最长连续 \(0\)，但和最大子段和类似。

维护最大子段和：

1、最大子段和合并：

有三种情况，如图：

对这三种情况取最大值就是合并后的最大子段和，查询时的合并是将最大后缀和合并，分类讨论判断是否需要同 LCA 一同合并，如果需要，可将两个最大后缀和与 \(0\) 取最大值，因为 LCA 可以选择不之合并。

2、区间和合并：
直接将两个区间和相加即可。

3、最大前缀和合并：
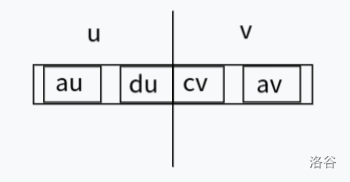
有两种情况，第一种最大前缀和就是 \(c_u\)，第二种是 \(b_u+c_v\)，然后对两种情况取最大值。

4、最大后缀和合并：
同最大前缀和合并一样，有两种情况，第一种是 \(d_v\)，第二种是 \(b_v+d_u\)，对两种情况取最大值即可。

综上可以得出：
\(a_f=\max(c_v+d_u,a_u,a_v),b_f=b_u+b_v,c_f=\max(c_u,b_u+c_v),d_f=\max(d_v,b_v+d_u)\)。

然后我们在分别维护区间 \(0\) 的数量，就可以得到区间长度。

在合并是特判区间长度是否等于前后缀最大值，就可以得到最大连续长度。

然后维护区间赋值、区间求和、区间最长连续 \(0\) 即可

至于填补，线段树上二分找到操作边界进行赋值即可。

然后就干完了。