剑指offer-35、数组中的逆序对

题⽬描述

在数组中的两个数字，如果前⾯⼀个数字⼤于后⾯的数字，则这两个数字组成⼀个逆序对。输⼊⼀个数组，求出这个数组中的逆序对的总数。

输⼊⼀个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

示例 1:
输⼊: [7,5,6,4]
输出: 5
限制：0 <= 数组⻓度 <= 50000

思路及解答

暴⼒破解

⾸先，也就是数组中任意两个数，只要前⾯的数⼤于后⾯的数，就是逆序对。先来⼀次暴⼒破解：遍历任意两个数，只要符合条件，总数就增加1。

class Solution {public int reversePairs(int[] nums) {int i=0, j=0, sum=0;for( i=0; i<nums.length; i++ ){for( j=i+1; j<nums.length; j++ ){if( nums[j] < nums[i] ) sum++;}}return sum;}
}

• 时间复杂度​：O(n²) - 对于每个元素，都需要与后续所有元素比较
• ​空间复杂度​：O(1) - 只使用常数级别额外空间

归并排序法（推荐）

在归并排序的基础上稍微改动即可。以数组[8,6,4,2,7,5,3,1]为例：

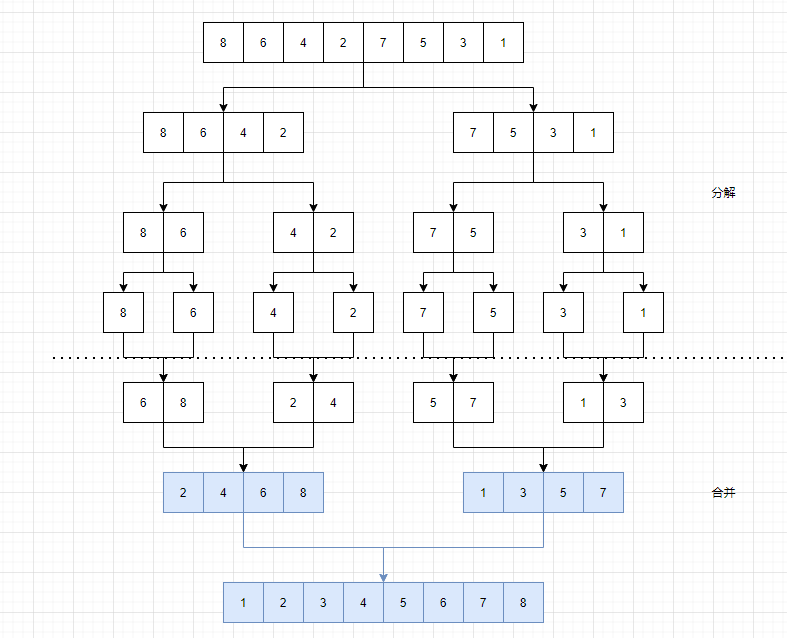
我们可以发现，其实在合并的过程中，两个有序的数组，可以直接计算出逆序数组的个数。我们以[8,6,4,2,7,5,3,1] ，实际上分为 [8,6,4,2] 和 [7,5,3,1] ，逆序的个数为第⼀部分 [8,6,4,2] 中的逆序个数+第⼆部分 [7,5,3,1] 中的逆序个数，还有第三部分是 [8,6,4,2] 中的元素相对 [7,5,3,1] 的逆序个数。

分为两半之后的逆序个数，⼀看就是分治法，递归即可，⽽两部分的相对逆序，我们可以在合并有序数组的时候得出。

合并的时候使⽤双指针， i 指向第⼀个数组的第⼀个元素，j指向第⼆个数组的第⼀个元素。哪⼀个元素⼩，就将该元素写⼊新的数组中，同时指针后移。

如果第⼆个数组中的元素⼩于第⼀个数组中的元素，那么就构成了逆序对，逆序对的个数：如果中间分隔是索引是 mid ，那么构成逆序对的个数为 mid-i+1 。

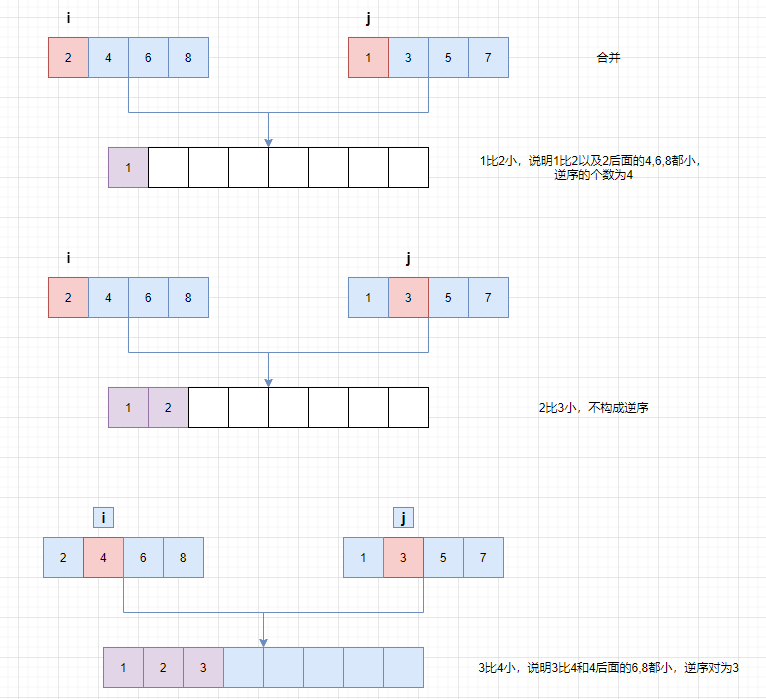
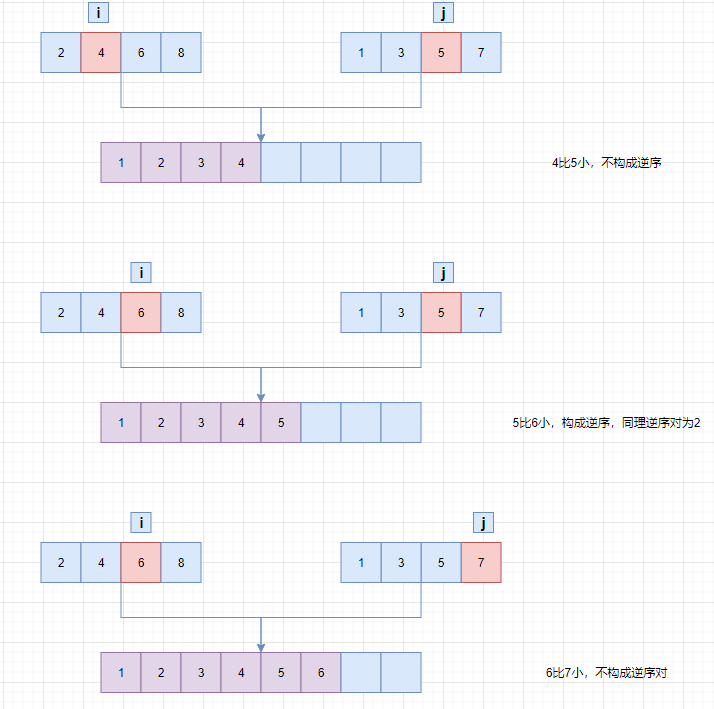
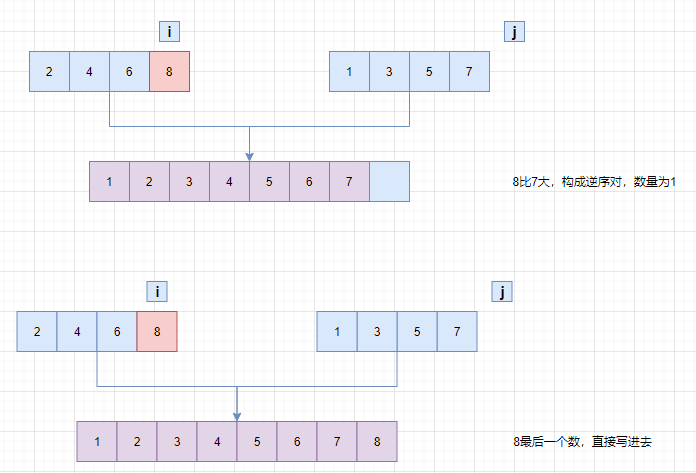
核心原理：​​当左子数组的当前元素 temp[i]大于右子数组的当前元素 temp[j]时，左子数组中从 i到 mid的所有元素都与 temp[j]构成逆序对，因为左右子数组都是有序的

public class Solution35 {public static void main(String[] args) {int[] nums = {8, 6, 4, 2, 7, 5, 3, 1};Solution35 solution35 = new Solution35();int result = solution35.InversePairs(nums);System.out.println(result);}public int InversePairs(int[] array) {if (array == null || array.length < 2) {return 0;}int[] nums = new int[array.length];return getNums(array, nums, 0, array.length - 1) % 1000000007;}public int getNums(int[] array, int[] nums, int left, int right) {if (left >= right) {return 0;}int mid = left + (right - left) / 2;int leftNum = getNums(array, nums, left, mid) % 1000000007;int rightNum = getNums(array, nums, mid + 1, right) % 1000000007;return leftNum + rightNum + mergeNum(array, nums, left, mid, right);}public int mergeNum(int[] array, int[] nums, int left, int mid, int right) {for (int i = left; i <= right; i++) {nums[i] = array[i];}int count = 0;int i = left, j = mid + 1;for (int k = left; k <= right; k++) {if (i == mid + 1) {array[k] = nums[j];j++;} else if (j == right + 1) {array[k] = nums[i];i++;} else if (nums[i] <= nums[j]) {array[k] = nums[i];i++;} else {array[k] = nums[j];j++;count = (count + (mid - i + 1)) % 1000000007;}}return count % 1000000007;}
}

• 时间复杂度​：O(n log n) - 与归并排序相同
• ​空间复杂度​：O(n) - 需要临时数组存储

有⼀个很坑的地⽅：只要涉及到加和的地⽅都有可能溢出，⼀旦溢出就会导致结果出错，数据量⼤，很难调试。所以凡是涉及到加和的地⽅都要 % 1000000007 。

树状数组法

利用树状数组（Fenwick Tree）和离散化技术统计逆序对

import java.util.*;public class Solution {private int mod = 1000000007;public int InversePairs(int[] nums) {if (nums == null || nums.length == 0) return 0;// 离散化处理：将原数组映射到紧凑的整数范围int[] sorted = nums.clone();Arrays.sort(sorted);// 创建映射：原数组值 -> 离散化后的索引（从1开始）Map<Integer, Integer> mapping = new HashMap<>();int index = 1;for (int num : sorted) {if (!mapping.containsKey(num)) {mapping.put(num, index++);}}// 使用树状数组统计逆序对FenwickTree tree = new FenwickTree(index - 1);int count = 0;// 从右向左遍历，统计每个元素左边比它小的元素数量for (int i = nums.length - 1; i >= 0; i--) {int pos = mapping.get(nums[i]);count = (count + tree.query(pos - 1)) % mod; // 查询比当前元素小的数量tree.update(pos, 1); // 更新树状数组}return count;}// 树状数组实现class FenwickTree {private int[] tree;private int n;public FenwickTree(int size) {this.n = size;this.tree = new int[size + 1];}// 低位操作private int lowBit(int x) {return x & (-x);}// 更新操作：在位置x增加valuepublic void update(int x, int value) {while (x <= n) {tree[x] = (tree[x] + value) % mod;x += lowBit(x);}}// 查询操作：求前x项的和public int query(int x) {int sum = 0;while (x > 0) {sum = (sum + tree[x]) % mod;x -= lowBit(x);}return sum;}}
}

• 间复杂度​：O(n log n) - 离散化O(n log n)，树状数组操作O(log n)
• ​空间复杂度​：O(n) - 树状数组和映射表空间