使用迭代优化递归程

封面：从斐波那契数列到递归.png

王有志，一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群：共同富裕的Java人

今天我们将会分析上篇文章中递归算法存在的问题，并通过迭代去优化。

递归存在的问题

上一篇中，我们计算了序号10以内的斐波那契数。今天为了清晰的展示递归解法存在的问题，我们试着计算序号为50的斐波那契数，如果电脑的性能较差的话，就不要尝试了。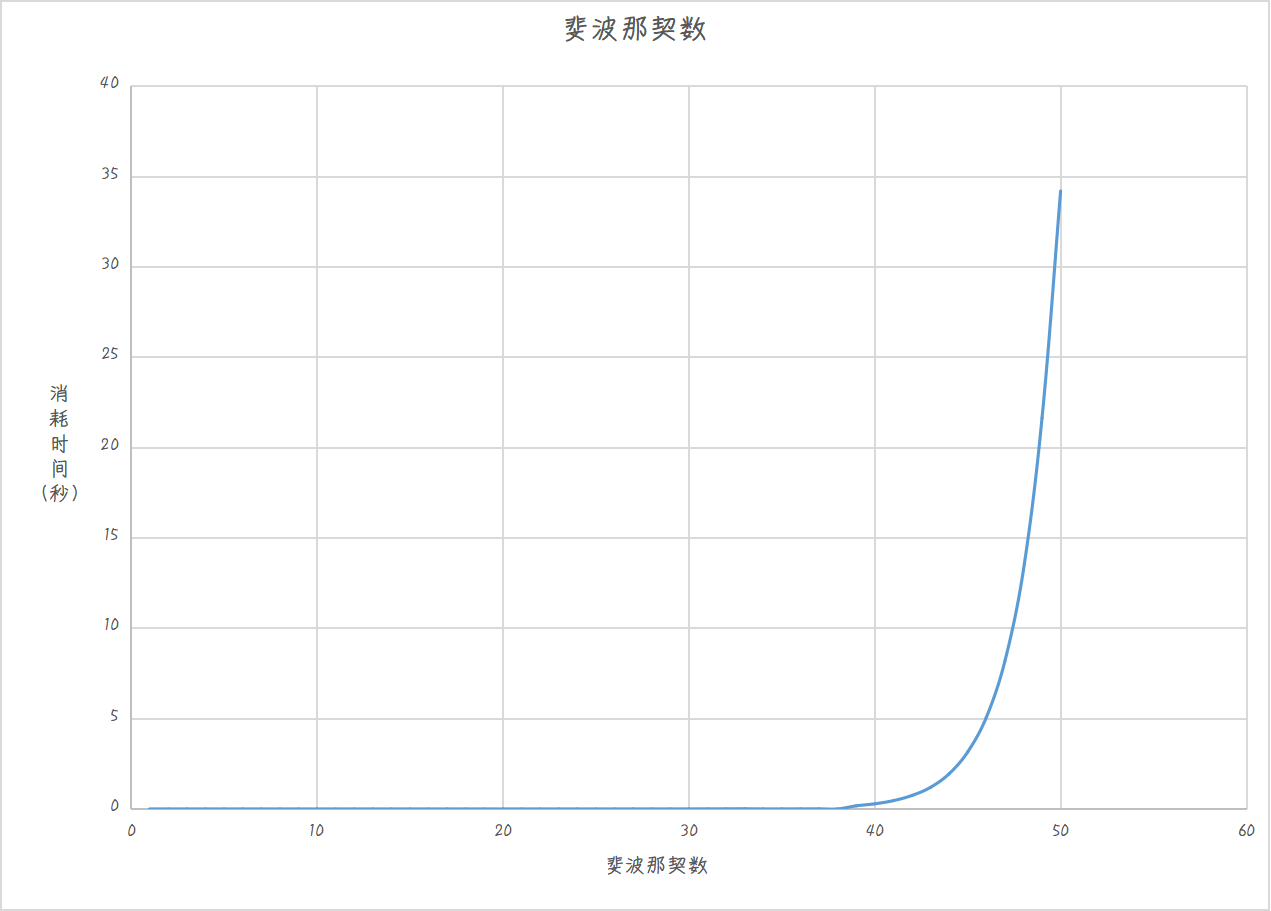
图1：斐波那契数列执行时间.png
可以看到，从计算F(40)开始，递归解法的耗时如同“坐火箭”般上升，这种情况是我们无法忍受的。
在上一篇文章中，我们有一个练习就是优化递归求解第n个斐波那契数。那么今天，我们就一起看看通过递归求解，问题出现在哪里？
通过之前构建的F(6)的递归树，我们可以看到，递归求解斐波那契数时，存在大量重复的计算，例如：仅仅是计算F(2)就出现了5次。
那么比较容易想到的优化方案就是缓存计算结果，使用时再取出。因此我们引入缓存，减少重复计算，提升执行速度（和复杂度分析中的空间换时间呼应上了）。
我们来看下具体实现：

private static long fib_recursion_memory(int n) {
return fib_recursion_memory(n, new long[n + 1]);
}private static long fib_recursion_memory(int n, long[] memory) {if (n < 2) {return n;}if (memory[n] != 0) {return memory[n];}memory[n] = fib_recursion_memory(n - 1, memory) + fib_recursion_memory(n - 2, memory);return memory[n];
}

代码并不复杂，通过引入long类型数组，记录已经计算过的斐波那契数，以达到减少重复计算的目的。
除此之外，还有没有其他方法求解第n个斐波那契数？

迭代

我们在使用递归时，通常是将规模较大的问题拆分为规模较小的问题，依次求解组合的过程。反之我们也可以从最小规模的问题开始，逐步累积到规模较大的问题。
迭代正是这样一种方法。迭代是数学概念引入编程中的，非常容易与循环混淆。来看下百度百科中的定义：

迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

既然说到非常容易与循环混淆，那么再来看看循环的定义：

循环是程序设计语言中反复执行某些代码的一种计算机处理过程，常见的有按照次数循环和按照条件循环。

通过定义我们很容易看出迭代与循环的差别，循环只是程序的重复执行，对计算结果没有要求，而迭代需要将每次计算结果应用到下一次循环中，所以可以说迭代只循环的子集。

迭代求解第n个斐波那契数

事实上，递归都是可以改写为迭代的形式（不那么优雅），而且邓俊峰老师也在《数据结构》中说到：

实际上，属于尾递归形式的算法，均可以简捷地转换为等效的迭代版本。

这给了我们使用迭代改写递归求解斐波那契数列的理论基础，下面我们直接开始。
首先斐波那契数列的的递推公式是从第3项开始，因此我们需要处理第1，2项的特殊情况，代码如下：

if(n <= 0) {return 0
}if(n < 3) {return 1;
}

根据递推公式，如果计算n的值，我们需要知道 n−1 和 n−2 的值，那么我们声明3个变量，用p代表 n−2 ，用q代表 n−1 ，用result代表n，那么p设置为 F(1) ，q设置为 F(2) ，result设置为 F(3) ，代码如下：

int p = 1, q = 1, result = p + q;

现在我们已经有了3个变量，表示 F(1) 到 F(3) ，仅仅是这些，你已经可以计算出F(4)的值了：

p = q;
q = result;
result = p + q;

如果想要计算 F(n) 的值，我们只需要不断的重复计算 F(4) 的过程即可：

for(int i = 4; i <= n; i++) {p = q;q = result;result = p + q;
}

完整的代码如下：

private static int fib(int n) {
if(n <= 0) {return 0;
}if (n < 3) {return 1;
}int p = 1, q = 1, result = p + q;
for (int i = 4; i <= n; i++) {p = q;q = result;result = p + q;
}
return result;
}

随着循环的进行，每次计算的结果都会带入到下一次的循环，这就是定义中所指的每次迭代结果作为下一次迭代的初始值进行处理。
至于通过迭代求解的斐波那契数列的时间复杂度，相信大家一眼就可以看出来了吧？
如果你了解动态规划的话，你很容易就能想到，迭代求解斐波那契数列就是简单的动态规划解法，不过这是后话，现在我们按下不表。

结语

今天的内容到这里就结束了，我们来回顾下都聊了哪些内容：
首先是回顾了递归求解斐波那契数列的问题，通过“记忆”优化了递归的执行速度，但是增加了空间复杂度。
然后为了更高效，我们引入了迭代，虽然我并不鼓励大家记忆概念和定义，但是你要明白相似概念的区别。
最后我们通过迭代的方式求解斐波那契数列，实现了 O(n) 复杂度。当然，斐波那契数列还有 $O(\log\_{}{n})$ 的解法，不过这不是我们今天的内容。