LeetCode 1382. 将二叉搜索树变平衡（中序遍历+二分递归）

1. 题目

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是平衡的。

如果有多种构造方法，请你返回任意一种。

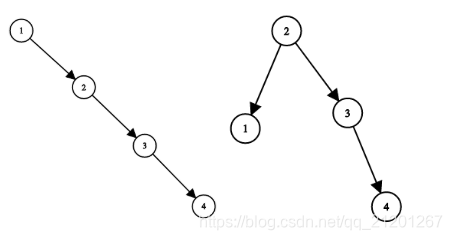
在这里插入图片描述

示例
输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。提示：
树节点的数目在 1 到 10^4 之间。
树节点的值互不相同，且在 1 到 10^5 之间。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/balance-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

先中序遍历，是有序的，存入vector
对 vector 二分递归，建立平衡二叉搜索树

class Solution {
public:TreeNode* balanceBST(TreeNode* root) {if(!root)return root;stack<TreeNode*> s;vector<TreeNode*> v;TreeNode* tp;while(root || !s.empty()){while(root){s.push(root);root = root->left;}tp = s.top();s.pop();root = tp->right;tp->left = NULL;tp->right = NULL;v.push_back(tp);}return build(v,0,v.size()-1);}TreeNode* build(vector<TreeNode*>& v, int l, int r){if(l > r)return NULL;int mid = l+((r-l)>>1);TreeNode* root = v[mid];root->left = build(v,l,mid-1);root->right = build(v,mid+1,r);return root;}
};