【0】README

1） 本文部分内容转自 数据结构与算法分析，旨在理解 高级数据结构实现——自顶向下伸展树 的基础知识；
2） 源代码部分思想借鉴了数据结构与算法分析，有一点干货原创代码，for original source code, please visit https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter12/p345_topdown_splay_tree
3） you can also refer to the link http://www.cnblogs.com/huangxincheng/archive/2012/08/04/2623455.html
4） for basic splay tree , please visit http://blog.csdn.net/PacosonSWJTU/article/details/50525435

---

【1】自顶向下伸展树相关

1）problem+solution

• 1.1）problem： 普通伸展树的展开操作需要从根沿树往下的一次遍历， 以及而后的从底向上的一次遍历。（详情，参见： http://blog.csdn.net/pacosonswjtu/article/details/50525435） 这可以通过保存一些父指针来完成， 或者通过将访问路径存储到一个栈中来完成。 但遗憾的 是， 这两种方法均需要大量的开销 ；
• 1.2）solution： 本节中， 我们指出如何在初始访问路径上施行一些旋转。结果得到在时间中更快的过程，只用到 O（1）的额外空间， 但却保持了 O(logN) 的摊还时间界；（干货——伸展树是基于AVL树的， 在AVL的基础上引入伸展树的目的是保持他的摊还时间界为 O（logN））

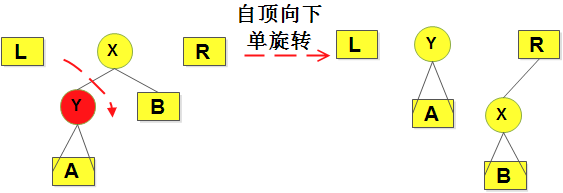
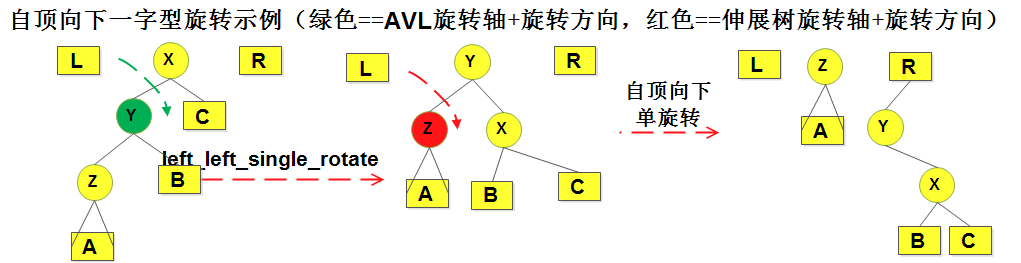
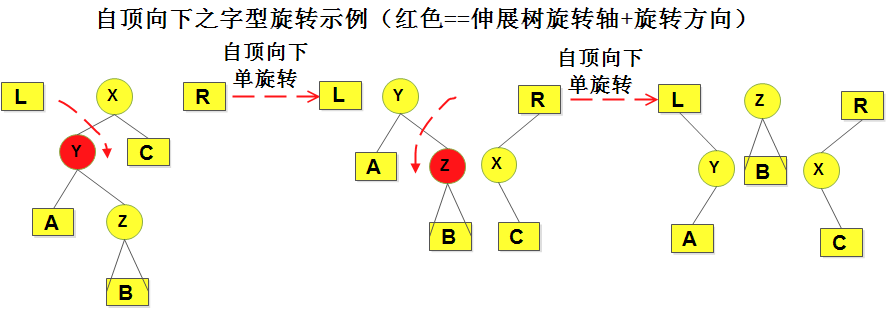
2）对伸展树的自顶向下的旋转操作：（单旋转+一字型旋转+之字型旋转）

• 2.1）这种伸展方式会把树切成三份，L树，M树，R树，考虑的情况有：单旋转，“一字型”旋转，“之字形”旋转。起初左树（L） 和 右树（R）均为空（NULL）；
  
  
  

---

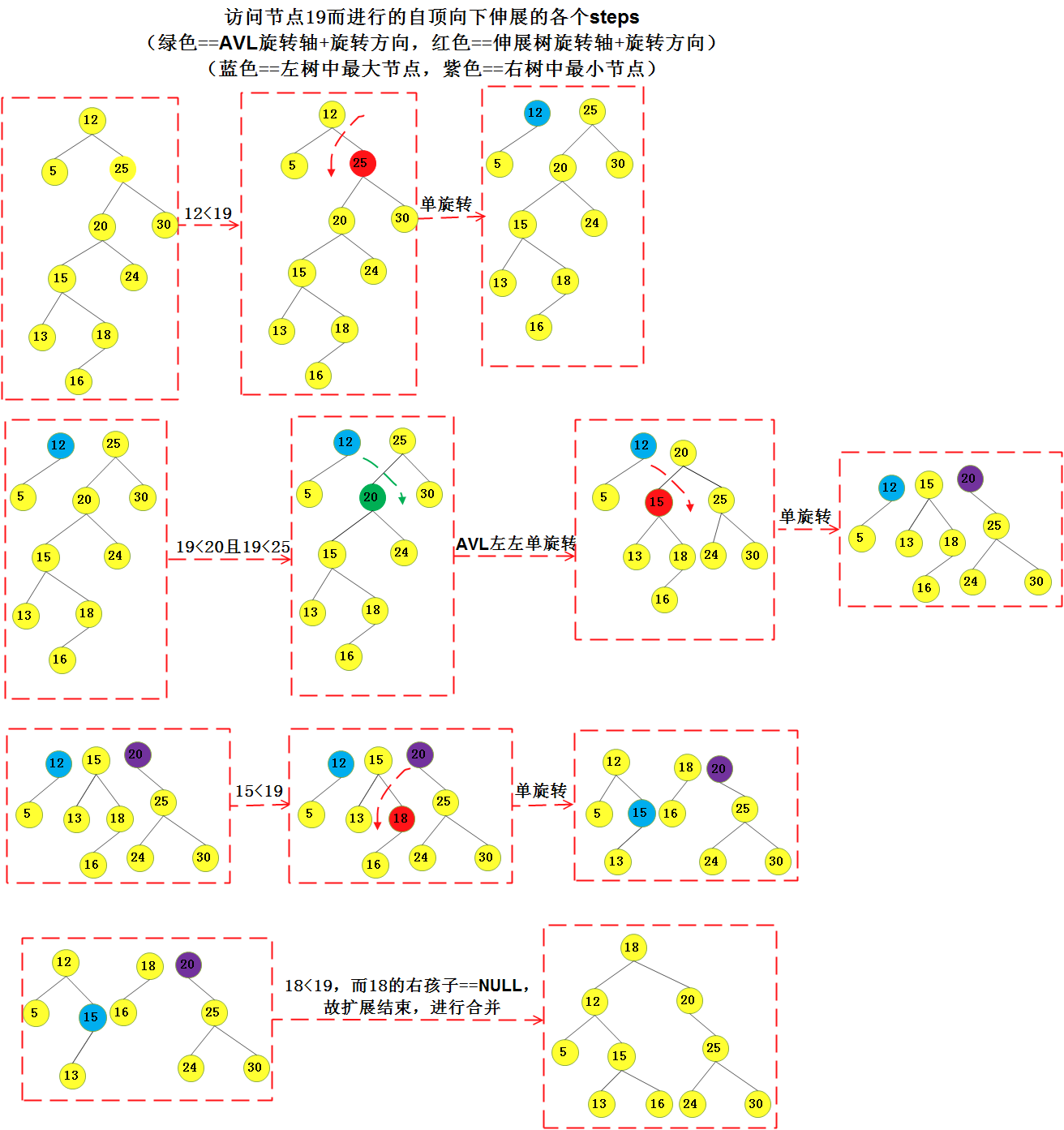
3）看个荔枝：

• 3.1）splay + deleting opeartions：
  

---

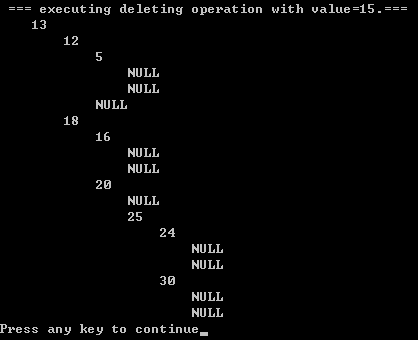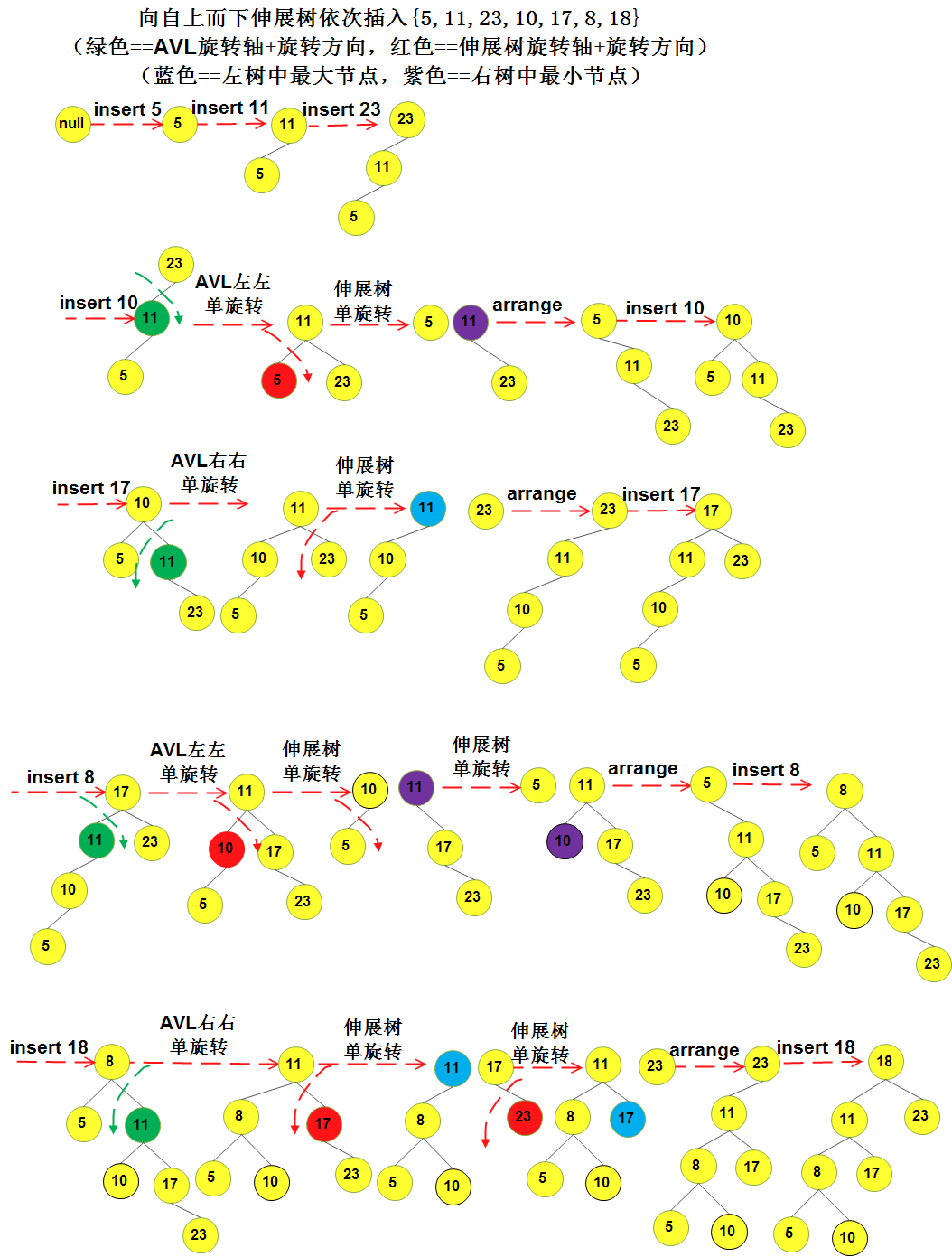
• 3.2）inserting opeartions：
  

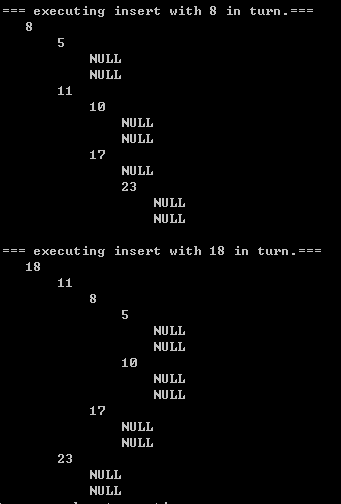4）source code at a glance

#include "topdown_splay_tree.h" // allocate memory for new node.
Node makeNode(int value)
{Node node;node = (Node)malloc(sizeof(struct Node));if(!node){Error("failed makeNode, for out of space !");return NULL;}node->left = NULL;node->right = NULL; node->value = value;return node;
}// left left single rotate
TopDownSplayTree left_left_single_rotate(TopDownSplayTree root)
{       TopDownSplayTree temp;temp = root; // 1st steproot = root->left; // 2nd steptemp->left = root->right; // 3rd steproot->right = temp; // 4th stepreturn root;
}// right_right_single_rotate
TopDownSplayTree right_right_single_rotate(TopDownSplayTree root)
{       TopDownSplayTree temp;temp = root; // 1st steproot = root->right; // 2nd steptemp->right = root->left; // 3rd steproot->left = temp; // 4th step  return root;
}// performing splay operations 
TopDownSplayTree topdown_splay(int value, TopDownSplayTree middle)
{struct Node plusTree;   Node leftTreeMax;   Node rightTreeMin;leftTreeMax = &plusTree;rightTreeMin = &plusTree;while(value != middle->value){   if(middle->value < value)  // the new node is greater.{    if(middle->right == NULL){break;}else if(middle->right->value < value && middle->right->right){middle = right_right_single_rotate(middle);}           leftTreeMax->right = middle;leftTreeMax = middle;middle = middle->right;     leftTreeMax->right = NULL;}if(middle->value > value) // the new node is less.{       if(middle->left == NULL){break;}else if(middle->left->value > value && middle->left->left){middle = left_left_single_rotate(middle);}rightTreeMin->left = middle;rightTreeMin = middle;middle = middle->left;rightTreeMin->left = NULL;}   }leftTreeMax->right = middle->left;rightTreeMin->left = middle->right;middle->left = plusTree.right;middle->right = plusTree.left;return middle;
}// delete the root of the  TopDownSplayTree
TopDownSplayTree deleteNode(int value, TopDownSplayTree root)
{TopDownSplayTree newroot;if(root == NULL) {return root;}else // the splay tree is not null{root = topdown_splay(value, root);if(root->value == value)  // find the node with given value.{ if(root->left == NULL){newroot = root->right;}else{newroot = root->left;// perform splay again with value towards the left subtree which is not null.newroot = topdown_splay(value, newroot);newroot->right = root->right; }free(root);root = newroot;}       }   return root;
}// insert the node with value into the TopDownSplayTree
TopDownSplayTree insert(int value, TopDownSplayTree root)
{TopDownSplayTree node;node = makeNode(value);      if(root == NULL) // the splay tree is null{return node;}else // the splay tree is not null{root = topdown_splay(value, root);if(root->value > value)  {node->left = root->left;node->right = root;root->left = NULL;root = node;            }else if(root->value < value)  {node->right = root->right;root->right = NULL;node->left = root;          root = node;}else            {return root;}}   return root;
}// test for insert operation.
int main1()
{TopDownSplayTree root;  int data[] = {5, 11, 23, 10, 17};int size = 5;int i;printf("\n === executing insert with {5, 11, 23, 10, 17} in turn.=== \n");root = NULL;for(i=0; i<size; i++){root = insert(data[i], root);printPreorder(1, root); }       printf("\n === executing insert with 8 in turn.=== \n");root = insert(8, root);printPreorder(1, root);     printf("\n === executing insert with 18 in turn.=== \n");root = insert(18, root);printPreorder(1, root);return 0;
}// test for splay operation and deleting operation.
int main()
{   TopDownSplayTree root;TopDownSplayTree temp;printf("\n ====== test for splaying operation====== \n");printf("\n === original tree is as follows.=== \n");root = makeNode(12); // root = 12temp = root;temp->left = makeNode(5);temp->right = makeNode(25);temp = temp->right;  // root = 25temp->left = makeNode(20);temp->right = makeNode(30);temp = temp->left;  // root = 20temp->left = makeNode(15);temp->right = makeNode(24);temp = temp->left;  // root = 15temp->left = makeNode(13);temp->right = makeNode(18);temp = temp->right;  // root = 18temp->left = makeNode(16);  printPreorder(1, root);printf("\n === executing splay operation with finding value=19.=== \n");root = topdown_splay(19, root);printPreorder(1, root);  printf("\n === executing deleting operation with value=15.=== \n");root = deleteNode(15, root);printPreorder(1, root);  return 0;
}// analog print node values in the binominal tree, which involves preorder traversal. 
void printPreorder(int depth, TopDownSplayTree root)
{           int i;if(root) {       for(i = 0; i < depth; i++)printf("    ");printf("%d\n", root->value);            printPreorder(depth + 1, root->left);                                   printPreorder(depth + 1, root->right);} else{for(i = 0; i < depth; i++)printf("    ");printf("NULL\n");}
}