2025年五一数学建模竞赛 A题

基于历史数据与模式识别的道路车流量推测模型研究

摘要

交通拥堵是现代城市面临的严峻挑战，准确预测道路车流量对于交通管理、信号配时优化和出行规划至关重要。本文聚焦于利用有限的历史观测数据和已知的交通流模式，推测特定路段（包括主路和多个支路）的详细车流量变化。通过构建和应用多种数学模型，旨在解决不同交通流特征下的车流量推测问题，并探讨数据误差和采样策略对推测精度的影响。

针对问题一：本文利用线性回归和分段线性回归模型，根据支路车流量的线性增长和先增后减趋势，推测了特定时间段内两条支路的车流量函数。

针对问题二：本文将模型应用扩展至四条具有不同变化规律（稳定、线性增长、线性减少、周期性）的支路，分别采用常数模型、线性模型和周期函数模型（如正弦函数或傅里叶级数）进行拟合与推测。

针对问题三：本文特别考虑了交通信号灯对车流量的周期性影响，通过模运算分析周期内流量模式，并应用傅里叶级数等周期模型对受信号灯控制的支路车流量进行建模。

针对问题四：本文探讨了观测数据中可能存在的误差问题，通过分析拟合残差来评估误差特性，并提出了数据平滑、鲁棒拟合等方法来推测更接近“实际”的车流量。

针对问题五：本文从模型复杂度和信息论角度分析了确定车流量函数所需的最少数据记录时刻问题，强调了在关键特征点（如起止点、极值点、转折点）进行采样以及满足奈奎斯特采样定理的重要性

最后，本文分析了模型的优缺点，讨论了模型的改进方向并对模型进行了简单的推广。

一、问题的背景和重述

1.1问题的背景

随着城市化进程加速和机动车保有量持续增长，交通拥堵已成为制约城市运行效率和影响居民生活质量的普遍问题。精确掌握道路交通流量的时变规律，是实施有效交通管理和控制、优化信号灯配时、提供智能出行诱导服务以及规划交通基础设施的基础。然而，在实际应用中，交通数据的获取往往受限于监测设备的布设范围和成本，可能仅能获得部分路段（如主干道）或汇总性的数据。如何利用这些有限的信息，结合对交通流行为模式的理解，来推测和还原更详细的路网交通状态（例如各支路的具体流量），是一个具有重要理论价值和实际应用意义的研究课题。

1.2问题的重述

本文旨在研究如何基于给定的历史数据和交通流模式描述，建立数学模型以推测道路（特别是支路）的车流量函数。具体研究问题如下：
问题1：已知主路历史数据和两条支路的车流量变化趋势（支路1线性增长，支路2先线性增长后线性减少），推测这两条支路在特定时间段（6:58至8:58）的车流量函数。
问题2：推测四条具有不同变化规律的支路的车流量函数：支路1稳定，支路2线性增长，支路3线性减少，支路4呈周期性波动。
问题3：在一个受交通信号灯（周期为18个时间单位）影响的特殊路段，推测支路1、2和受控的支路3的车流量函数。
问题4：考虑到监测数据可能存在误差，如何在包含误差的数据基础上，推测“实际”的车流量，并可能描述误差的特性。
问题5：为了能够准确推测出上述问题中描述的各种车流量函数，确定最少需要记录哪些时刻的数据点。

二、问题的分析

本系列问题旨在通过数学建模的方法，解决基于不完全信息和特定模式描述下的交通流量推测问题。核心在于为不同特征的交通流选择合适的数学函数进行拟合与预测，并考虑实际应用中的复杂因素。
针对问题1：此问题是基础的函数拟合应用。关键在于根据“线性增长”和“先增后减”的描述选择正确的函数形式（一次多项式和分段一次多项式），并利用（可能需要从主路数据分离出的）支路数据通过最小二乘法估计模型参数。需要进行时间坐标的转换，并确定分段模型的转折点。
针对问题2：此问题将模型库扩展到常数、负斜率线性函数以及周期函数。周期性流量的建模是难点，需要选择合适的周期函数（如正弦函数或傅里叶级数），并估计其振幅、频率、相位和均值等参数。可能需要非线性拟合技术或频谱分析辅助。
针对问题3：此问题引入了外部周期性干扰（交通信号灯）。关键在于识别和建模这种由信号灯控制产生的特定周期（18个时间单位）的流量波动模式。可以通过分析时间模周期下的流量分布来选择合适的周期函数（如傅里叶级数或自定义脉冲函数）进行拟合。
针对问题4：此问题关注数据质量和模型鲁棒性。需要分析模型拟合后的残差（观测值-拟合值），以判断误差的性质（随机噪声还是系统偏差）和大小。可以采用数据平滑技术（如移动平均、滤波器）预处理数据，或使用鲁棒回归方法减少异常值的影响，从而得到更可靠的“真实”流量估计。
针对问题5：此问题涉及采样理论和模型辨识度。最少所需数据点数与模型的自由参数数量相关。理论上k个参数需要至少k个独立数据点。但为了捕捉函数形态和保证拟合稳健性，需要更多且分布在关键位置（如起止点、极值点、趋势转折点）的数据。对于周期信号，采样频率需满足奈奎斯特准则以避免混叠。

三、模型假设

1、数据代表性假设： 提供的历史数据能够准确反映相应时间段内典型的交通流量变化模式。

2、模式一致性假设： 问题中描述的各支路交通流模式（如线性增长、周期性等）在整个分析时间段内是持续有效的。

3、时间连续性与离散测量假设： 假设交通流量随时间连续变化（或在宏观层面可视为连续），但我们获得的是离散时间点的测量数据。

4、参数恒定性假设： 在所分析的时间段内，描述交通流模式的模型参数（如增长率、周期、振幅等）保持不变。

5、时间坐标转换假设： 所有涉及的时间点都可以无歧义地转换为统一的数值时间坐标（例如，从起始时刻计数的分钟数）用于计算。

6、信号灯影响规律性假设（针对问题3）： 交通信号灯的周期（18个时间单位）是精确的，其对支路3车流量的影响模式在每个周期内是稳定重复的。

四、符号及变量说明

五、模型的建立与求解

问题一：基于线性回归的支路车流量推测

解题思路：

• 根据支路1的线性增长和支路2的先增后减趋势，分别建立线性函数和分段线性函数模型。
• 利用主路历史数据，通过最小二乘法拟合支路车流量函数。
• 确定分段模型的转折点，并调整参数以保证函数的连续性。

解题过程：

1. 数据可视化，找到支路2的峰值时间点。
2. 分别对支路1和支路2建立线性模型和分段线性模型。
3. 通过假设和启发式方法确定支路1的增长率和截距。
4. 根据连续性条件，求解支路2的参数。
5. 输出支路1和支路2的车流量函数表达式，并进行可视化。

问题二：组合流量模型的构建与参数估计

解题思路：

• 构建包含稳定流、线性增长流和周期性流的组合流量模型。
• 考虑支路1和支路2的2分钟时延，通过非线性优化方法估计所有未知参数。
• 使用遍历搜索法确定未知转折点，并优化模型参数。

解题过程：

1. 定义各支路流量模型的形式，包括稳定流、线性增长流和周期性流。
2. 构建总流量模型，考虑支路的时延。
3. 使用非线性优化方法（如lsqnonlin）估计模型参数。
4. 遍历搜索未知转折点，找到使误差最小的转折点。
5. 输出各支路流量函数表达式，并进行可视化。

问题三：考虑交通信号灯的复杂流量模型

解题思路：

• 引入交通信号灯的周期性影响，建立考虑信号灯周期性开关效应的流量模型。
• 使用整数参数遍历搜索与非线性最小二乘相结合的混合优化策略，估计模型参数。
• 考虑支路1和支路2的2分钟时延，以及支路3受交通灯控制的特性。

解题过程：

1. 定义交通信号灯的状态函数，确定绿灯和红灯的时间区间。
2. 构建各支路流量模型，考虑交通信号灯的周期性影响。
3. 使用混合优化策略，遍历搜索整数参数（如转折点），并结合非线性优化估计连续参数。
4. 输出各支路流量函数表达式，并进行可视化。

问题四：考虑数据误差的流量模型优化

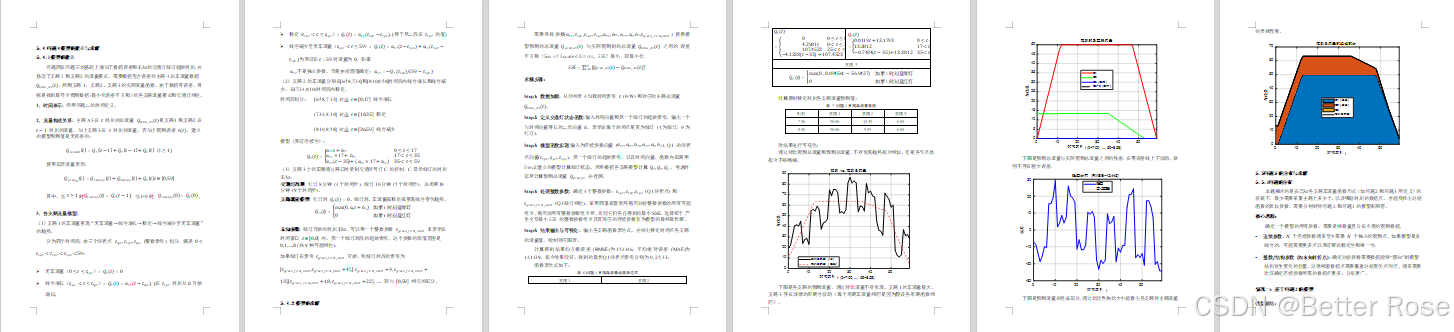
解题思路：

• 在问题三的基础上，考虑数据误差和未知的交通灯绿灯起始时刻。
• 引入参数边界约束、目标函数惩罚项，利用先验知识改进初始值猜测。
• 使用增强的混合优化算法对数据进行拟合。

解题过程：

1. 定义各支路流量模型，考虑数据误差和未知的交通灯绿灯起始时刻。
2. 引入参数边界约束和目标函数惩罚项，优化模型参数。
3. 使用混合优化策略，遍历搜索整数参数（如转折点和绿灯起始时刻），并结合非线性优化估计连续参数。
4. 输出各支路流量函数表达式，并进行可视化。

问题五：最少数据采样问题分析

解题思路：

• 分析模型参数辨识度，确定各支路流量函数所需的最少数据采样点。
• 通过理论分析和模拟测试，验证数据点的分布和数量对模型拟合的影响。

解题过程：

1. 理论分析模型参数与数据点的关系，确定最少数据点需求。
2. 使用代码测试不同数据子集的拟合效果，逐步减少数据点并观察误差变化。
3. 根据误差阈值，确定最少观测数据点的数量和具体时刻。

关键代码

完整论文，请看下方