模电乱写

二极管

理想模型和恒压降模型非常简单。

交流小信号模型就是假设 \(u_i\) 在一个非常小的范围震荡。

然后因为 \(i(u)\) 是连续的，你在看 \(\lim \limits_{\Delta u\to 0} i(u+\Delta u)=i(u),\) 所以换来换去都是一个点。

于是问题解决了，限制是幅值很小(\(\Delta u\to 0\))，由于物理条件限制频率不能过大。

以及 \(i(u)=I_s(e^{\frac{u}{u_T}}-1),u_T\) 是一个只和温度 \(T\) 相关的量。

PN结

一边是空穴多一边是电子多，两个东西放一块会扩散。导致边缘部分空穴被电子填满不导电了。需要足够高的电压打穿这一层才能继续导电。

---

含二极管电路分析，先断开二极管，分析正负电压，如果大于压降就是通，通了以后只过电流。

---

稳压二极管主要考虑反偏，过了截止有一段跟恒压降很接近的，

这一段 \(u\to u_0\) 常数，所以对的电压不是 \(0\) 就是 \(u_0\).

三极管

发射极正偏集电结反偏。

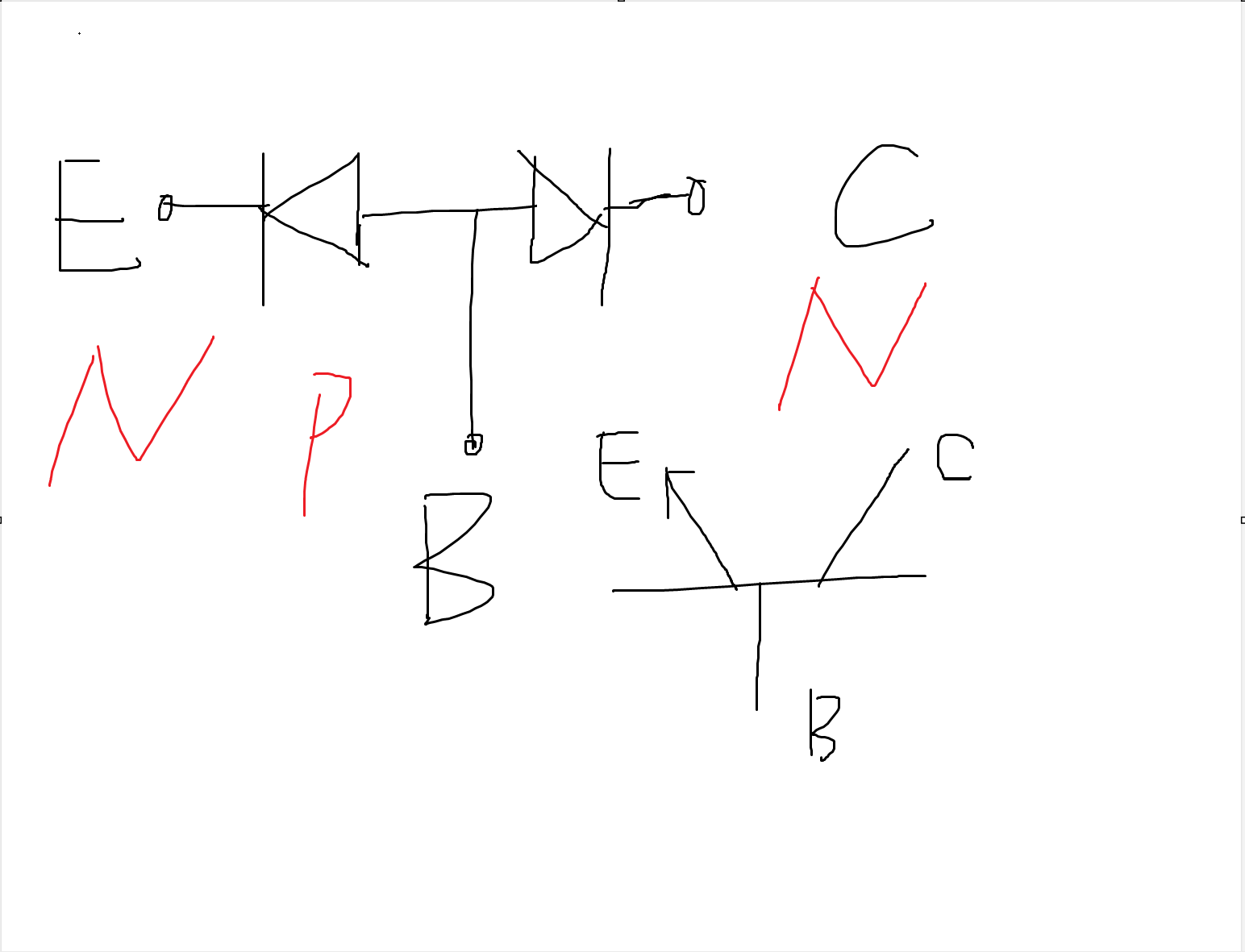
指标

\(\beta=\frac{I_C}{I_B},\alpha=\frac{I_C}{I_E}\)

两个指标一个共射一个共基，都是集电结输出。典型的输出比输入。

\(\beta=\frac{\alpha}{1-\alpha},\alpha\to 1\Rightarrow \beta\to \infty\)

事情似乎天生如此，\(I_B 10mA\) 别的都可以很大，限于物理条件 \(\beta\space 10^2\) 差不多。

输入电阻 \(R_i=\frac{U_i}{I_i},R_o=\frac{U_o}{I_o}\)

放大指标 \(A_u=\frac{U_o}{U_i}\)

最大不失真电压 \(U_{om}\) 对应功率 \(P_{om}\) 效率 \(\eta=\frac{P_{om}}{P_v}\)

静态工作点 \(Q\) 指标 \(I_{BQ},U_{BEQ},I_{CQ},U_{CEQ}\)

算指标先 \(Q\) 再 \(R_i,R_o,A_u\) 比较套路

图像

先看直流再看交流。

以基本共射为例。输出 \(u_{CE}\) 不变，考察输入电流和电压的关系\(i_B(u_{BE})\)。

\(B\)和\(E\)之间的部分本质上是个二极管。所以这一部分就是非常类似于二极管一样的东西。

考察 \(i_C(u_{CE})\) 的话其实差不多类似，但是会出现削弱，所以电流不是无限涨下去。

组态判断

输入两个端口输出两个端口三极管三个级。

哪一极接了两个端口就是共哪极的组态。

工作点分析

先写直流再写交流。

直流的等效是电容断开，交流的等效是电源电容变导线。

---

以下面这个为例：

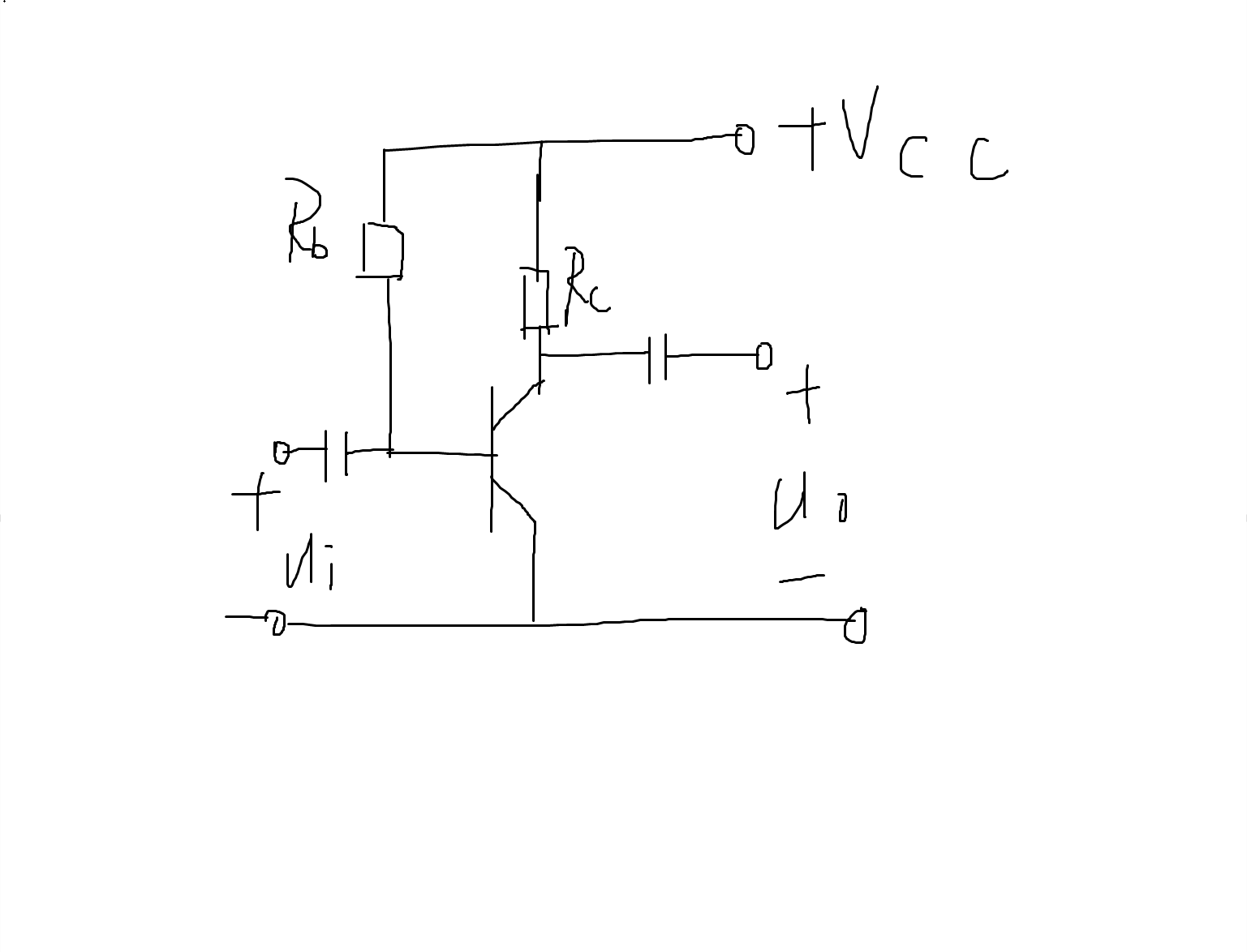
直流等效电路

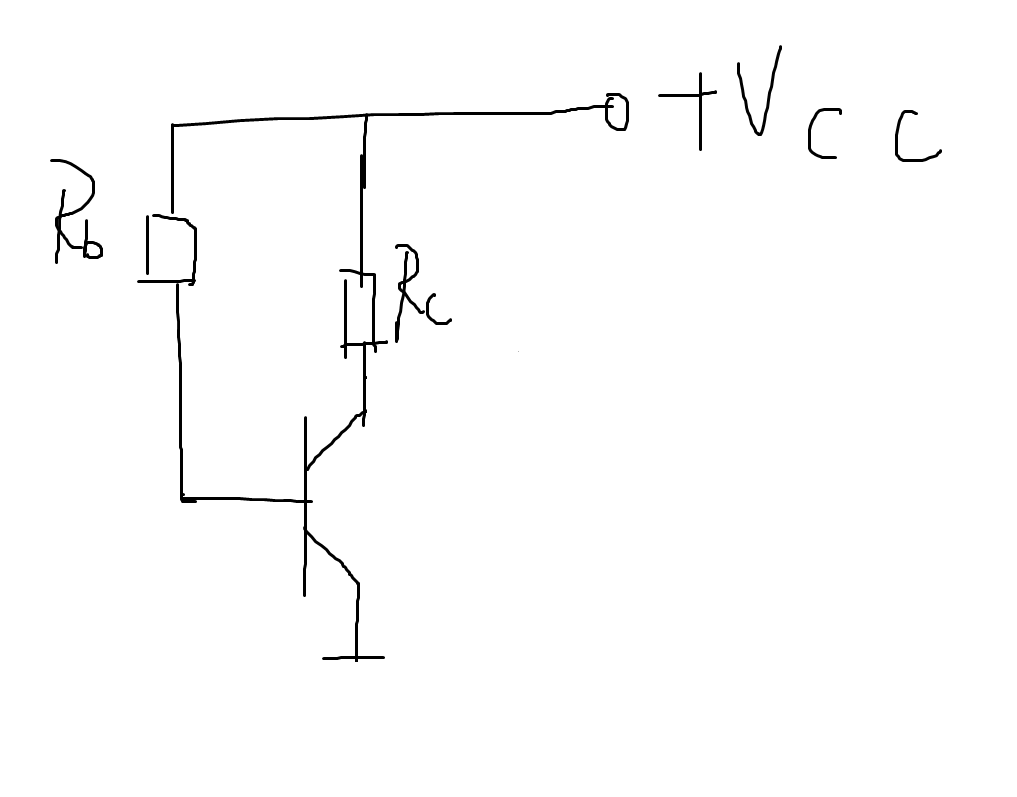
先算基极比较好算，后面直接有集电极。

\(I_{BQ}=\frac{V_{CC}-U_{BEQ}}{R_B},U_{BEQ}\) 是常量，因为 \(BE\) 之间是二极管。

\(I_{CQ}=\beta I_{BQ}\)

\(U_{CEQ}=V_{CC}-R_C\cdot I_{CQ}\)

这就算完了，如果有串并联没有关系，等效一下就可以。

还有图解，主要是画 \(I_{CQ}(U_{CEQ})\) 的图像，给定 \(I_{BQ}\) 对线找交点就可以。

这里给下 \(I_{CQ}(U_{CEQ})\) 的式子。

\[I_{CQ}=\frac{V_{CC}-\beta(\frac{V_{CC}-U_{BEQ}}{R_B}}{R_C}). \]

有点复杂不展开了。

---

交流等效电路

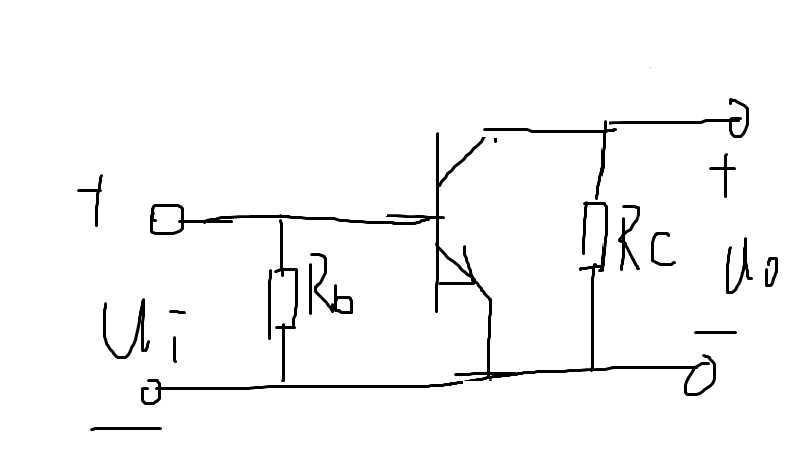
这个感觉没有一条非常合理的支路能拿来分析的，需要对三极管做个等效。

考虑输入输出特性、连接方式和 \(\beta\) 指标。

输入输出特性是在造电阻，\(\beta\) 指标是受控源。

但是你右边不能只是受控源，因为要考虑输出特性，是个电阻并联受控源。

所以一个最简单的模型

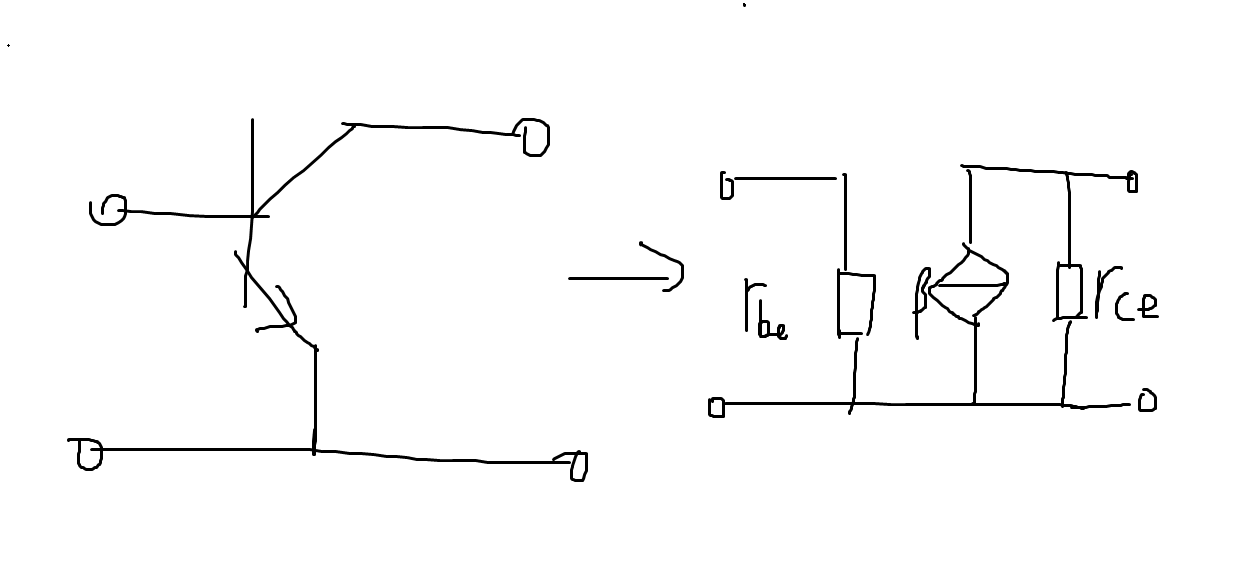
剩下就是算。