实验三 加法器与ALU
加法器
一位全加器的设计相对简单,请读者根据电路图自行思考如果设计一个串行进位加法器电路。 串行加法器速度很慢,因为进位必须从最低位传至最高位。要想构建速度较快的加法器,就要利用附加逻辑,提前算出进位信息,这就是先行进位加法器的设计思想,先行进位加法有几种常用的算法,感兴趣的同学可以查找资料阅读。
1. 先行进位加法器设计
先行进位加法器(Carry Lookahead Adder, CLA)通过提前计算进位信号来提高加法速度。
1.1 先行进位原理
定义两个中间变量:
●生成信号(Gi):Gi = Ai & Bi
●传播信号(Pi):Pi = Ai ^ Bi
进位信号可以表示为:
Ci+1 = Gi | (Pi & Ci)展开后可以得到:
C1 = G0 | (P0 & C0)
C2 = G1 | (P1 & G0) | (P1 & P0 & C0)
C3 = G2 | (P2 & G1) | (P2 & P1 & G0) | (P2 & P1 & P0 & C0)
C4 = G3 | (P3 & G2) | (P3 & P2 & G1) | (P3 & P2 & P1 & G0) | (P3 & P2 & P1 & P0 & C0)
1.2 4位先行进位加法器实现
module carry_lookahead_adder_4bit(input [3:0] A, B,input Cin,output [3:0] Sum,output Cout
);wire [3:0] G, P;wire [4:0] C;// 计算生成和传播信号assign G = A & B;assign P = A ^ B;// 计算进位assign C[0] = Cin;assign C[1] = G[0] | (P[0] & C[0]);assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & C[0]);assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & C[0]);assign C[4] = G[3] | (P[3] & G[2]) | (P[3] & P[2] & G[1]) | (P[3] & P[2] & P[1] & G[0]) | (P[3] & P[2] & P[1] & P[0] & C[0]);// 计算和assign Sum = P ^ C[3:0];assign Cout = C[4];
endmodule
1.3 先行进位加法器特点
1.优点:
a.延迟与位数对数成正比(O(log n))
b.适合高速运算
c.可扩展性强(可构建多级先行进位)
2.缺点:
a.逻辑复杂度高
b.占用资源多
c.功耗较大
2. 其他高速加法器结构
2.1 超前进位加法器(CLA)扩展
对于更多位数的加法器,可以采用多级先行进位结构:
●组内先行进位
●组间先行进位
2.2 条件求和加法器(Conditional Sum Adder)
通过并行计算所有可能的进位情况,然后根据实际进位选择正确结果。
2.3 进位选择加法器(Carry Select Adder)
将加法器分成若干段,每段同时计算进位为0和1两种情况,然后根据实际进位选择正确结果。
3. 性能比较
| 加法器类型 | 延迟特性 | 资源消耗 | 适用场景 |
|---|---|---|---|
| 串行进位加法器 | O(n) | 低 | 低速、低功耗设计 |
| 先行进位加法器 | O(log n) | 高 | 高速运算 |
| 进位选择加法器 | O(√n) | 中 | 中等速度需求 |
| 条件求和加法器 | O(log n) | 很高 | 极高速运算 |
4. 多功能加减法加法器设计
4.1 设计概述
功能需求
●支持n位二进制数的加法和减法运算
●通过控制信号选择运算模式
●正确输出运算结果和状态标志:
○进位标志(Carry)
○溢出标志(Overflow)
○零标志(Zero)
○符号标志(Sign)
技术方案
●采用补码表示有符号数
●减法通过"加补码"实现
●使用先行进位(Carry Lookahead)优化性能
4.2 完整Verilog实现
module arithmetic_unit #(parameter WIDTH = 32
)(input [WIDTH-1:0] a, // 操作数Ainput [WIDTH-1:0] b, // 操作数Binput sub, // 运算选择: 0=加法, 1=减法output [WIDTH-1:0] result,// 运算结果output carry, // 进位标志(无符号数溢出)output overflow, // 溢出标志(有符号数溢出)output zero, // 零标志output sign // 符号标志
);// 中间信号wire [WIDTH-1:0] b_operand;wire carry_in;wire [WIDTH:0] sum; // 包含进位位的扩展和// 减法转换为补码加法assign b_operand = sub ? ~b : b;assign carry_in = sub ? 1'b1 : 1'b0;// 核心加法器assign sum = {1'b0, a} + {1'b0, b_operand} + {{WIDTH{1'b0}}, carry_in};// 结果和标志位assign result = sum[WIDTH-1:0];assign carry = sum[WIDTH];// 溢出检测: 有符号数溢出发生在:// 1. 正数+正数=负数// 2. 负数+负数=正数assign overflow = (a[WIDTH-1] == b_operand[WIDTH-1]) && (result[WIDTH-1] != a[WIDTH-1]);// 零标志assign zero = (result == {WIDTH{1'b0}});// 符号标志assign sign = result[WIDTH-1];endmodule
4.3 测试验证
module tb_arithmetic_unit;reg [31:0] a, b;reg sub;wire [31:0] result;wire carry, overflow, zero, sign;arithmetic_unit uut (.a(a),.b(b),.sub(sub),.result(result),.carry(carry),.overflow(overflow),.zero(zero),.sign(sign));initial begin// 测试加法sub = 0;a = 32'h0000_000F; b = 32'h0000_0001; #10; // 15+1=16a = 32'h7FFF_FFFF; b = 32'h0000_0001; #10; // MAX_INT+1 (溢出)// 测试减法sub = 1;a = 32'h0000_000F; b = 32'h0000_0001; #10; // 15-1=14a = 32'h8000_0000; b = 32'h0000_0001; #10; // MIN_INT-1 (溢出)// 测试特殊值a = 32'h0000_0000; b = 32'h0000_0000; #10; // 0+0=0a = 32'hFFFF_FFFF; b = 32'h0000_0001; sub=0; #10; // -1+1=0$finish;end
endmodule
5. 减法运算溢出判断的正确实现分析
5.1 方法一与方法二的关键区别
两种方法的核心差异在于如何处理进位输入(Cin):
1.方法一:
a.先对B进行按位取反(当Cin=1时)
b.然后在加法器中统一加Cin
2.方法二:
a.先对B进行按位取反并立即加上Cin
b.然后在加法器中直接相加
5.2 最小负数情况的特殊问题
对于n位有符号数:
●最小负数为 -2^(n-1)(如8位的-128,表示为 10000000)
●当B是最小负数时,-B 在数学上应该是 2^(n-1),但这超出了n位有符号数的表示范围
5.3 详细分析
方法一:
assign t_no_Cin = {n{ Cin }}^B; // Cin=1时取反B
assign {Carry,Result} = A + t_no_Cin + Cin; // 统一加Cin
assign Overflow = (A[n-1] == t_no_Cin[n-1]) && (Result[n-1] != A[n-1]);
问题:
●当B是最小负数时,t_no_Cin = ~B = 011...11(正的最大值)
●加Cin会导致进位传播,可能影响溢出判断
●不能正确处理 A - (-2^(n-1)) 的情况(即 A + 2^(n-1))
方法二:
assign t_add_Cin = ({n{Cin}}^B) + Cin; // 先取反并立即加Cin
assign {Carry, Result} = A + t_add_Cin;
assign Overflow = (A[n-1] == t_add_Cin[n-1]) && (Result[n-1] != A[n-1]);
优点:
●当B是最小负数时:
○{n{Cin}}^B = ~B = 011...11
○立即 + Cin 得到 100...00(即 -B 的正确补码表示)
●正确处理所有边界情况,包括 A - (-2^(n-1))
5.4 具体案例验证(以8位为例)
测试 A - B 其中 B = -128 (10000000):
1.方法一:
a.t_no_Cin = ~10000000 = 01111111
b.A + 01111111 + 1 = A + 10000000(数学上正确)
c.但溢出判断会比较 A[7] 和 01111111[7](总是不同),导致溢出检测失效
2.方法二:
a.t_add_Cin = ~10000000 + 1 = 01111111 + 1 = 10000000
b.A + 10000000(完全符合减法语义)
c.溢出判断比较 A[7] 和 10000000[7](能正确检测符号变化)
结论
方法二是正确的实现,因为它:
1.正确处理了减数为最小负数时的特殊情况
2.保持了补码运算的数学一致性
3.能准确检测所有溢出情况
方法一在常规情况下可以工作,但在边界条件(特别是B为最小负数时)会出现问题。在实际硬件设计中,必须使用方法二这种实现来确保所有情况下的正确性。
6. 四位补码加减法器
波形仿真
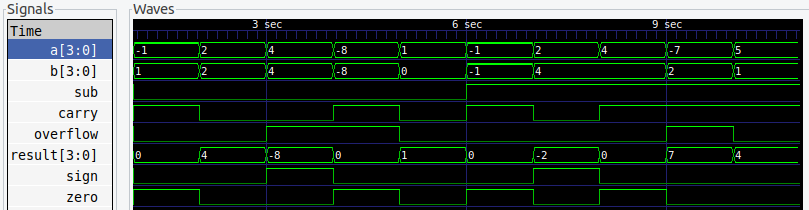
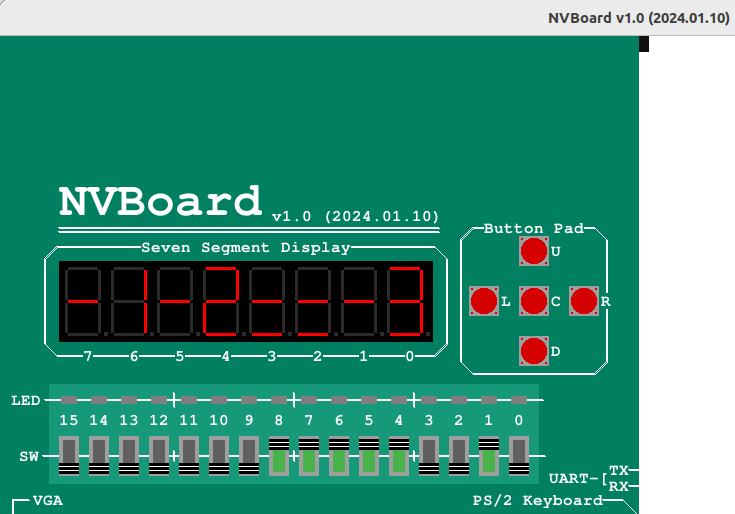
top.nxdc
top=topa (SW7, SW6, SW5, SW4)
b (SW3, SW2, SW1, SW0)
sub (SW8)segs (SEG7A, SEG7B, SEG7C, SEG7D, SEG7E, SEG7F, SEG7G, DEC7P, SEG6A, SEG6B, SEG6C, SEG6D, SEG6E, SEG6F, SEG6G, DEC6P, SEG5A, SEG5B, SEG5C, SEG5D, SEG5E, SEG5F, SEG5G, DEC5P, SEG4A, SEG4B, SEG4C, SEG4D, SEG4E, SEG4F, SEG4G, DEC4P, SEG3A, SEG3B, SEG3C, SEG3D, SEG3E, SEG3F, SEG3G, DEC3P, SEG2A, SEG2B, SEG2C, SEG2D, SEG2E, SEG2F, SEG2G, DEC2P, SEG1A, SEG1B, SEG1C, SEG1D, SEG1E, SEG1F, SEG1G, DEC1P, SEG0A, SEG0B, SEG0C, SEG0D, SEG0E, SEG0F, SEG0G, DEC0P)
top.v
module top #(parameter WIDTH = 4
)(input [WIDTH-1:0] a, // 操作数Ainput [WIDTH-1:0] b, // 操作数Binput sub, // 运算选择output [63:0] segs // 6位数码管的段选信号(8位x6)
);// 算术运算单元wire [WIDTH-1:0] result;wire carry, overflow, zero, sign;arithmetic_unit #(WIDTH) u_arithmetic (.a(a),.b(b),.sub(sub),.result(result),.carry(carry),.overflow(overflow),.zero(zero),.sign(sign));// 各数码管段选信号生成wire [7:0] seg [0:7];// 第1-2位:操作数Aassign seg[0] = a[3] ? 8'b11111101 : 8'b11111111; // "-"或空wire [3:0] abs_a;assign abs_a = a[3] ? (a == 4'b1000 ? 4'h8 : // -8a == 4'b1001 ? 4'h7 : // -7a == 4'b1010 ? 4'h6 : // -6a == 4'b1011 ? 4'h5 : // -5a == 4'b1100 ? 4'h4 : // -4a == 4'b1101 ? 4'h3 : // -3a == 4'b1110 ? 4'h2 : // -2a == 4'b1111 ? 4'h1 : // -14'h0) : a;seg7_decoder u_seg0 (.bin(abs_a), .seg(seg[1]));// 第3位:运算符assign seg[2] = sub^b[3] ? 8'b11111101 : 8'b11111110; // "-"或"+"// 第4位:操作数B的绝对值wire [3:0] abs_b;assign abs_b = b[3] ? (b == 4'b1000 ? 4'h8 : // -8b == 4'b1001 ? 4'h7 : // -7b == 4'b1010 ? 4'h6 : // -6b == 4'b1011 ? 4'h5 : // -5b == 4'b1100 ? 4'h4 : // -4b == 4'b1101 ? 4'h3 : // -3b == 4'b1110 ? 4'h2 : // -2b == 4'b1111 ? 4'h1 : // -14'h0) : b;seg7_decoder u_seg2 (.bin(abs_b), .seg(seg[3]));// 第5-6位:等号"="assign seg[4] = 8'b11101101; // 显示g和c段assign seg[5] = 8'b11101101; // 显示g和c段// 第7位:符号位assign seg[6] = sign ? 8'b11111101 : 8'b11111111; // "-"或空// 第8位:结果绝对值wire [3:0] abs_result;assign abs_result = sign ? (result == 4'b1000 ? 4'h8 : // -8result == 4'b1001 ? 4'h7 : // -7result == 4'b1010 ? 4'h6 : // -6result == 4'b1011 ? 4'h5 : // -5result == 4'b1100 ? 4'h4 : // -4result == 4'b1101 ? 4'h3 : // -3result == 4'b1110 ? 4'h2 : // -2result == 4'b1111 ? 4'h1 : // -14'h0) : result;seg7_decoder u_seg5 (.bin(abs_result), .seg(seg[7]));// 合并所有段选信号assign segs = {seg[0], seg[1], seg[2], seg[3], seg[4], seg[5], seg[6], seg[7]};endmodule// 七段译码器模块
module seg7_decoder (input [3:0] bin,output reg [7:0] seg // a-g + dp
);always @(*) begincase(bin)4'h0: seg = 8'b00000011; // 04'h1: seg = 8'b10011111; // 14'h2: seg = 8'b00100101; // 24'h3: seg = 8'b00001101; // 34'h4: seg = 8'b10011001; // 44'h5: seg = 8'b01001001; // 54'h6: seg = 8'b01000001; // 64'h7: seg = 8'b00011111; // 74'h8: seg = 8'b00000001; // 84'h9: seg = 8'b00001001; // 9default: seg = 8'b11111111; // 全灭endcaseend
endmodule// 算术运算单元(保持不变)
module arithmetic_unit #(parameter WIDTH = 4
)(input [WIDTH-1:0] a,input [WIDTH-1:0] b,input sub,output [WIDTH-1:0] result,output carry,output overflow,output zero,output sign
);// 中间信号wire [WIDTH-1:0] b_operand;wire carry_in;wire [WIDTH:0] sum; // 包含进位位的扩展和// 减法转换为补码加法assign b_operand = sub ? ~b : b;assign carry_in = sub ? 1'b1 : 1'b0;// 核心加法器assign sum = {1'b0, a} + {1'b0, b_operand} + {{WIDTH{1'b0}}, carry_in};// 结果和标志位assign result = sum[WIDTH-1:0];assign carry = sum[WIDTH];// 溢出检测: 有符号数溢出发生在:// 1. 正数+正数=负数// 2. 负数+负数=正数assign overflow = (a[WIDTH-1] == b_operand[WIDTH-1]) && (result[WIDTH-1] != a[WIDTH-1]);// 零标志assign zero = (result == {WIDTH{1'b0}});// 符号标志assign sign = result[WIDTH-1];
endmodule
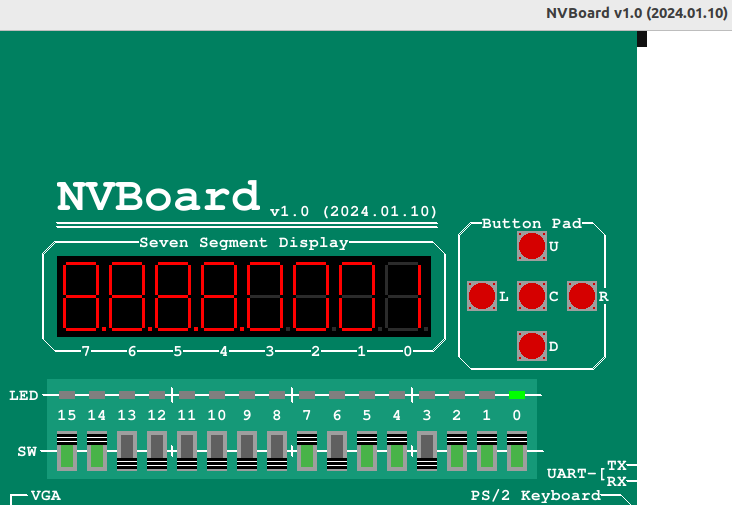
7.ALU
波形仿真

top.nxdc
top=topa (SW7, SW6, SW5, SW4)
b (SW3, SW2, SW1, SW0)
op (SW15, SW14, SW13)out (LD3, LD2, LD1, LD0)
segs (SEG3A, SEG3B, SEG3C, SEG3D, SEG3E, SEG3F, SEG3G, DEC3P, SEG2A, SEG2B, SEG2C, SEG2D, SEG2E, SEG2F, SEG2G, DEC2P, SEG1A, SEG1B, SEG1C, SEG1D, SEG1E, SEG1F, SEG1G, DEC1P, SEG0A, SEG0B, SEG0C, SEG0D, SEG0E, SEG0F, SEG0G, DEC0P)
top.v
module top #(parameter WIDTH = 4
)(input [WIDTH-1:0] a, // 操作数Ainput [WIDTH-1:0] b, // 操作数Binput [2:0] op, // 操作码output reg [WIDTH-1:0] out, // 运算结果output zero, // 零标志output carry, // 进位标志output overflow, // 溢出标志output [31:0] segs
);alu_4 #(WIDTH) u_alu(.a(a),.b(b),.op(op),.out(out),.zero(zero),.carry(carry),.overflow(overflow));// 各数码管段选信号生成wire [7:0] seg [0:3];seg7_decoder u_seg0 (.bin({{WIDTH-1{1'b0}}, out[3]}), .seg(seg[0]));seg7_decoder u_seg1 (.bin({{WIDTH-1{1'b0}}, out[2]}), .seg(seg[1]));seg7_decoder u_seg2 (.bin({{WIDTH-1{1'b0}}, out[1]}), .seg(seg[2]));seg7_decoder u_seg3 (.bin({{WIDTH-1{1'b0}}, out[0]}), .seg(seg[3]));assign segs = {seg[0], seg[1], seg[2], seg[3]};endmodulemodule alu_4 #(parameter WIDTH = 4
)(input [WIDTH-1:0] a, // 操作数Ainput [WIDTH-1:0] b, // 操作数Binput [2:0] op, // 操作码output reg [WIDTH-1:0] out, // 运算结果output zero, // 零标志output carry, // 进位标志output overflow // 溢出标志
);// 内部信号wire [WIDTH:0] add_result; // 加法结果(带进位)wire [WIDTH:0] sub_result; // 减法结果(带进位)wire [WIDTH-1:0] not_out, xor_out, and_out, or_out;wire signed_lt, unsigned_lt, eq;// 算术运算(统一处理带符号和无符号)assign add_result = {1'b0, a} + {1'b0, b};assign sub_result = {1'b0, a} + {1'b0, ~b} + 1;// 逻辑运算assign not_out = ~a;assign xor_out = a ^ b;assign and_out = a & b;assign or_out = a | b;// 比较运算assign eq = (a == b);assign unsigned_lt = sub_result[WIDTH]; // 无符号比较// 带符号比较逻辑wire same_sign = (a[WIDTH-1] == b[WIDTH-1]);wire overflow_sub = (a[WIDTH-1] != b[WIDTH-1]) && (sub_result[WIDTH-1] != a[WIDTH-1]);assign signed_lt = overflow_sub ? ~sub_result[WIDTH-1] : sub_result[WIDTH-1];// 主功能选择always @(*) begincase(op)3'b000: out = add_result[WIDTH-1:0]; // 加法3'b001: out = sub_result[WIDTH-1:0]; // 减法3'b010: out = not_out;3'b011: out = and_out; // 与3'b100: out = or_out; // 或3'b101: out = xor_out; // 异或3'b110: out = { {(WIDTH-1){1'b0}}, signed_lt }; // 带符号比较3'b111: out = { {(WIDTH-1){1'b0}}, eq }; // 判等default: out = {WIDTH{1'b0}};endcaseend// 标志位生成assign zero = (out == {WIDTH{1'b0}});assign carry = (op == 3'b000) ? add_result[WIDTH] : (op == 3'b001) ? ~sub_result[WIDTH] : 1'b0;assign overflow = (op == 3'b000) ? ((a[WIDTH-1] == b[WIDTH-1]) && (add_result[WIDTH-1] != a[WIDTH-1])) :(op == 3'b001) ? ((a[WIDTH-1] != b[WIDTH-1]) && (sub_result[WIDTH-1] != a[WIDTH-1])) : 1'b0;endmodule// 七段译码器模块
module seg7_decoder (input [3:0] bin,output reg [7:0] seg // a-g + dp
);always @(*) begincase(bin)4'h0: seg = 8'b00000011; // 04'h1: seg = 8'b10011111; // 14'h2: seg = 8'b00100101; // 24'h3: seg = 8'b00001101; // 34'h4: seg = 8'b10011001; // 44'h5: seg = 8'b01001001; // 54'h6: seg = 8'b01000001; // 64'h7: seg = 8'b00011111; // 74'h8: seg = 8'b00000001; // 84'h9: seg = 8'b00001001; // 9default: seg = 8'b11111111; // 全灭endcaseend
endmodule
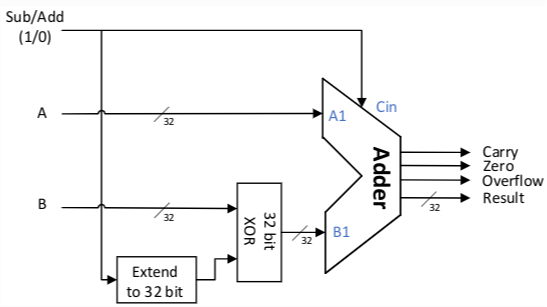 加法是数字系统中最常执行的运算,加法器是ALU(算术逻辑部件 Arithmetic-Logic Unit )的核心部件。 减法可以看作是被减数与取负后的减数进行加法。即用加法器同时实现加法和减法两种运算。乘法也可以利用移位相加的算法来实现。因此,加法器可以说是计算机中最“繁忙”的部件了。
加法是数字系统中最常执行的运算,加法器是ALU(算术逻辑部件 Arithmetic-Logic Unit )的核心部件。 减法可以看作是被减数与取负后的减数进行加法。即用加法器同时实现加法和减法两种运算。乘法也可以利用移位相加的算法来实现。因此,加法器可以说是计算机中最“繁忙”的部件了。:吉布斯不等式的证明)
![题解:AT_agc028_e [AGC028E] High Elements](http://pic.xiahunao.cn/题解:AT_agc028_e [AGC028E] High Elements)



![Luogu P10778 BZOJ3569 DZY Loves Chinese II 题解 [ 紫 ] [ Xor Hashing ] [ 线性基 ] [ DFS 树 ]](http://pic.xiahunao.cn/Luogu P10778 BZOJ3569 DZY Loves Chinese II 题解 [ 紫 ] [ Xor Hashing ] [ 线性基 ] [ DFS 树 ])






)
)


)
)

