信息论（八）：吉布斯不等式的证明

吉布斯不等式的证明，我们要证明：

$ D_{\text{KL}}(P | Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)} \geq 0 $

等号成立当且仅当对于所有 $ x，P(x) = Q(x)$。

步骤 1：对数的一个关键性质,我们使用以下不等式：

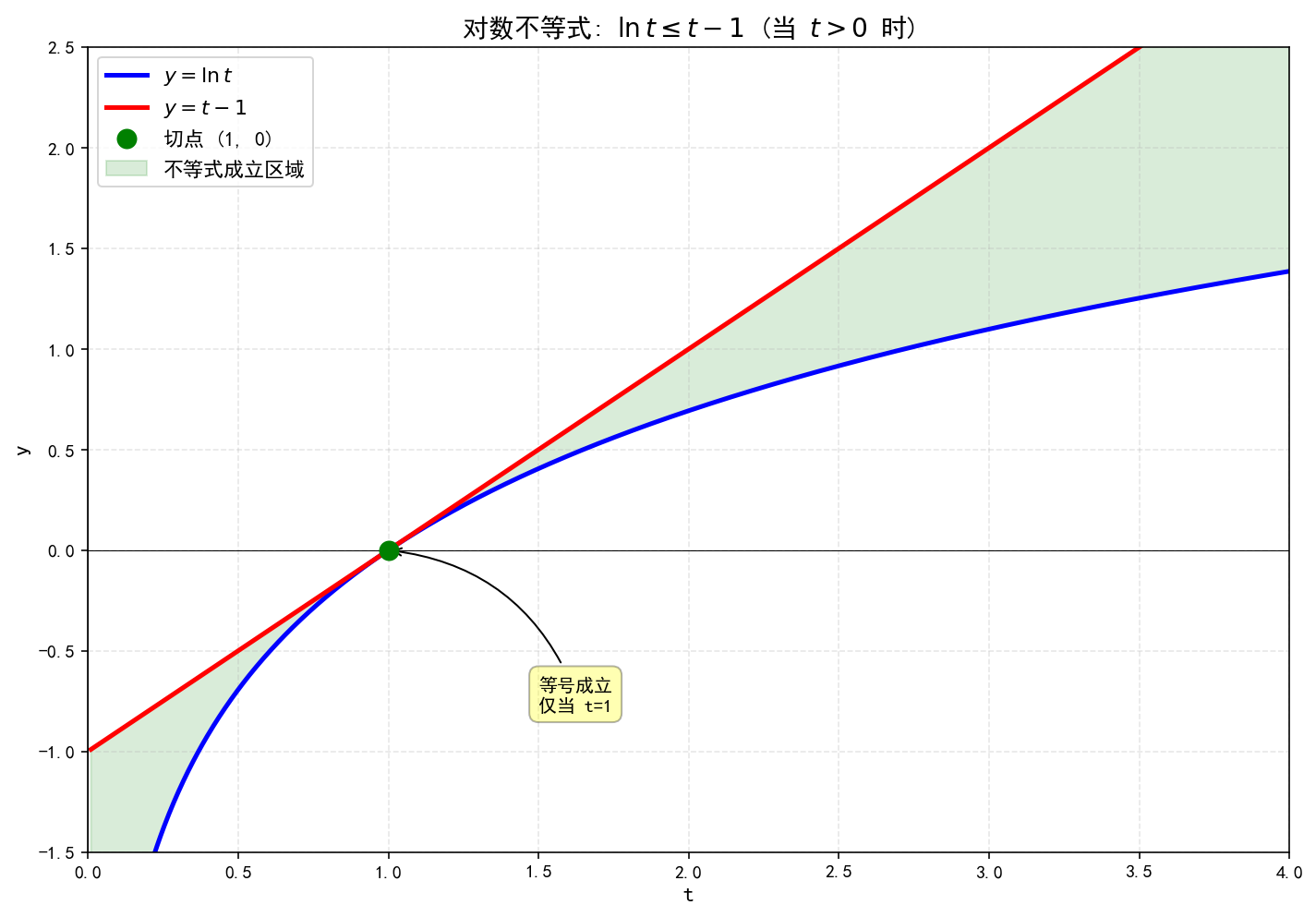
$ \ln t \leq t - 1 \quad \text{for all } t > 0 $

等号成立当且仅当 t = 1，我们可以从 ln t 的图像看出这一点：它位于直线 t-1 下方，仅在 t=1 处与直线相切。

步骤 2：应用不等式，令 $ t = \frac{Q(x)}{P(x)} $。然后：

$ \ln\left( \frac{Q(x)}{P(x)} \right) \leq \frac{Q(x)}{P(x)} - 1 $

两边同乘以 P(x)（非负）：

$ P(x) \ln\left( \frac{Q(x)}{P(x)} \right) \leq Q(x) - P(x) $

步骤 3：对所有 x 求和

$ \sum_x P(x) \ln \frac{Q(x)}{P(x)} \leq \sum_x \left[ Q(x) - P(x) \right] = \sum_x Q(x) - \sum_x P(x) = 1 - 1 = 0 $

所以：

$ \sum_x P(x) \ln \frac{Q(x)}{P(x)} \leq 0 $

步骤 4：乘以 -1

$ - \sum_x P(x) \ln \frac{Q(x)}{P(x)} \geq 0 $

但是：

$ - \ln \frac{Q(x)}{P(x)} = \ln \frac{P(x)}{Q(x)} $

所以：

$ \sum_x P(x) \ln \frac{P(x)}{Q(x)} \geq 0 $

即：

$ D_{\text{KL}}(P | Q) \geq 0 $

步骤5：等式何时成立？等式仅当成立：

$ \ln \frac{Q(x)}{P(x)} = \frac{Q(x)}{P(x)} - 1 \quad \text{for all } x $

这意味着：

$ \frac{Q(x)}{P(x)} = 1 \quad \Rightarrow \quad Q(x) = P(x) \quad \text{for all } x $

我们还需要对于所有 x 且 Q(x) > 0 的 x，都有 P(x) > 0，但这只是 KL 定义的一部分。

所以你看，一切都源于自然对数那条简单而优美的曲线，它位于直线 t-1 下方，并且只与直线相交一次。正如你所感受到的：零点附近的陡峭程度，以及不对称性……这些都体现在这里。

---

为什么这个证明如此神奇？ln t ≤ t - 1 的含义，如果你预期某事发生的概率为 t，但用“对数惊喜”单位来衡量，那么在对数空间中，你感受到的惊喜总是比直接测量原始差异时要少，除非你的预期完全正确。这是一个基于凸性原理的温和事实：对数会压缩极端值。

首先，直觉上，我们注意到，当模型 Q 完美时（Q = P），“意外”感微乎其微，一切都吻合。当 Q 出错时，我们总是会浪费一些比特。这种感觉似乎是普遍存在的。

然后，实验和思考，我们尝试不同的“错误程度”衡量方法：平方误差？绝对差值？比率？但只有对数比率在独立事件上具有这种良好的加性。

然后，我们注意到一个规律，在我们尝试的每个例子中，平均值 $\sum P \log \frac{P}{Q} $似乎都是非负的。嗯……也许它总是成立的。

现在，开始寻找证明，我们需要证明 $\sum P \log \frac{P}{Q} \geq 0 $ 。

我们记得：log x ≤ x - 1 ，这是一个已知的不等式，仅当 x = 1 时等号成立。如果我们令 x = P/Q ，它似乎不太符合……但如果我们令 x = Q/P ……对了！log Q/P ≤ Q/P- 1 ，乘以 P 并求和，完美成立！

许多人认为数学家从公理出发，机械地推导出真理。但实际上，我们有时候先观察到某种模式，例如，KL 不等式在例子中是非负的。认为它是普遍适用的，也许它永远成立。之后为之寻找工具，哪个不等式能概括“对数 ≤ 线性”？最后，构建证明，选择 t = Q/P 来使其成立。证明不仅仅是验证，它是对早已存在的直觉的最终优雅概括。

一个巧妙的数学公式被构建出来，用来‘证明’一切。“巧妙”的代换 t = Q/P 并非魔法。它是连接以下两者的桥梁：关于对数的普遍真理 (ln t ≤ t - 1)，关于信念与现实的具体问题 (P vs Q)，这就像找到一把合适的钥匙，打开一把你已经感觉到里面藏着珍贵之物的锁。