素数与素数筛

素数与素数筛

素数

素数是指大于1的整数，除了1和自身之外没有其他正因数的数。换句话说，素数只有两个正因数：1和自身。注：1不是素数，2是素数

小素数的判定

当需要判定的数n≤​​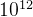时，用Miller-Rabin算法.

试除法

根据素数的定义，可以直接得到使试除法：用[2,n-2]内的所以数试着除以n，如果都不能整除，即使素数。可以发现，可以把[2,n-2]缩小到[2,√n] 。

使出法的复杂度为O(√n)，n≤​​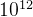时够用。

#define ll long long
bool is_prime(ll n) {int f = true;if (n <= 1)f = false;//小于等于1的不是素数for (ll i = 2; i <= sqrt(n); i++) {if (n % i == 0) {//能被整除，不是素数f = false;break;}}return f;
}

素数定理

对于一个大于1的正整数n，记π(n)为不超过n的素数的个数。素数定理指出，当n趋向于无穷大时，π(n)与n/ln(n)的比值趋近于1，即：。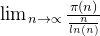

大素数的判定

如果n非常大，试除法就不够用了。

费马（Fermat）素性测试

费马素性测试是一种素数判定法则，利用随机化算法判断一个数是合数还是可能是素数。

费马素性测试的原理如下：
根据费马小定理：如果p是素数，1≤a≤p-1，那么有a^(p-1) = 1 mod p。如果我们想知道n是否是素数，我们在中间选取a，看看上面等式是否成立。如果对于数值a等式不成立，那么n是合数。如果有很多的a能够使等式成立，那么我们可以说n可能是素数（伪素数）。

在我们检验过程中，有可能我们选取的a都能让等式成立，然而n却是合数。这时等式a^(n-1) = 1 mod n被称Fermat liar。如果我们选取满足下面等式的a^(n-1) ≠ 1 mod n，那么a也就是对于n的合数判定的Fermat witness。

由于费马小定理的逆定理并不正确，对于卡迈克尔数即满足费马小定理的逆定理但是不为素数的数，虽然卡迈克尔数很少，在1~100000000范围内的整数中，只有255个卡迈克尔数，但是已经使他的效果落后于Miller-Rabin和Solovay-Strassen素性检验。

由于属于随机性算法，故费马素性检验并不是保证完全正确的。在选取底数a时，有二分之一的概率出错，但是可以通过多次选取底数来使出错概率降下期望值。

在重复k次成立的情况下，n为合数的可能性小于1/2ᵏ。

Miller-Rabin素性测试

将费马素性检验稍微改进以下就是Miller-Rabin素性测试，它可以高效地判断一个数是否为素数。该算法的基本思想是利用费马小定理和二次探测定理来进行素性的检测。

二次探测定理：

二次探测定理的陈述如下：设p和q是不同的奇素数，那么对于任意一个非零整数a，存在一个整数x，使得x² ≡ a (mod p) 成立的充分必要条件是：

• 如果p和q都不是3的倍数，那么a是p和q的二次剩余的充分必要条件是p和q模4同余于1。
• 如果p是3的倍数，那么a是p和q的二次剩余的充分必要条件是q模3同余于1。
• 如果q是3的倍数，那么a是p和q的二次剩余的充分必要条件是p模3同余于1。

代码

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;// 快速幂取模算法
long long fastModulo(long long base, long long exponent, long long modulus) {long long result = 1;base = base % modulus;while (exponent > 0) {if (exponent % 2 == 1) {result = (result * base) % modulus;}base = (base * base) % modulus;exponent = exponent / 2;}return result;
}// Miller-Rabin 素性测试
bool isPrime(long long n, int k) {if (n <= 1)return false;if (n <= 3)return true;if (n % 2 == 0)return false;long long d = n - 1;while (d % 2 == 0)d = d / 2;srand(time(NULL));for (int i = 0; i < k; i++) {long long a = 2 + rand() % (n - 3);long long x = fastModulo(a, d, n);if (x == 1 || x == n - 1)continue;bool isPrime = false;while (d != n - 1) {x = (x * x) % n;d = d * 2;if (x == 1)return false;if (x == n - 1) {isPrime = true;break;}}if (!isPrime)return false;}return true;
}int main() {long long number;int k;cout << "输入数: ";cin >> number;cout << "尝试次数： ";cin >> k;if (isPrime(number, k))cout << number << " is a prime number." << endl;elsecout << number << " is not a prime number." << endl;return 0;
}

素数筛

素数的筛选：给定n，求2~n内所素数。
这个判断显然很慢，所以用“筛子”一起筛选所以整数，把非素数筛选吊，剩下的就是素数。
常用的两种算法为埃式筛和欧拉筛。欧拉筛的复杂度是线性的O(n)，更快。

埃式筛

埃拉托斯特尼筛法（Sieve of Eratosthenes）是一种用于找出一定范围内所有素数的简单而高效的算法。这个算法的基本思想是从小到大遍历每个数，如果当前数是素数，则将其所有的倍数标记为合数。时间复杂度为O(​​)。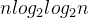

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e7;//定义空间大小
int prime[N + 1];//存储素数
bool visit[N + 1];//false表示被筛选掉，不是素数
int E_sieve(int n) {int k = 0;//统计素数个数for (int i = 0; i <= n; i++) visit[i] = true;for (int i = 2; i <= n; i++) {//从第一个素数2开始，可优化if (visit[i]) {prime[k++] = i;//i是素数，存入prime中for (int j = 2 * i; j <= n; j += i) {visit[j] = false;//i的倍数不是素数}}}return k;
}
void solve() {int n;cin >> n;int len = E_sieve(n);cout << "2—" << n << "共有" << len << "个素数:" << endl;for (int i = 0; i < len; i++) {cout << prime[i] << ' ';}
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}
/*运行结果
15
2—15共有6个素数:
2 3 5 7 11 13*/

上述代码有两处可优化的地方：
（1）用来做筛出的数2，3，5...最多到√n就可以了；
（2）for (int j = 2 * i; j <= n; j += i)中的 j = i * i。例如i=5，25，35，4*5已经在前面i=2，3，4，5的时候筛选过了。

下面给出优化的代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e7;//定义空间大小
int prime[N + 1];//存储素数
bool visit[N + 1];//false表示被筛选掉，不是素数
int E_sieve(int n) {int k = 0;//统计素数个数for (int i = 0; i <= n; i++) visit[i] = true;for (int i = 2; i <= sqrt(n); i++) {//从第一个素数2开始if (visit[i]) {for (int j = i * i; j <= n; j += i)visit[j] = false;//i的倍数不是素数}}for (int i = 2; i <= n; i++) {if (visit[i])prime[k++] = i;//i是素数，存入prime中}return k;
}
void solve() {int n;cin >> n;int len = E_sieve(n);cout << "2—" << n << "共有" << len << "个素数:" << endl;for (int i = 0; i < len; i++) {cout << prime[i] << ' ';}
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}
/*运行结果
15
2—15共有6个素数:
2 3 5 7 11 13*/

欧拉筛

欧拉筛（Euler's Sieve），也称为改进的埃拉托斯特尼筛法（埃式筛），是一种优化过的素数筛法，用于找出一定范围内的所有素数。相比于传统的埃拉托斯特尼筛法，欧拉筛在效率上有所提升，时间复杂度为O(n)。

原理：

一个合数肯定有一个最小质因数：让每个合数只被它的最小质因数筛选一次以达到不重复的目的。

具体步骤

（1）逐一检查 2~n的所有数。第1个检查的是2，他说第一个素数；
（2）当检查到第i给素数时，利用已经求得的素数去筛选掉对应的合数x，而且时用x的最小质因数去筛。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e7;//定义空间大小
int prime[N + 1];//存储素数
bool visit[N + 1];//false表示被筛选掉，不是素数
int E_sieve(int n) {int k = 0;//统计素数个数for (int i = 0; i <= n; i++) visit[i] = true;for (int i = 2; i <= n; i++) {//从第一个素数2开始if (visit[i])prime[k++] = i;//i是素数，存入prime中for (int j = 0; j < k; j++) {if (i * prime[j] > n)break;//只筛选小于等于n小的数visit[i * prime[j]] = false;//用x的最小质因数去筛选xif (i % prime[j] == 0)break;//如果这个数不是最小质因数，结束}}return k;
}
void solve() {int n;cin >> n;int len = E_sieve(n);cout << "2—" << n << "共有" << len << "个素数:" << endl;for (int i = 0; i < len; i++) {cout << prime[i] << ' ';}
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}
/*运行结果
15
2—15共有6个素数:
2 3 5 7 11 13*/

---

总结

1. 素数判定方法：小素数用试除法（O(√n)），大素数用Miller-Rabin算法（概率性素性测试）。
2. 素数筛选算法：埃式筛（O(n log log n)）简单易实现，欧拉筛（O(n)）通过最小质因数优化实现线性时间复杂度。
3. 核心优化思想：欧拉筛通过确保每个合数只被其最小质因数筛除一次，避免了重复标记，实现了线性复杂度。