模拟赛 43

感觉质量终于变高了，题也变难了。

T1

题面

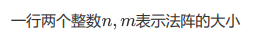
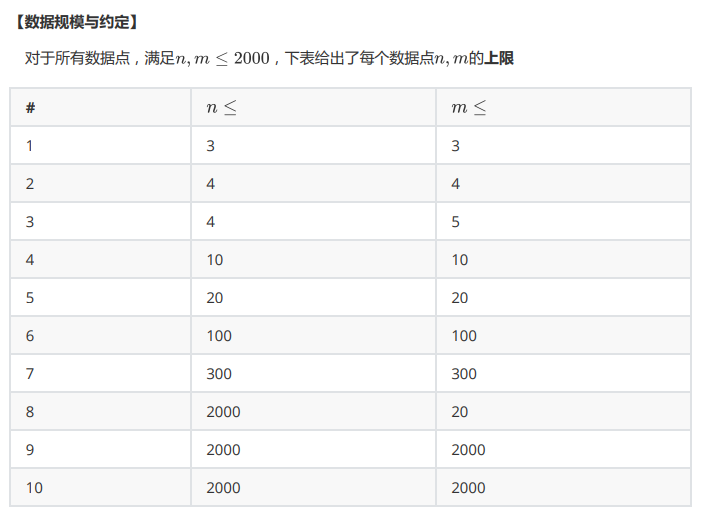
原题竟然是 3100，和一位。不难发现最后 \(0\) 和 \(1\) 的连通块数量必须在 \([1,2]\) 之间，且要有至少一个大于 \(1\)。先讨论 \(1\) 的连通块数量为 \([1,2]\)，\(0\) 的连通块数量为 \(1\) 的情况，如图所示：

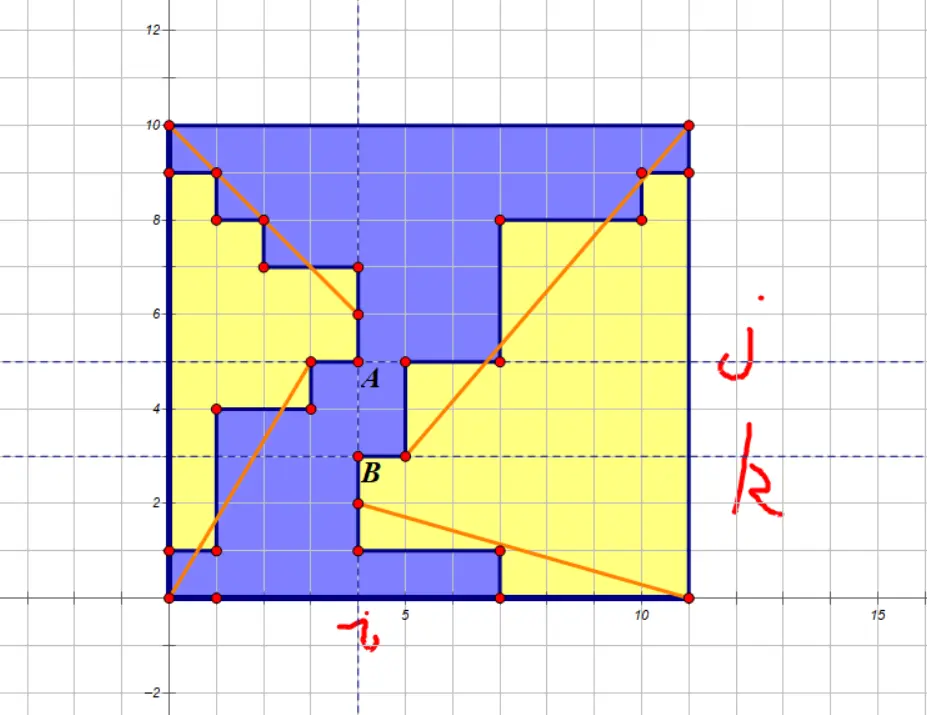
\(2\) 个连通块一个全部在 \(i\) 左侧，另一个全部在 \(i\) 右侧；设左侧的连通块最右列的 \(0\) 区间是 \([l_1,r_1]\)，左侧连通块的区间是 \([l_2,r_2]\)。记 \(j=r_1,k=l_2\)，显然必须满足 \(j\le k\)（取等的时候 \(1\) 的连通块数量为 \(2\)）。考虑得到 \(i,j,k\) 后如何计算方案数，左上角的递增序列可以视为从 \((1,1)\) 每次向右/下走一步走到 \((i,j)\) 的方案数，但是由于点 \(A\) 是区间的下端点，所以最后一步必须向下走，所以视为走到 \((i-1,j)\) 的方案数。方案数易求。其它 \(3\) 处同理。暴力计算是 \(O(n^2m)\) 的，使用前缀和优化到 \(O(nm)\)。

另一大类情况是类似的，只要把 \(n,m\) 交换就可以算出来了。但是注意不要把两个连通块数量都为 \(2\) 的情况又算一遍。

T2

题面

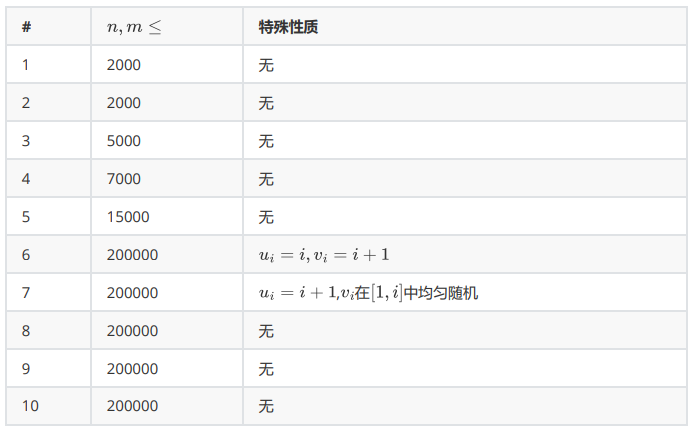
首先有结论：一棵树内离节点 \(x\) 最远的点必然是任意直径的某个端点。于是直接时光倒流，处理出每个树的任意直径的端点，加边时直接枚举所有 \(4\) 个端点的组合情况取最大值即可。

点击查看代码

#include<bits/stdc++.h>
#define int long long
#define MAXN 400005
using namespace std;
const int inf=1e18;
int n,m,ans[MAXN],cnt,head[MAXN],deep[MAXN],fa[MAXN][22],r[MAXN],qcnt,d[MAXN][2];
struct Edge{int value,next;
}edge[MAXN*2];
void addedge(int u,int v){edge[++cnt].value=v;edge[cnt].next=head[u];head[u]=cnt;
}
struct E{int u,v,b;
}e[MAXN];
struct Node{int opt,t,id,x;
}a[MAXN];
bool cmp(Node x,Node y){return x.t>y.t;
}
void dfs(int x,int fat){fa[x][0]=fat;deep[x]=deep[fat]+1;for(int i=1;i<=20;i++)fa[x][i]=fa[fa[x][i-1]][i-1];for(int i=head[x];i;i=edge[i].next){int y=edge[i].value;if(y!=fat)dfs(y,x);}
}
int LCA(int x,int y){if(deep[x]<deep[y])swap(x,y);for(int i=20;i>=0;i--){if(deep[fa[x][i]]>=deep[y])x=fa[x][i];}if(x==y)return x;for(int i=20;i>=0;i--){if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];}return fa[x][0];
}
int dis(int x,int y){int l=LCA(x,y);return deep[x]+deep[y]-deep[l]*2;
}
int find(int x){if(r[x]!=x)r[x]=find(r[x]);return r[x];
}
struct Tmp{int x,y;
}t[10];
bool cmpt(Tmp x,Tmp y){return dis(x.x,x.y)>dis(y.x,y.y);
}
void merge(int x,int y){//cout<<x<<' '<<y<<"\n";x=find(x),y=find(y);t[1]=(Tmp){d[x][0],d[x][1]};t[2]=(Tmp){d[x][0],d[y][0]};t[3]=(Tmp){d[x][0],d[y][1]};t[4]=(Tmp){d[x][1],d[y][0]};t[5]=(Tmp){d[x][1],d[y][1]};t[6]=(Tmp){d[y][0],d[y][1]};sort(t+1,t+7,cmpt);d[y][0]=t[1].x,d[y][1]=t[1].y;//cout<<d[y][0]<<' '<<d[y][1]<<"\n";r[x]=y;
}
int que(int x){int y=find(x);return max(dis(x,d[y][0]),dis(x,d[y][1]));
}
signed main(){freopen("block.in","r",stdin);freopen("block.out","w",stdout);scanf("%lld%lld",&n,&m);for(int i=1;i<n;i++){scanf("%lld%lld",&e[i].u,&e[i].v);addedge(e[i].u,e[i].v);addedge(e[i].v,e[i].u);}dfs(1,0);for(int i=1;i<=n;i++)r[i]=i,d[i][0]=d[i][1]=i;for(int i=1;i<=m;i++){scanf("%lld%lld",&a[i].opt,&a[i].x);a[i].t=i;if(a[i].opt==2)a[i].id=++qcnt;else e[a[i].x].b=1;}for(int i=1;i<n;i++){if(!e[i].b){merge(e[i].u,e[i].v);}}sort(a+1,a+m+1,cmp);for(int i=1;i<=m;i++){if(a[i].opt==1){merge(e[a[i].x].u,e[a[i].x].v);}else{ans[a[i].id]=que(a[i].x);}}for(int i=1;i<=qcnt;i++){printf("%lld\n",ans[i]);}return 0;
}

T3