简介
三分图染色指对于一个图进行三种颜色的染色,每条边的两个端点颜色不同
本文旨解决 m-n$\le$7的染色问题,即边数只比点数多7
做法
考虑对于每个度数$\ge$3的结点作暴力dfs染色,
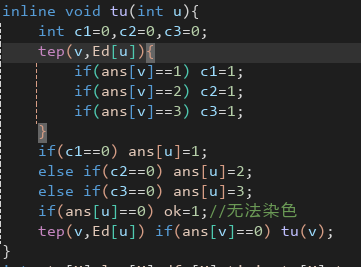
代码差不多就是这样的
即能染颜色1就染颜色1,能染颜色2就染颜色2,能染颜色3就染颜色3.
出发点的选择
发现当一个结点染色失败时需要至少三条边与其相连,而如果图上只有一个度数大于等于三的点,
直接从这个点出发一定可以直接暴力染完所有度数为1,2的点
考虑分析有两个度数为三的点要相互染色失败
染色
考虑当一个度数为三的节点暴力染色失败后的样子:
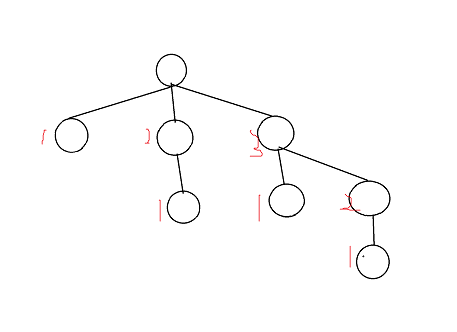
最上方的点无法染色,因为下方的三个点已经被被迫染上了三种颜色,
下方的结点一定染色成1,2,3,那么再下方的结点一定会把1,2的位置填满
由于bfs暴力染色所以考虑先访问该点下方1,2,3,最后访问无法染色的结点,所以需要返祖边
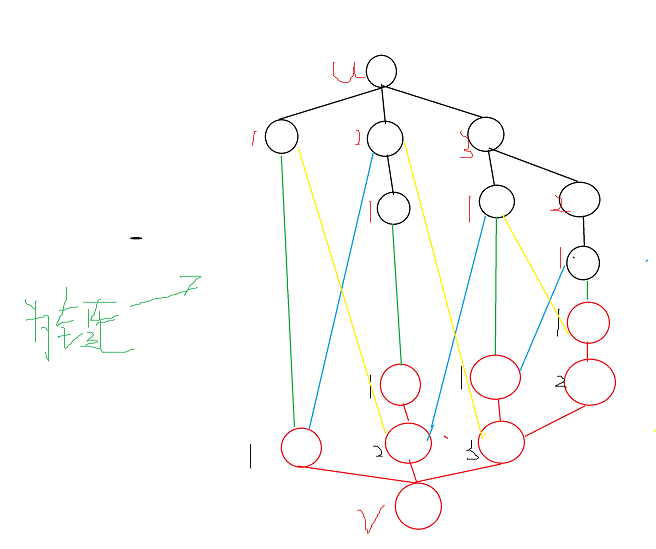
中间的绿色为本来连通图的链接边
由于要返祖,所以向下后需要退回到另一条链上,上下的u,v有四条关键边,所以上下分别需要6条返祖边
6条返祖边会出现12个度数为三的点,加上原来要形成

结构需要两个三度点
所以形成一对互相染色失败的点共需要2+2+12个三度点,16个三度点在m-n=7时存在一个,当m-n=7时最多16个三度点
但是不是所有的三度点都会失败,因为共有16个
所以直接把所有度数为三的点暴力向下染色,当有正确答案时一定可以找到正确的答案









 - 实践)









