二维前缀和与二维差分数组

二维前缀和

定义

给定一个m行n列的矩阵，它的前缀和sum[i][j]定义为前i行中前i列所有区域格子元素的累加和， 即\(sum[i+1][j+1] = \sum\limits_{row=0, col=0}^{i, j} matrix[row][col]\)， 由定义易得二维前缀和的递推公式为 sum[i + 1][j + 1] = matrix[i][j] + sum[i][j + 1] + sum[i + 1][j] - sum[i][j]。

假设查询区域为左上角(r1, c1)到右下角(r2, c2)范围内元素的累加和， 借助二维前缀和同样可以将单次查询时间复杂度降低到O(1)， 计算公式为 sum[r2 + 1][c2 + 1] - sum[r2 + 1][c1] - sum[r1][c2 + 1] + sum[r1][c1]， 下图是对该公式的直观解释：

代码示例

可直接在 【LeetCode 304】二维区域和检索 - 矩阵不可变 执行提交测试：

class NumMatrix {private int[][] sum;public NumMatrix(int[][] matrix) {int m = matrix.length, n = matrix[0].length;sum = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sum[i + 1][j + 1] = matrix[i][j] + sum[i][j + 1] + sum[i + 1][j] - sum[i][j];}}}public int sumRegion(int row1, int col1, int row2, int col2) {return sum[row2 + 1][col2 + 1] - sum[row2 + 1][col1] - sum[row1][col2 + 1] + sum[row1][col1];}
}

二维差分数组

引言

延续一维前缀和与差分数组的关联思想， 为了将二维数组的区域修改借助差分实现单次操作仅需O(1)时间复杂度， 同样需要借助二维差分数组。

与原始二维数组的互相转换

由于最终差分数组是通过计算前缀和来得到原数组， 所以从前缀和递推公式 sum[i + 1][j + 1] = matrix[i][j] + sum[i][j + 1] + sum[i + 1][j] - sum[i][j] 来反推， 由原数组初始化差分数组的递推公式为 diff[i][j] = matrix[i + 1][j + 1] - matrix[i][j + 1] - matrix[i + 1][j] + matrix[i][j]， 同样为了方便处理首行首列数据通常二维差分也会在首行首列前预添加全为0的格子， 以下是二维差分与原始数组互相转换的代码示例:

   private int[][] init(int[][] matrix) {int m = matrix.length, n = matrix[0].length;// 实际应用中为了后续修改和最终求前缀和方便, 差分数组首末行列都会各添加一行/列int[][] diff = new int[m + 2][n + 2];for (int i = 0; i < m; i++) {diff[i + 1][1] = matrix[i][0];}for (int j = 0; j < n; j++) {diff[1][j + 1] = matrix[0][j];}for (int i = 1; i < m; j++) {for (int j = 1; j < n; j++) {diff[i + 1][j + 1] = matrix[i][j] - matrix[i - 1][j] - matrix[i][j - 1] + matrix[i - 1][j - 1]; }}return diff;}private int[][] convert(int[][] diff) {int m = diff.length - 2, n = diff[0].length - 2;int[][] sum = new int[m][n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {diff[i + 1][j + 1] += diff[i][j + 1] + diff[i + 1][j] - diff[i][j];sum[i][j] = diff[i + 1][j + 1];}}return sum;}

批量修改二维区域与差分数组的关系

假设要求将二维数组从左上角(r1, c1)到右下角(r2, c2)区域的元素值统一增加， 只要借助更新常数个差分数组中的元素值就能实现， 结合下图来解释具体对应哪几个下标元素以及为什么：

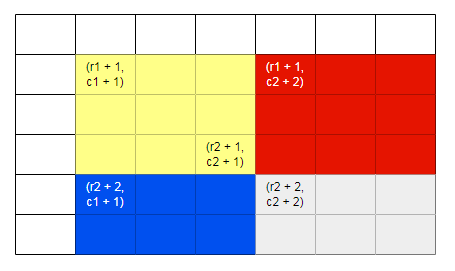
1. 黄红蓝灰四色区域代表的前缀和受影响范围是由左上角格子(r1 + 1, c1 + 1)， 也就是对应差分数组中diff[r1 + 1][c1 + 1] += val；
2. 排除红+灰区域代表的前缀和不受影响， 对应差分数组中diff[r1 + 1][c2 + 2] -= val；
3. 同理排除蓝+灰区域不受影响是对应diff[r2 + 2][c1 + 1] -= val；
4. 两次排除时灰色区域操作了两次需要再回撤一次， 对应再将diff[r2 + 2][c2 + 2] += val；
5. 最终通过更新4个差分数组中的元素达到仅影响其前缀和范围中黄色部分的目的， 也就是对原数组中指定区域统一增加了val。

代码示例如下：

   private void add(int[][] diff, int r1, int c1, int r2, int c2, int val) {diff[r1 + 1][c1 + 1] += val;diff[r1 + 1][c2 + 2] -= val;diff[r2 + 2][c1 + 1] -= val;diff[r2 + 2][c2 + 2] -= val;}

相关题目

【题集】前缀和与差分数组

写在最后

二维差分不太好单独理解， 但是结合二维前缀和以及画图就比较清晰易懂了， 代码实现时根据个人习惯来决定是否要预添加全为0的行/列避免下标越界判断。 这次也是前几天每日一题中有用到而且被下标对应关系绕的有点晕才想起来整理相关内容， 本内容目前仅限于自己由一维前缀和与差分的关系延伸学习理解的总结， 后续有空再结合 B站左神相关视频 继续学习看有没有缺漏。