为什么要使用immer库?
-
首先从不使用 Immer 的情况下,useState 是如何更新状态的,来开始解释
useState 的更新方式有两种:
方式1:直接设置新值
const [count, setCount] = useState(0); setCount(5); // 直接设置新值
方式2:基于前一个状态计算新值
const [count, setCount] = useState(0); setCount(prevCount => prevCount + 1); // 基于前一个状态关键点: 对于对象和数组,我们必须返回一个新的引用,React 才能检测到变化。
-
不使用 Immer 的状态更新的具体示例:
示例一:简单对象更新
![image]()
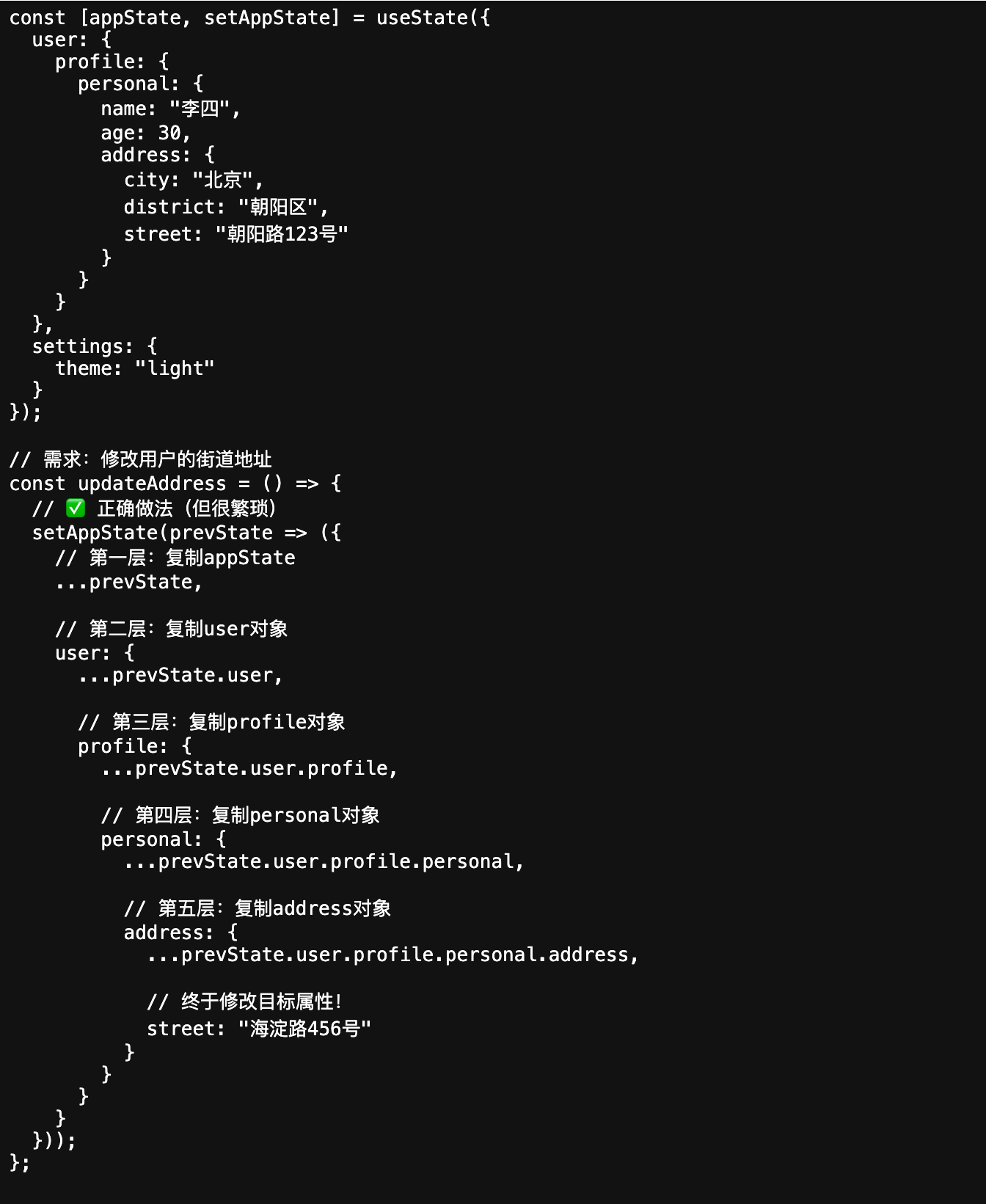
示例二:嵌套对象更新(痛点所在!)
![image]()
看到了吗? 为了修改一个深层的属性,我们需要写很多展开操作符(...),层层复制!
示例三:数组更新
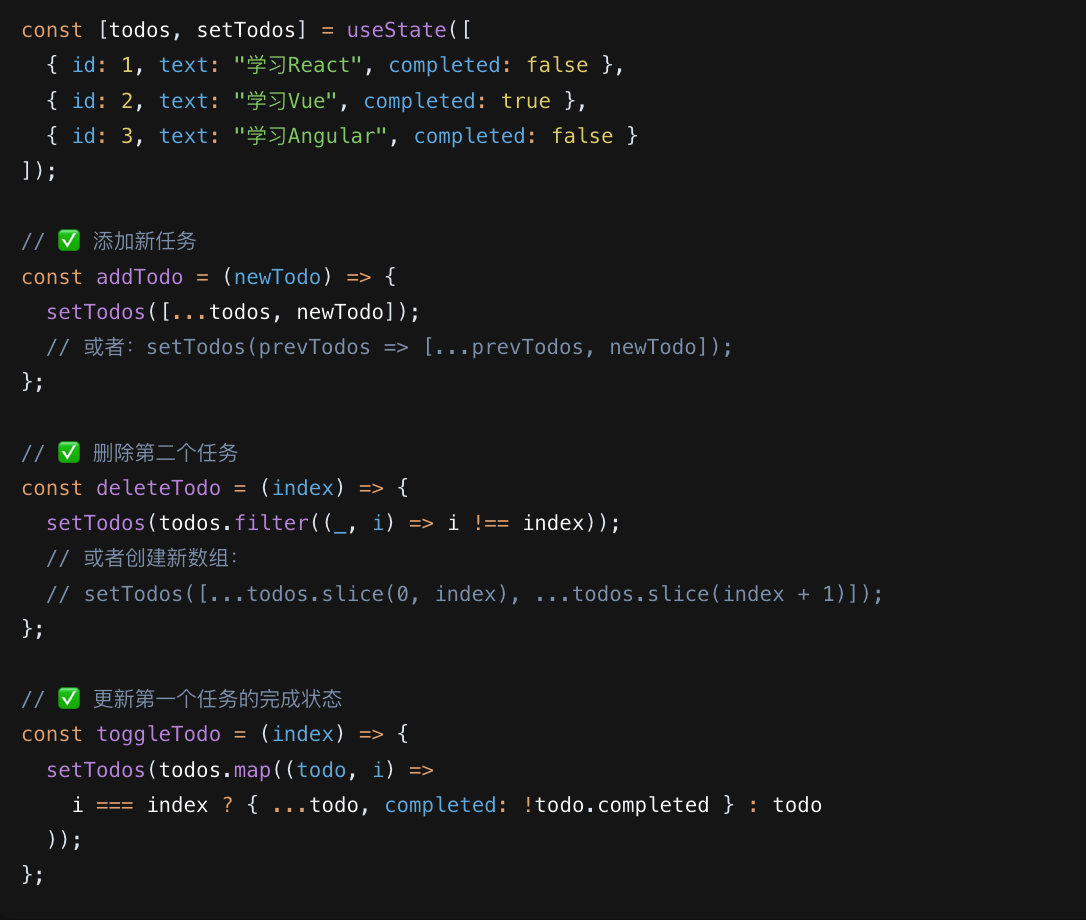
- 使用 Immer 的写法
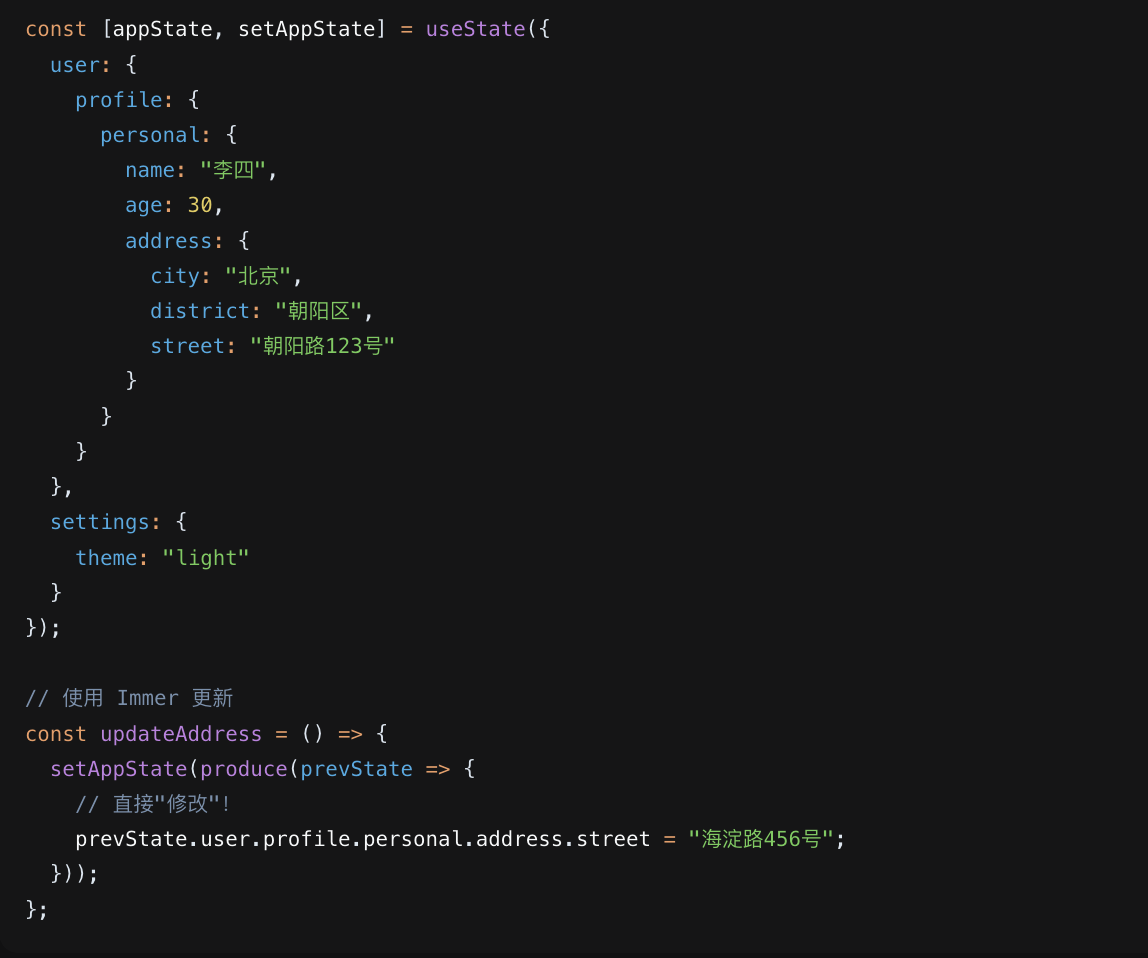
示例一:同样的嵌套对象更新
![image]()
示例二:同样的数组操作
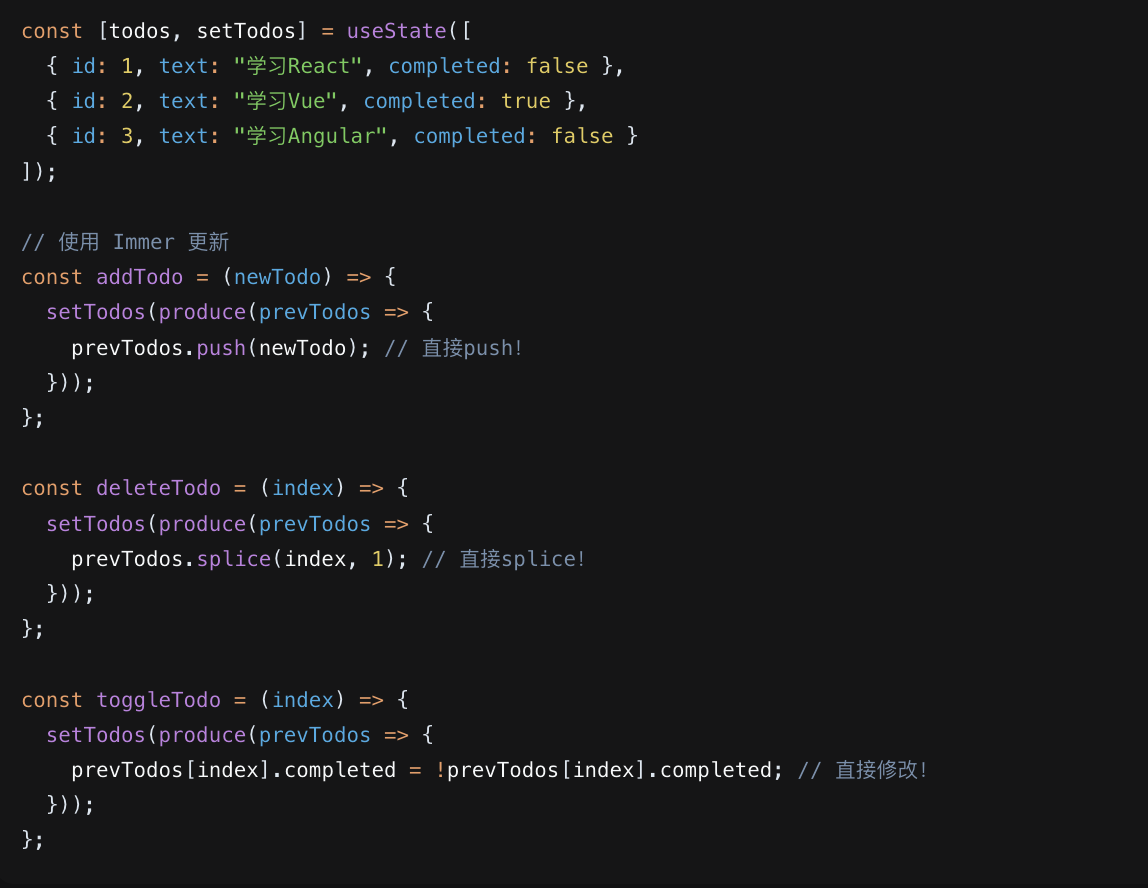
- 为什么 React 要求不可变更新?
4.1 检测数据的变化的(react使用引用对比来快速判断数据是否发生变化)
4.2 直接修改数据,引用就不会变化,react 就检测不到数据变化,也就不会触发重新渲染
4.3 正确的方式应该创建一个新的引用,如setState({ ...state, count: 1 });// 创建了新对象,引用变了 // React认为:"引用变了,数据变了,重新渲染!"
**总结: **
不使用immer时:
* 必须手动创建新数据/新对象
* 使用展开运算符 (...)/ map / filter / slice 等方法
* 深层次嵌套时变得冗余复杂
* 容易出错(忘记展开某一层)
使用immer时:
* 直接用可变的语法写代码
* immer在背后帮你处理所有不可变的细节
* 代码简洁直观,不容易出错
* 特别适合复杂的嵌套状态更新
简单说:Immer 不是 React 的必需品,而是让状态更新变得更加简单的语法糖,它让你在写代码修改复杂状态变化的时候,像是直接在修改状态,但实际上它帮你完成了所有不可变更的工作。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/962541.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!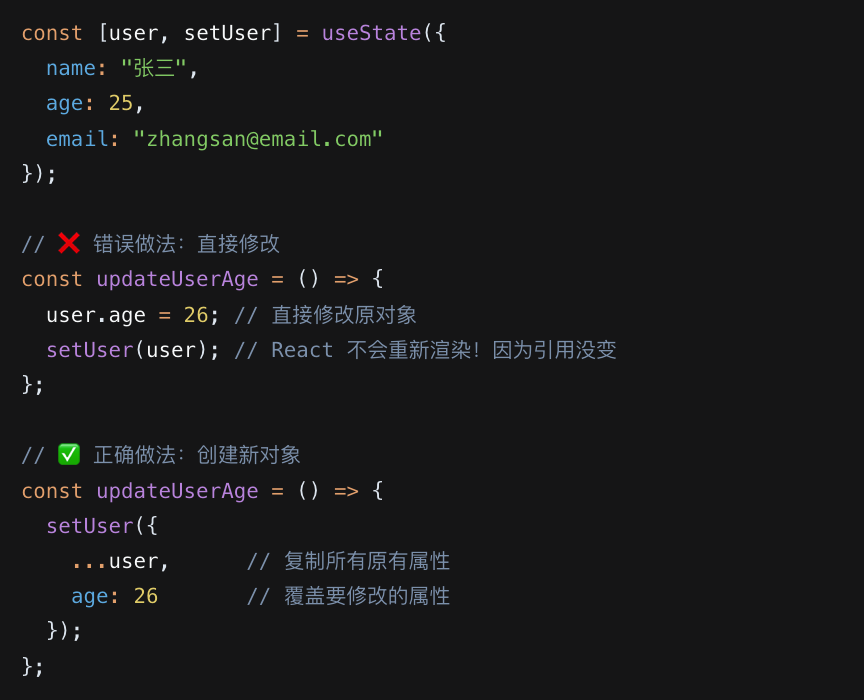


)
:揭秘ObjectSense的0“AI护城河”——微语言)










)




![P4784 [BalticOI 2016] 城市 (Day2) 小结](http://pic.xiahunao.cn/P4784 [BalticOI 2016] 城市 (Day2) 小结)