T1. P14460 寻雾启示
考虑 DP。令 \(f_i\) 为到达位置 \(i\) 的最短时间。
转移时,考虑枚举最后一个折返点 \(j\)。即:
- 先从 \(0\) 经过一系列步骤到 \(j\)。
- 从 \(j\) 折返到 \(0\),一直等待到铁锭足够。
- 先跑步到 \(j\),再铺路到 \(i\)。
\(j=0\) 即为不折返。
则有转移:
\[f_i=\min_{j=0}^{i-1} \max(ik,f_j+jt_2)+jt_2+(i-j)t_1
\]
\(O(n^2)\) DP 可以获得 \(90\rm pts\),出题人好温柔。
考虑进一步优化。发现把 \(j\) 相关项丢到 \(\max\) 里面,其左右式均为关于 \(j\) 的一次函数。
所以可能的转移点只可能在 \(0\)、\(i-1\)、以及交点左右侧的位置取到。
求交点能 \(O(1)\) 做。代码是 \(O(\log m)\) 二分求的,因为方便点。
时间复杂度 \(O(m)\) 或 \(O(m\log m)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define cal(x) (max(i*k,f[x]+(x)*t2)+(x)*t2+(i-(x))*t1)
using namespace std;
const int M=1e5+5,inf=1e15;
int t,m,k,t1,t2,f[M];//t1搭路 t2跑步
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>t;while(t--){cin>>m>>k>>t1>>t2;for(int i=1;i<=m;i++){int l=0,r=i-1;while(l<r){int mid=(l+r)>>1;if(f[mid]+mid*t2>=i*k) r=mid;else l=mid+1;}f[i]=min({cal(0),cal(l),cal(i-1)});if(l-1>=0) f[i]=min(f[i],cal(l-1));}for(int i=1;i<=m;i++) cout<<f[i]<<" ";cout<<"\n";}return 0;
}
T2. P14461 青年晚报
赛时无脑找规律的做法,没写证明,可以看洛谷题解区。
考虑贡献是可加的,一个很常见的技巧就是分别考虑 \(F,G\) 中的每一位对答案的贡献。
我们先考虑 \(n\) 为偶数的情况,此时 \(F_0\) 只能影响到 \(F_n\),\(G_0\) 只能影响到 \(G_n\)。
拿 \(F\) 举例,\(G\) 完全相同。打表可以发现,初始状态的一个 \(1\) 对之后的贡献如下(奇数行省去了,因为全为 \(0\)):
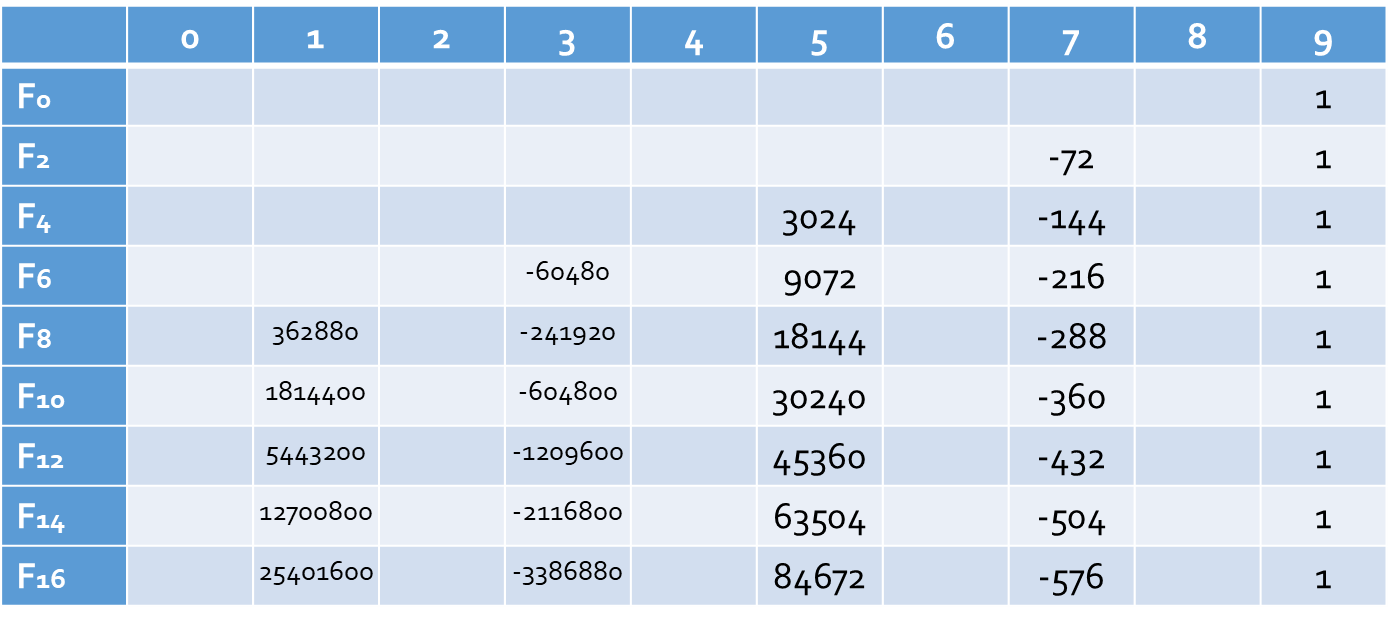
找一找规律:
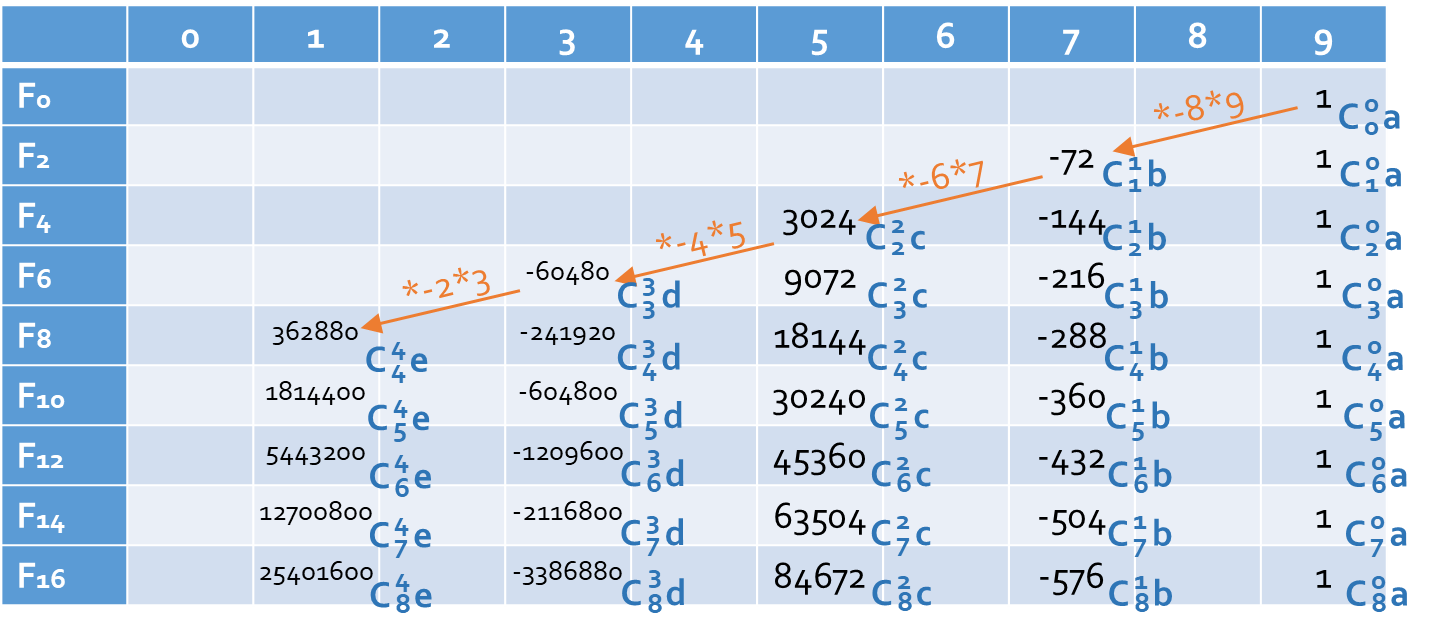
最后一行的组合数下标恒为 \(\dfrac{n}{2}\),可以 \(O(m)\) 地递推,而不需要 \(O(n)\)(赛时因为没想到这个丢了 \(8\rm{pts}\))。
如果 \(n\) 是奇数,就暴力再递推一轮即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=5005,P=1e9+7,speN=1e7+2;
int n,m,f[M],g[M],ff[M],gg[M],tf[M],tg[M],t[M];
int fc[speN],iv[speN];
inline int qp(int x,int n){int a=1;while(n){if(n&1) a=a*x%P;x=x*x%P,n>>=1;}return a;
}
inline int C(int n,int m){return fc[n]*iv[m]%P*iv[n-m]%P;}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);fc[0]=1;for(int i=1;i<speN;i++) fc[i]=fc[i-1]*i%P;iv[speN-1]=qp(fc[speN-1],P-2);for(int i=speN-2;~i;i--) iv[i]=iv[i+1]*(i+1)%P;cin>>n>>m;for(int i=0;i<=m;i++) cin>>f[i];for(int i=0;i<=m;i++) cin>>g[i];for(int i=0;i<=m;i++){if(!f[i]) continue;for(int j=i,r=0,fac=f[i]%P;j>=0;j-=2,r+=2){if(r>n) break;(ff[j]+=fac*C(n/2,(i-j)/2))%=P;(fac*=-(j-1)*j)%=P;}}for(int i=0;i<=m;i++){if(!g[i]) continue;for(int j=i,r=0,fac=g[i]%P;j>=0;j-=2,r+=2){if(r>n) break;(gg[j]+=fac*C(n/2,(i-j)/2))%=P;(fac*=-(j-1)*j)%=P;}}if(n&1){//再模拟一轮 for(int i=0;i<m;i++) tf[i]=(ff[i+1]*(i+1))%P,tg[i]=(gg[i+1]*(i+1))%P;for(int i=0;i<=m;i++) t[i]=(gg[i]+tg[i])%P,gg[i]=(ff[i]-tf[i])%P;for(int i=0;i<=m;i++) ff[i]=t[i];}for(int i=0;i<=m;i++) cout<<(ff[i]%P+P)%P<<" ";cout<<"\n";for(int i=0;i<=m;i++) cout<<(gg[i]%P+P)%P<<" ";return 0;
}


















)
