替换法解方程5例

(x²+x+1)²=x²(3x²+x+1)

令k=x²+x+1则(k-2x²)(k+x²)=0

>>> e=(x2+x+1)**2-x2*(3*x2+x+1)
>>> solve(e)
[-1/4 - sqrt(7)*I/4, -1/4 + sqrt(7)*I/4, 1/2 - sqrt(5)/2, 1/2 + sqrt(5)/2]

---

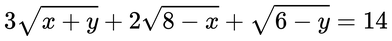
令k=√(x+y), m=√(8-x), n=√(6-y)
k²+m²+n²=14 〔重要〕
3k+2m+n=k²+m²+n²
k²+m²+n²-3k-2m-n=0
2k²+2m²+2n²-6k-4m-2n=0
(k-3)²+(m-2)²+(n-1)²=0

>>> e=3*sqrt(x+y)+2*sqrt(8-x)+sqrt(6-y)-14
>>> solve(e)
[{x: -122*y/169 - 140*sqrt(6 - y)/169 - 12*sqrt(14)*sqrt(-y**2 - 30*y*sqrt(6 - y) + 265*y + 600*sqrt(6 - y) - 1750)/169 + 1426/169}, {x: -122*y/169 - 140*sqrt(6 - y)/169 + 12*sqrt(14)*sqrt(-y**2 - 30*y*sqrt(6 - y) + 265*y + 600*sqrt(6 - y) - 1750)/169 + 1426/169}]

---

令x=√(m+1)，y=√(m-1)
(x+y)²=2m+2xy
2(x+y-xy)=(x+y)² - 2xy
2(x+y)=(x+y)²

>>> e=sqrt(m+1)+sqrt(m-1)-sqrt(m2-1)-m
>>> solve(e)
[5/4]

---

(2x³+x-3)³=3-x³

令2x³-3=k
(k+x)³=3-x³
Δ=-3k²(k²+4), k=0

>> e=(2*x3+x-3)**3-3+x3
>>> solve(e)
[2**(2/3)*3**(1/3)/2, -2**(2/3)*3**(1/3)/4 - 2**(2/3)*3**(5/6)*I/4, -2**(2/3)*3**(1/3)/4 + 2**(2/3)*3**(5/6)*I/4, CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 0), CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 1), CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 2), CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 3), CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 4), CRootOf(4*x**6 + 6*x**4 - 12*x**3 + 3*x**2 - 9*x + 10, 5)]

---

x⁴-4x-1=0

令x²+1=k
x⁴+2x²+1=k²
k²-2x²-1-4x-1=0
k²=2(x+1)²

>>> e=x4-4*x-1
>>> solve(e)
[-sqrt(2)/2 - sqrt(-sqrt(2) - 1/2), -sqrt(2)/2 + sqrt(-sqrt(2) - 1/2), sqrt(2)/2 + sqrt(-1/2 + sqrt(2)), -sqrt(-1/2 + sqrt(2)) + sqrt(2)/2]