完整教程:Torch-Rechub学习笔记-task3
Torch-Rechub学习笔记-task3
以下以DatawhaleTorch—Rechub组队学习的Task笔记
[项目开源地址]: https://github.com/datawhalechina/torch-rechub
推荐系统排序模型
task2中主要是对推荐场景的排序部分进行探索学习
- 场景:排序(Ranking)
- 模型:DeepFM、DIN
- 数据集:Criteo、Amazon
特征交叉建模DeepFM
- 模型结构
DeepFM是对 Wide & Deep 架构的直接改进和优化。它将 Wide & Deep 中需要大量人工特征工程的 Wide 部分,直接替换为了一个无需任何人工干预的 FM 模型,从而实现了真正的端到端训练。更关键的是,DeepFM 中的 FM 组件和 Deep 组件共享同一份特征嵌入(Embedding)。这带来了两大好处:模型可以同时从原始特征中学习低阶和高阶的特征交互;其次,共享 Embedding 的方式使得模型训练更加高效。
DeepFM 的结构非常清晰,它由 FM 和 DNN 两个并行的组件构成,两者共享输入。
- FM 组件: 负责学习一阶特征和二阶特征交叉。其输出 yFM 的计算方式与标准 FM 完全相同:
- Deep 组件: 负责学习高阶的非线性特征交叉。它的输入正是 FM 组件中所使用的那一套 Embedding 向量。具体来说,所有输入特征首先被映射到它们的低维 Embedding 向量上,然后这些 Embedding 向量被拼接(concatenate)在一起,形成一个长的向量,作为 DNN 的输入。
最终,DeepFM 的总输出是 FM 部分和 Deep 部分输出的简单相加,再通过一个 Sigmoid 函数得到最终的点击率预测值。
DeepFM模型成功地结合了FM的低阶特征学习能力和深度神经网络的高阶特征学习能力。通过FM组件和深度组件共享相同的特征嵌入,模型可以同时从原始特征中学习低阶和高阶特征交互,无需像Wide & Deep那样依赖专家的特征工程。这种设计使得DeepFM成为一个端到端的自动特征学习模型,在效果和效率上都表现出色。
模型架构组成
DeepFM = Linear部分 + FM部分 + Deep部分
Linear部分(一阶特征交互)
学习特征的线性关系
等价于逻辑回归模型
FM部分(二阶特征交互)
通过向量内积建模特征间的二阶交互
解决稀疏数据下的特征交叉问题
Deep部分(高阶特征交互)
使用深度神经网络学习复杂的高阶特征交互
具备强大的非线性表达能力
核心优势
无需手工特征工程: 自动学习特征交叉,无需人工设计
同时建模低阶和高阶交互: FM处理二阶,Deep处理高阶
端到端训练: 三个部分共享embedding,联合优化
工业界验证: 在多个真实场景中取得显著效果提升
数学原理
DeepFM的预测公式为:
ŷ = sigmoid(y_linear + y_fm + y_deep)
其中:
y_linear: 一阶线性部分
y_fm: FM二阶交互部分
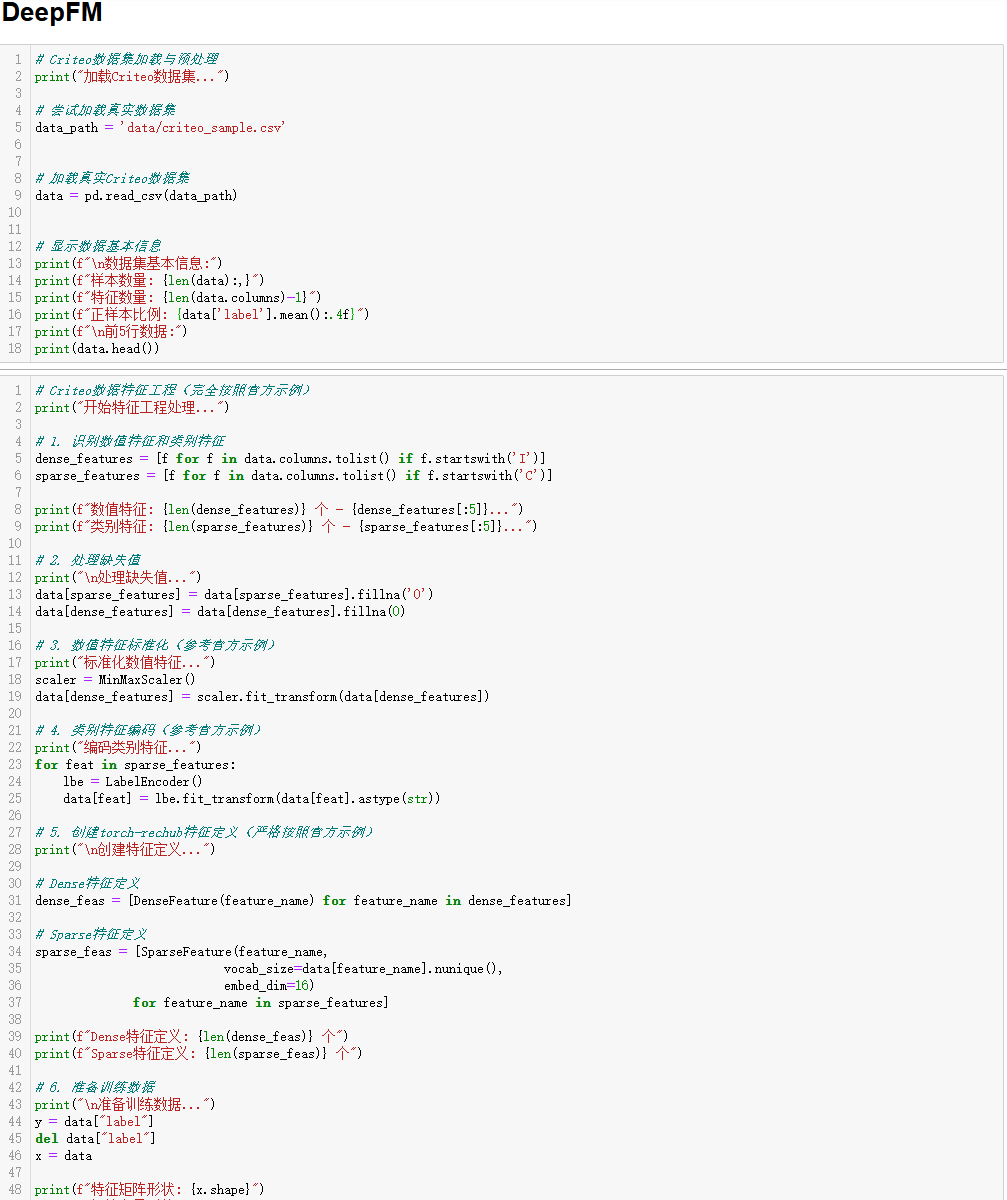
y_deep: 深度网络部分部分代码截图
序列建模DIN
- 模型结构
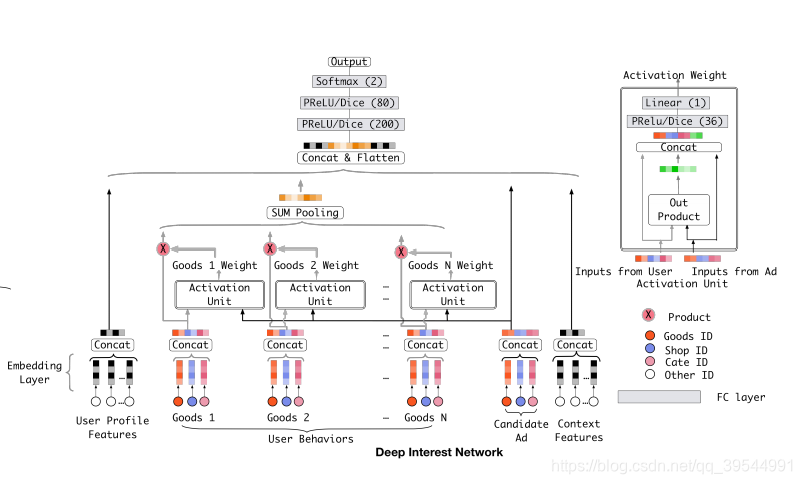
Deep Interest Network(DIIN)是2018年阿里巴巴提出来的模型,DIN的核心思想:局部激活 (Local Activation)。用户的某一次具体点击行为,通常只由其历史兴趣中的一部分所“激活”。当向一位数码爱好者推荐“机械键盘”时,真正起决定性作用的,很可能是他最近浏览“游戏鼠标”和“显卡”的行为,而不是他上个月购买的“跑鞋”。
基于此,DIN提出了一个观点:用户的兴趣表示不应该是固定的,而应是根据当前的候选广告(Target Ad)不同而动态变化的。
技术实现:注意力机制
为了实现“局部激活”这一思想,DIN在模型中引入了一个关键模块——局部激活单元(Local Activation Unit),其本质就是注意力机制。如模型结构图图右侧所示,DIN不再像基准模型那样对所有历史行为的Embedding进行简单的池化,而是进行了一次“加权求和”。
这个权重(即注意力分数)的计算,体现了DIN的核心思想。
一个值得注意的细节是,DIN计算出的注意力权重wj没有经过Softmax归一化。这意味着wj不一定等于1。这样设计的目的是为了保留用户兴趣的绝对强度。例如,如果一个用户的历史行为大部分都与某个广告高度相关,那么加权和之后的向量模长就会比较大,反之则较小。这种设计使得模型不仅能捕捉兴趣的“方向”,还能感知兴趣的“强度”。
DIN(Deep Interest Network)是阿里巴巴在2018年提出的创新性CTR预估模型,专门针对电商场景中用户兴趣的多样性和动态性问题
核心创新点
- 注意力机制(Attention Mechanism)
- 根据候选物品动态计算历史行为的重要性权重
- 解决传统模型中历史行为等权重处理的问题
- 用户兴趣多样性建模
- 认识到用户兴趣的多样性和动态性
- 不同候选物品激活不同的历史兴趣
- 自适应激活单元(Activation Unit)
- 设计专门的注意力网络结构
- 学习候选物品与历史行为的相关性
模型架构组成
DIN = 基础特征 + 注意力池化的历史特征 + 候选物品特
- 基础特征层
- 用户画像特征(年龄、性别、地域等)
- 上下文特征(时间、设备等)
- 历史行为序列层
- 用户历史点击/购买物品序列
- 历史物品的类别序列
- 注意力机制层
- 计算历史行为与候选物品的相关性
- 生成动态的注意力权重
- 候选物品特征层
- 当前候选物品的特征
- 用于与历史行为计算注意力
注意力机制原理
DIN的核心是Activation Unit,其计算过程为:
attention_weight = ActivationUnit(candidate_item, history_item) weighted_history = Σ(attention_weight * history_embedding)应用场景优势
- 电商推荐: 用户购买意图随商品变化
- 内容推荐: 用户兴趣点多样且动态
- 广告推荐: 需要精准捕获用户当前兴趣
部分代码截图
学习思考以及心得
本次Task3的两个模型都是非常经典的排序模型。DeepFM是非常通用的CTR预估任务模型,在广告点击率预估、商品推荐点击预测、商品推荐点击预测都有非常好的效果。而DIN在电商推荐场景、用户行为序列丰富也有很好的效果。在工程的实践中,对数据的缺失值和异常值处理、序列特征处理等需要特别关注。而在模型的优化上,需要在超参(Embedding维度、网络结构、学习率)和正则化(Dropout、早停等)上关注。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/945233.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!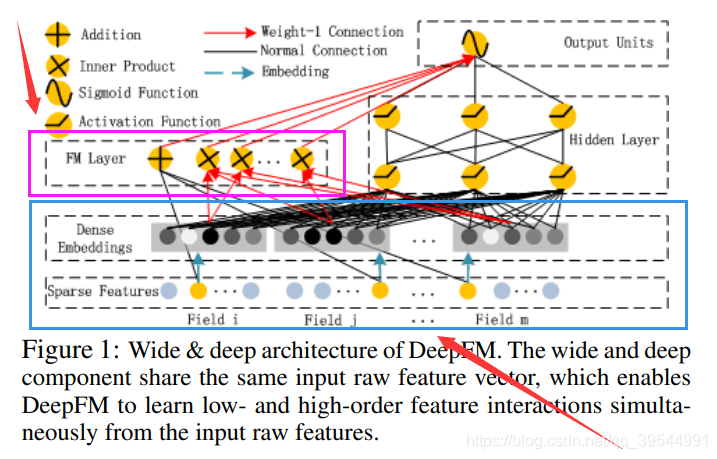



)

)


 - 教程)

)








)


)