一、Swagger
Swagger是一个用于生成、描述、文档化可视化API的工具(框架)。直接使用Swagger会比较繁琐,所以我们用到了Knife4j框架,它对Swagger进行了封装,简化了相应的操作。
1、Knife4j的使用方式:
(1)导入Knife4j的maven坐标

(2)在配置类中加入Knife4j相关配置

指定生成接口要扫描的包:com.sky.controller
这里面的类、方法、属性都扫描到,通过反射来解析这些,最终生成接口文档。
(3)设置静态资源映射,否则接口文档页面无法访问到
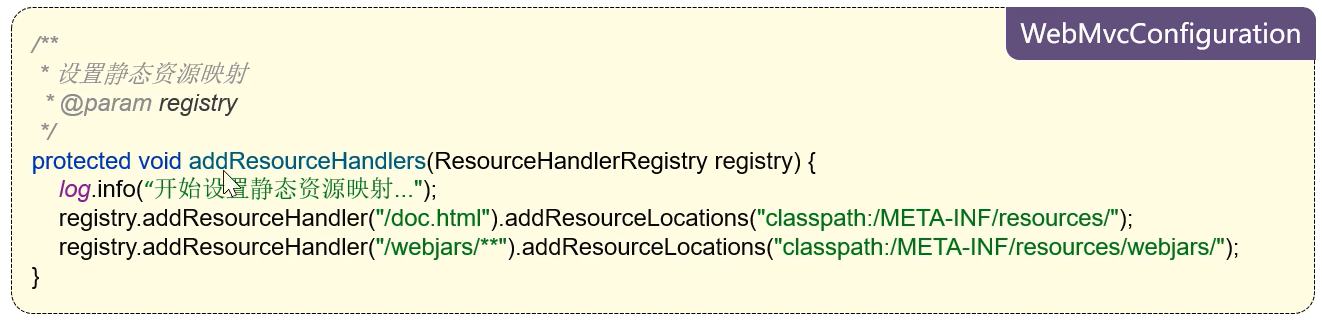
如果我们没有设置静态资源映射,当访问localhost:8080/doc.html时,SpringMVC框架会不认为我们访问的是静态资源,它会以为我们访问的是某个controller。
YAPI是设计阶段使用的工具,管理和维护接口。
Swagger是在开发阶段使用的框架,帮助后端开发人员做后端的接口测试。
2、Swagger常用注解

这些注解标在该标的位置上面后,文档里就会生成对应的描述信息。描述类是干嘛的、方法是干嘛的、属性代表什么意思。
二、@RequestParam和@RequestBody的使用场景
@RequestParam通常用于GET请求,接收的参数形式是key-value形式,要求请求头中的content-type字段值是application/x-www-form-urlencoded;
@RequestBody通常用于接收前端发来的json串,请求头中的content-type字段值可以是application/json或者application/xml。
Content-type字段用于指定请求体的媒体类型,帮助服务器理解请求体中数据格式。
三、@PostMapping和@RequestMapping的区别
@PostMapping特定于Post请求,表明该方法处理的是Post请求,增加了代码的可读性和意图明确性。后面可以添加路径; = @RequestMapping(method = RequestMethod.POST)
@RequestMapping可以用来指定多种类型的HTTP请求(GET、POST、PUT、DELETE等),可以用过method属性来指定特定类型,后面也可以添加路径、属性等。
四、对象属性拷贝
使用EmployeeDTO是为了方便封装前端传来的数据,但最终传给持久层还是建议用实体类,所以要把DTO中的属性拷贝给实体类。(前提是对应的属性名要一致,并且剩下的属性逐个set)
BeanUtils.copyProperties(employeeDTO, employee);
五、@Insert注解
当我们只是进行简单的数据库操作时,就没有必要在xml文件中写SQL语句了,直接在Mapper层的方法上标注@Insert注解,里面写SQL语句就好。

注意这里的对应关系,数据库中的是id_number,但实体类employee中的字段是idNumber驼峰命名。如果想要在这里能对应上,需要在application.yml配置文件中开启驼峰命名。
map-underscore-to-camel-case: true












)






