吴恩达深度学习课程一：神经网络和深度学习 第二周：神经网络基础（三）

此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第一课第二周，是2.4到2.6部分的笔记内容。
可能会发现跳过了几节，实际上是因为课程中的顺序为讲解结构后再分别讲解基础的顺序，笔记为了便于理解，便改为先讲解基础后可以顺畅的理解结构的顺序。跳过的节数会在之后再讲到。

---

本周的课程以逻辑回归为例详细介绍了神经网络的运行，传播等过程，其中涉及大量机器学习的基础知识和部分数学原理，如没有一定的相关基础，理解会较为困难。
因为，笔记并不直接复述视频原理，而是从基础开始，尽可能地创造一个较为丝滑的理解过程。

首先，经过之前的第二部分内容学习，我们了解了机器学习中的分类是什么以及逻辑回归算法，而本篇延续逻辑，进行传播部分的讲解。这一部分则涉及较多的数学基础，同样会在笔记中进行补充，本篇更偏向于补充数学基础。

依旧以一个问题来引入，现在我们知道了逻辑回归如何得到分类结果，但想要预测结果更准确，拟合效果更好，我们便要寻找使结果最优的权重 \(w\) 和偏置 \(b\) ，那如何得到这两个数呢？
我们以此开始本篇笔记的内容。

1.导数

要寻找使结果最优的权重 \(w\) 和偏置 \(b\)，便要以一种合适的规则来对二者不断地更新，得到最优的结果，什么样的更新方法最好最合适，这便涉及到效率问题，而当我们想提高效率时，总是离不开数学的。 导数便是这一部分的基础。

1.1 什么是导数？

老样子先摆一个导数的概念：

导数是一个基本的数学概念，主要用于分析函数的变化率。简单来说，导数表示一个函数在某一点的瞬时变化率，或者说是该点切线的斜率。

斜率的概念我们不陌生，两点确定一条直线，用两点纵横坐标的差作除法，就得到这了这条直线的斜率。
为了便于理解的同时不涉及太多的数学内容，我们先不摆导数的公式，用课程中的例子来进行说明：

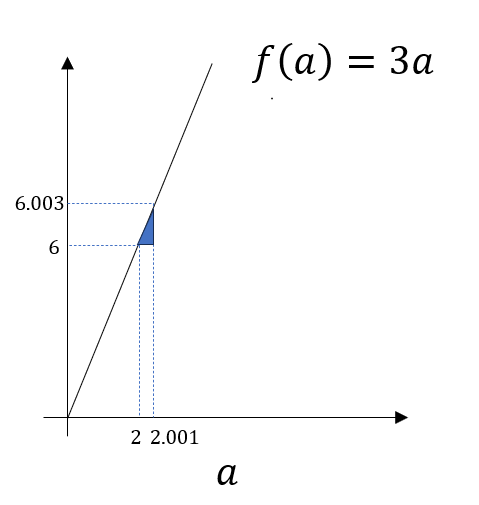
如图，这是一个函数图像，我们标记了当 \(a_1=2和a_2=2.001\) 的两点，而这两点对应的函数值\(f(a_1)=6和f(a_2)=6.003\) , 连接两点和其对应的移动距离便构成图中的小三角形，我们不难得到这样的结论：
当我们把 \(a\) 从2向上移动了0.001时，其对应的函数值增加了0.003，即这条直线的斜率为3。
而刚刚在概念里提到，导数是一个点切线的斜率，问题来了，当我们只知道切点的时候，如何才能的得到这个点切线的斜率？
这便涉及微积分中极限的概念，我们现在再来看导数的公式：

\[f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} \]

简单解释一下：

1. \(f'(a)\) 就代表 \(f(a)\) 的一阶导数。
2. \(lim_{h \to 0}\) 代表 \(h\) 是一个无限趋近于0，非常非常小的增量，比例里的0.001还要小的多，无法度量。
   只有在这样的情况下，我们连接 \(f(a+h) 和 f(a)\) 得到的才是 \(a\) 点的切线，如图所示（例）：
   

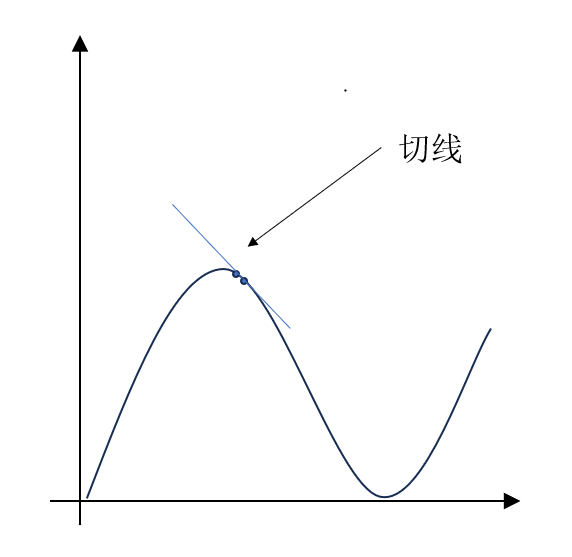
知道了如何得到导数后，现在我们回到刚刚的两个 \(a\) 点上，结合刚刚的概念，我们便得到如下结论：
假设0.001可以当作 \(h\) 时，函数 \(f(a)=3a\) 在\(a=2\) 这一点的（一阶）导数值为3。
可以发现我们强调了导数值是针对一个具体的点所说的，而斜率往往针对一条线，这便是二者在概念上的其中一点不同。
继续看\(f(a)=3a\) 这个函数，我们会发现，其实这个函数在任何一点上的导数值都是3，因为它的任何一点的切线都是函数图像本身，再说斜率，在这个函数里，无论取相隔多远的两个点，其产生的函数值的变化都是都是3倍。
对这个简单的函数，我们无需多想，便可以得出 $$f'(a)=3$$
这代表 \(f(a)\) 在任何一点的导数值都等于3，不同于刚刚只针对一个点的说法，\(f'(a)\) 描述了原始函数在每一点的瞬时变化率，我们便称之为导函数。

1.2 如何得到导函数？

刚刚通过一个导函数恒定的例子来解释导数，但实际上想得到导函数，找到函数变化的规律不会这么简单，我们来看一个更复杂的情况：

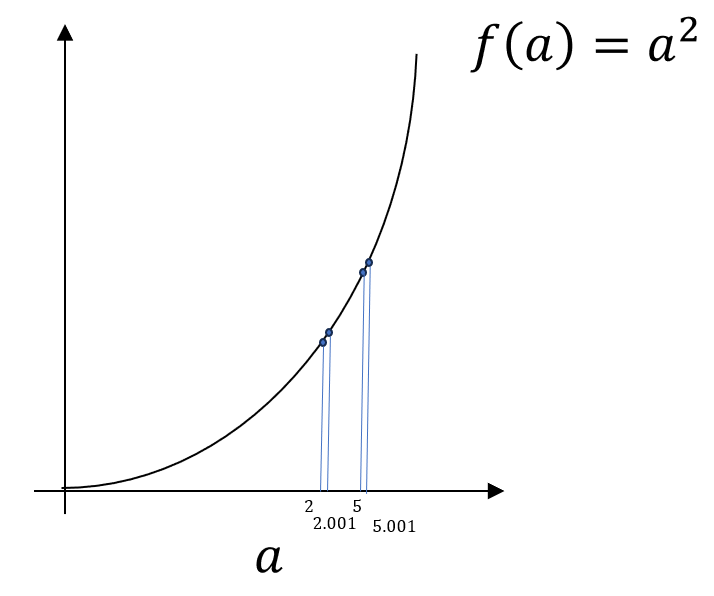
不再重复赘述过程。
经过计算，我们可以发现，函数 \(f(a)=a^2\) 在\(a=2\) 这一点的（一阶）导数值为4，在\(a=5\) 这一点的（一阶）导数值为10。
这说明导函数和函数一样，也需要变量。
先摆结论：

\[f(a)=a^2时，f'(a)=2a \]

这是查表得到的，不多描述原理，简单来说，各种基本函数有其规律可以总结出其导函数，而复杂函数也就是基本函数的组合，同样可以通过运算得到其导函数。
在这里，我们只需要知道，我们用导函数得到函数在各个点的瞬时变化率，而我们只要查表得到导函数即可。

1.3 如何得到多变量函数的导函数？

我们已经知道如何得到单变量的导函数了，现在再扩展一下，当变量从单个变为两个甚至多个的时候呢？
实际上，多变量的函数才是更符合神经网络的，因为我们大多情况下都不会只输入一种特征，而往往是多种特征来作为输入。
现在我们来看这样一个函数：

\[f(x,y)=3x+2y^2 \]

这个函数有两个变量，而且这两个变量互不相关，如何求这样同时有两个量变化的函数的导函数？
现在摆一个偏导数的概念：

偏导数是多变量函数最常见的求导方式，适用于多变量函数中，求某一特定变量对函数的影响。它计算的是在其他变量固定不变时，函数相对于某一变量的变化率。

计算偏导数的步骤与普通导数类似，只是要记住在求某个变量的偏导数时，其他变量视为常数。
我们来进行一下 \(f(x,y)=3x+2y^2\) 分别对变量 \(x和y\) 的偏导数。
看一下偏导数的表示方式及其对应的结果：

\[f(x,y)对x的偏导数表示：\frac{\partial f(x,y)}{\partial x} = 3 \]

\[f(x,y)对y的偏导数表示：\frac{\partial f(x,y)}{\partial y} = 4y \]

要说明的一点是，单个变量函数的导函数也有类型的书写格式，但可能会造成混淆。在笔记中只使用\(f'(a)\) 这样较简洁的格式，大家可以自行了解。

现在，我们得到了d \(f(x,y)对x和y的偏导数\) ,这两个偏导数便代表了两个变量分别对函数的影响，其变化率。

这一节其实全部是在补充数学方面的基础，在了解了导数方面的基础后，这些知识到底怎么帮助我们训练权重\(w\)和偏置\(b\) 呢？我们展开下一部分。

2.梯度下降法

2.1 什么是梯度？

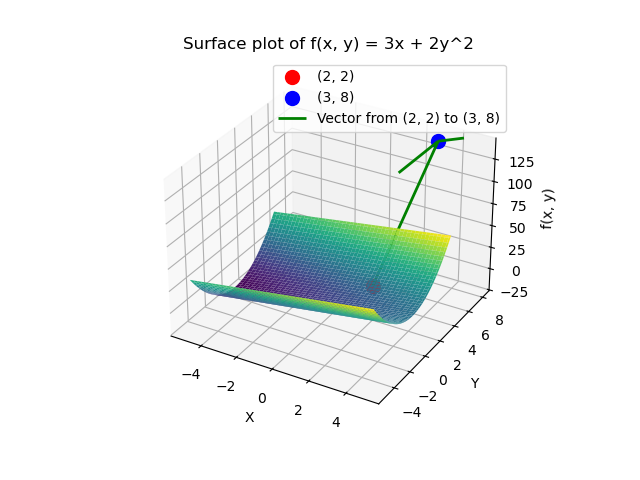
我们知道了怎么求多变量的导函数，现在再看一下\(f(x,y)=3x+2y^2\)的图像：

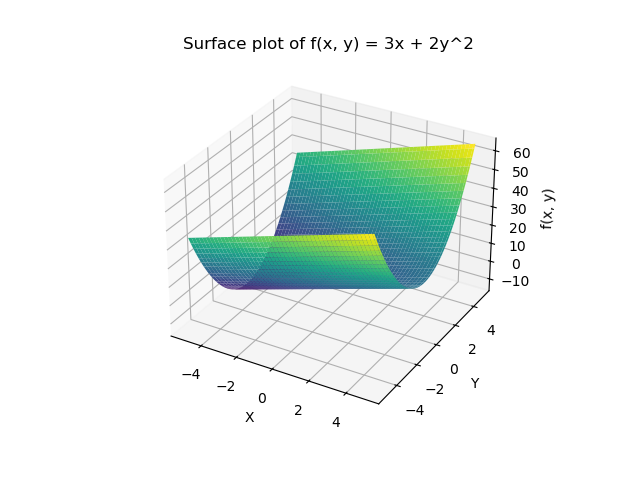
我们已经通过偏导数知道了在函数任意一点上，该点在 \(x\) 方向和 \(y\) 的变化率，简单举例解释，在\((2,2)\) 这个点上，函数在 \(x\) 方向和 \(y\) 的变化率为\(3和8\) 。
于是我们便知道了在这一点上，函数在 \(y\) 方向变化的比在 \(x\) 方向上的变化更快。
通俗来说，把图像看作山坡，在这一点的位置上， \(y\) 方向比 \(x\) 方向更“陡”。
可问题又来了，不同于单变量函数只能一条线上移动，当变量增加为两个，图像也由线扩展为面，同样以山坡为例，我们不仅可以单独改变 \(x或者y\) ，也就是“直着走”，我们也可以同时改变\(x和y\)，来“斜着走”。
在这样的情境下，函数图像就是真正的山坡，而我们站在某一点的位置上，只要不“穿模”（走到图像外），便可以向山坡的任何方向移动。
由此，我们引入梯度的概念：

梯度是由函数的偏导数组成的向量，每个分量表示该函数在对应变量方向的变化速率。梯度的方向是函数值变化最快的方向，而梯度的大小则表示在该方向上的变化率的大小。

依旧以\(f(x,y)=3x+2y^2\) 来说明这个概念,已知梯度向量是由函数的偏导数组成的向量,那么本题中的梯度向量就是:

\[\nabla f(x, y) = \left( \frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial y} \right) = \left( 3, 4y \right) \]

我们现在站在\((2,2)\) 上,即:

\[\nabla f(2, 2) = \left( 3, 8 \right) \]

我们再通过叙述理解一下这两个式子:

首先,我们将函数对两个变量的偏导数组合成立一个二维向量,这个向量的每个元素代表都代表一个变量在该方向的变化率。
而当我们代入具体位置时，便得到对应的梯度向量,这两个变化率组合成一个二维向量，这个向量指向的便是变化最快的方向。
我个人的理解来说，针对两个变量的函数，它在x,y的方向的偏导就像直角三角形的两条直角边，得到的斜边最长，其指向的方向就是变化最快的方向，而换一个方向，这个角就不一定是直角。
总而言之,梯度指向的是局部变化速率最大的位置。
如下图所示，\((3,8)\)的方向即是在\((2,2)\)时，移动时让函数值变化最大的方向。也就是“最陡的方向”。

这里我们通过例子说明的梯度是什么，实际上如果还想更深入的理解，可以再了解一下方向导数，如何理解梯度(方向导数的最大值） 这为up主的视频可以很好的讲解。
但是涉及到向量计算，我们只在这里理解梯度的含义，便于服务神经网络即可。

2.2 什么是梯度下降法

回到神经网络里来，我们之前在第一周的课程里提过，监督学习就是学生可以在考试-对答案-考试的重复中不断提高自己的成绩。
而要不断提升模型效果，我们就要让每一次对答案时，我们的作答和答案的差别越来越小，只有这样，我们才能达到训练的效果。
也就是说，训练权重\(w\)和偏置\(b\)，可以看做一个输出和标签的差别最小化问题。
我们把计算所有输出和标签的总差别的函数叫做成本函数，我们在了解完梯度下降法后再聊它们。
而怎么最快的找到最佳的参数，让成本函数的结果最小，其实从梯度下降法的名字就可以看出来了。

我们通过梯度得知了函数值变化最快的方向，而又根据导数本身的定义我们又知道了梯度的方向其实是上升的方向。
那么，当我们想要让函数值最小时，只要顺着梯度的反方向走，即梯度下降的方向走，不就能最快的达到最小值，从山坡下到平地了吗？
现在给出梯度下降法的概念：

梯度下降法是一种优化算法，常用于在多维空间中找到一个函数的最小值。简而言之，它就是通过沿着梯度的反方向（即最快下降的方向）一步步更新参数，直到找到函数的最低点。

至此，我们知道了训练权重\(w\)和偏置\(b\) 的方法，实际上，梯度下降法还有一些可能导致的问题，它在实际的传播过程中又如何应用，我们便在下一篇进行逻辑回归传播过程的具体讲解。