1.1 采样问题 Sampling and Bandits

n臂bandits（n-armed bandits）

n臂bandits（multi-armed bandit）是最简单的试错式学习形式。学习与动作选择都发生在同一个状态中，在该状态下有 \(n\) 个可用动作，每个动作对应不同的奖励分布。目标是通过试错的方式找出哪个动作在平均意义上能获得最多的奖励。

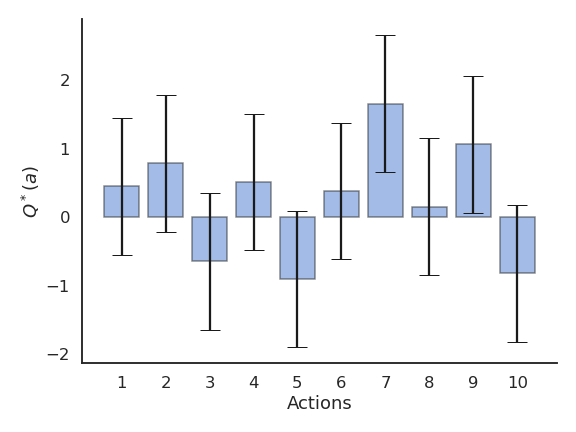
我们可以在 \(N\) 个不同的动作 \((a_1, ..., a_N)\) 中进行选择。每次在时间 \(t\) 采取动作 \(a\) 时，会获得一个奖励 \(r_t\)，该奖励是从与动作相关的概率分布 \(r(a)\) 中抽样得到的。

该分布的数学期望即为该动作的期望奖励，也称为该动作的真实价值 \(Q^*(a)\)：

\[ Q^*(a) = \mathbb{E} [r(a)] \]

奖励分布还具有方差，但在强化学习（RL）中我们通常忽略它，因为我们主要关心的是最优动作 \(a^*\)（不过在分布式强化学习中我们会重新考虑方差）：

\[a^* = \text{argmax}_a \, Q^*(a) \]

如果我们无数次地选择最优动作，我们就能平均意义上最大化奖励。
问题在于：如何通过试错找出最优动作？
也就是说，在不知道奖励分布 \(r(a)\) 的情况下，我们只能通过采样获得其样本。

\[r_t \sim r(a) \]

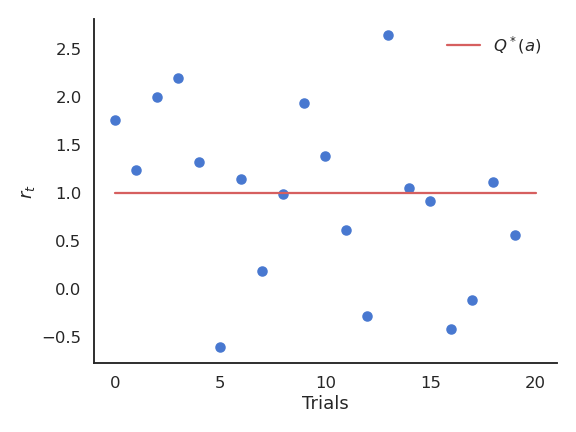
接收到的奖励 \(r_t\) 随时间在真实值附近波动。
我们需要基于采样结果建立每个动作的价值估计 \(Q_t(a)\)。这些估计在开始时会非常不准确，但会随着时间逐渐变好。

---

随机采样（Random sampling）

期望（Expectation）

随机变量的一个重要指标是其数学期望或期望值。
对于离散分布，它是每个可能结果乘以对应概率后的加权平均：

\[ \mathbb{E}[X] = \sum_{i=1}^n P(X = x_i) \, x_i \]

对于连续分布，则需要对其概率密度函数（pdf）进行积分：

\[ \mathbb{E}[X] = \int_{x \in \mathcal{D}_X} f(x) \, x \, dx \]

同样可以计算随机变量函数的期望：

\[ \mathbb{E}[g(X)] = \int_{x \in \mathcal{D}_X} f(x) \, g(x) \, dx \]

---

随机采样（Monte Carlo Sampling）

在机器学习和强化学习中，我们通常面对概率分布未知的随机变量，但仍然关心其期望或方差。

随机采样或蒙特卡洛采样（MC）指从分布 \(X\)（离散或连续）中取 \(N\) 个样本 \(x_i\)，并计算样本平均值：

\[ \mathbb{E}[X] = \mathbb{E}_{x \sim X} [x] \approx \frac{1}{N} \, \sum_{i=1}^N x_i \]

当 \(f(x)\) 较大（即 \(x\) 概率较高）时，采样到的次数也较多，因此样本平均值会接近真实的期望值。

大数定律（Law of Large Numbers）
当随机变量的数量增加时，其样本均值会趋近于理论均值。

MC 估计只有在以下条件下才正确：

1. 样本必须是独立同分布（i.i.d.）的；
2. 样本数量足够大。

同理，可以估计随机变量的任意函数：

\[ \mathbb{E}[f(X)] \approx \frac{1}{N} \sum_{i=1}^N f(x_i) \]

---

中心极限定理（Central Limit Theorem）

假设我们有一个未知分布 \(X\)，其期望为 \(\mu = \mathbb{E}[X]\)，方差为 \(\sigma^2\)。
随机取 \(N\) 个样本并计算样本均值：

\[ S_N = \frac{1}{N} \, \sum_{i=1}^N x_i \]

中心极限定理
样本均值的分布服从均值为 \(\mu\)、方差为 \(\frac{\sigma^2}{N}\) 的正态分布：

\[S_N \sim \mathcal{N}(\mu, \frac{\sigma}{\sqrt{N}}) \]

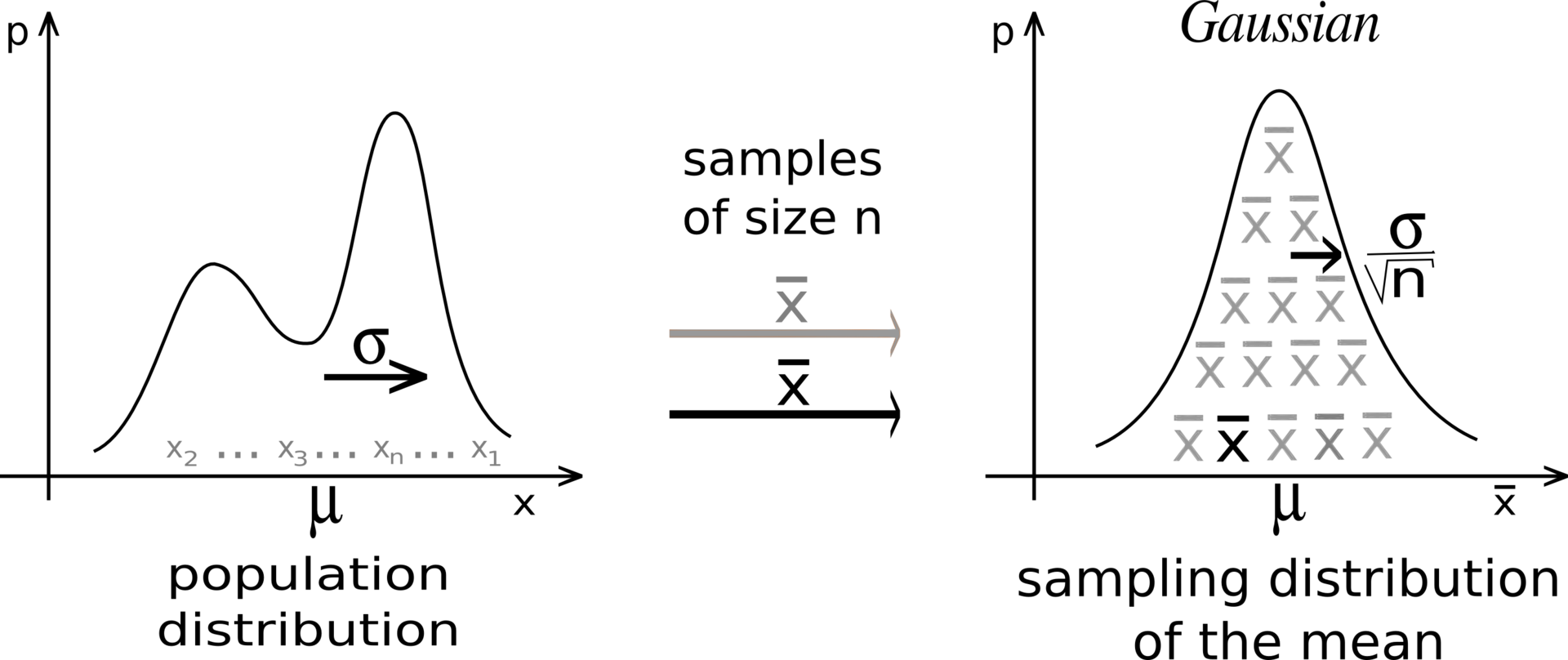
这说明样本均值是分布期望的无偏估计量：

\[\mathbb{E}(S_N) = \mathbb{E}(X) \]

估计量（estimator）是用于估计分布参数的随机变量，但估计量可能存在偏差。

例如，假设温度 \(T\) 是一个服从正态分布（\(\mu=20, \sigma=10\)）的随机变量，温度计 \(M\) 的测量关系为：

\[ M = 0.95 \, T + 0.65 \]

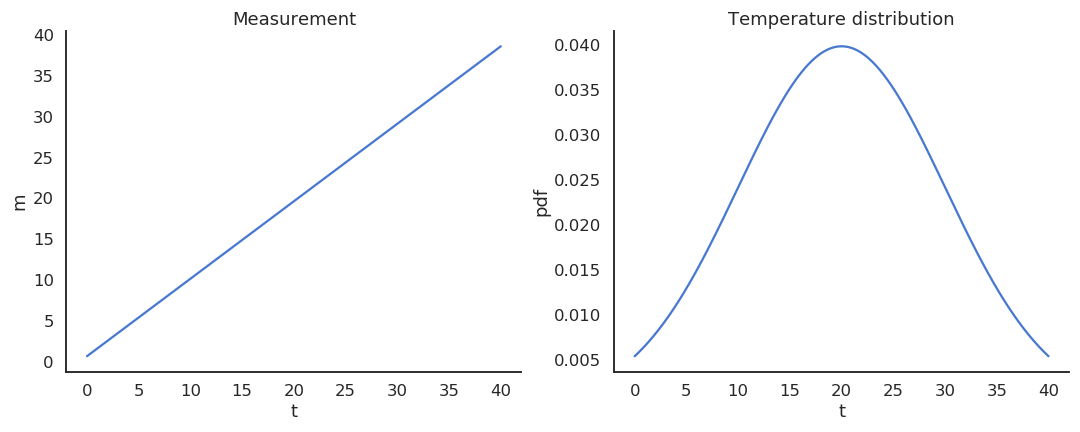
此时：

\[ \mathbb{E}[M] = 0.95 \, \mathbb{E}[T] + 0.65 = 19.65 \neq \mathbb{E}[T] \]

因此，温度计是温度的有偏估计量。

估计量的偏差（bias）定义为：

\[ \mathcal{B}(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta \]

而其方差（variance）为：

\[ \text{Var}(\hat{\theta}) = \mathbb{E}[(\hat{\theta} - \mathbb{E}[\hat{\theta}] )^2] \]

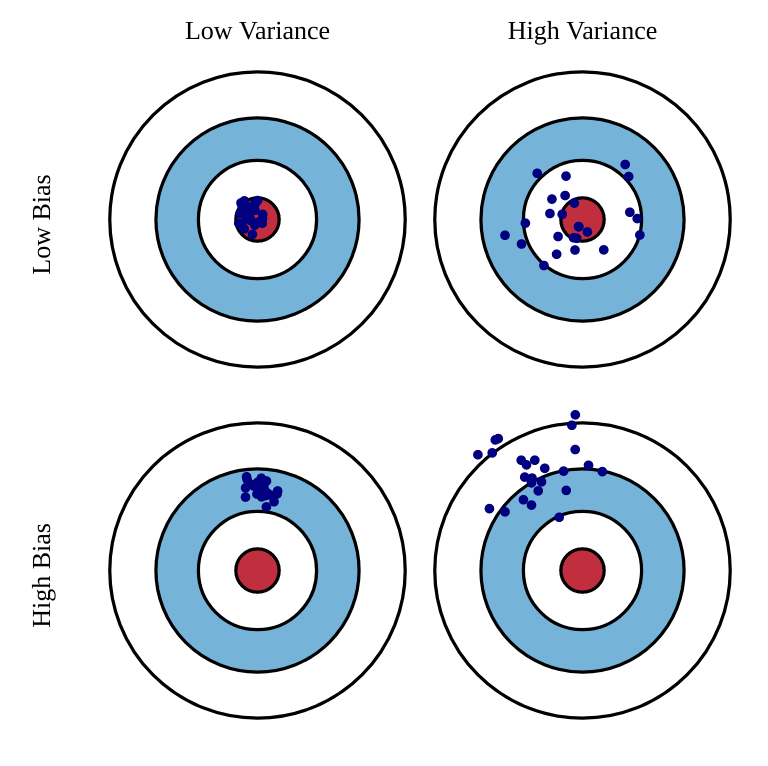
理想情况下，我们希望估计量既低偏差又低方差。但实际中，这两者存在权衡关系，即偏差-方差权衡（bias-variance trade-off）：

---

基于采样的估计（Sampling-based evaluation）

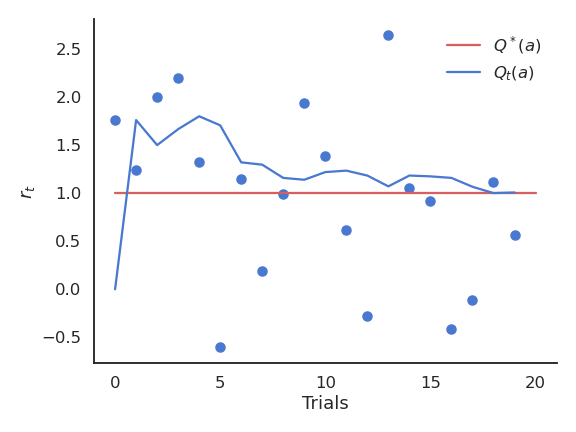
奖励分布的期望可以用采样均值来近似：

\[ \mathbb{E} [r(a)] \approx \frac{1}{N} \sum_{t=1}^N r_t |_{a_t = a} \]

当动作 \(a\) 被选择了 \(t\) 次后：

\[ Q_t (a) = \frac{r_1 + r_2 + ... + r_t }{t} \]

随着时间推移：

\[ \lim_{t \to \infty} Q_t (a) = Q^* (a) \]

可以用在线（online）方式更新均值估计：

\[ Q_{t+1}(a) = Q_t(a) + \frac{1}{t+1}(r_{t+1} - Q_t(a)) \]

如果奖励分布是非平稳（non-stationary）的，则 \(\frac{1}{t+1}\) 会太小，更新变慢。
此时用固定步长参数（学习率）\(\alpha\) 替换之：

\[ Q_{t+1}(a) = Q_t(a) + \alpha (r_{t+1} - Q_t(a)) \]

该形式称为指数滑动平均（EMA）。

更新规则总结为：

\[ \text{新估计} = \text{当前估计} + \alpha (\text{目标} - \text{当前估计}) \]

---

动作选择（Action selection）

我们已得到当前的 \(Q_t(a)\) 估计，接下来应选哪个动作？

贪婪策略（Greedy）

贪婪动作为：

\[ a^*_t = \text{argmax}_{a} Q_t(a) \]

贪婪策略总是选择当前估计值最高的动作，但这可能导致陷入局部最优。

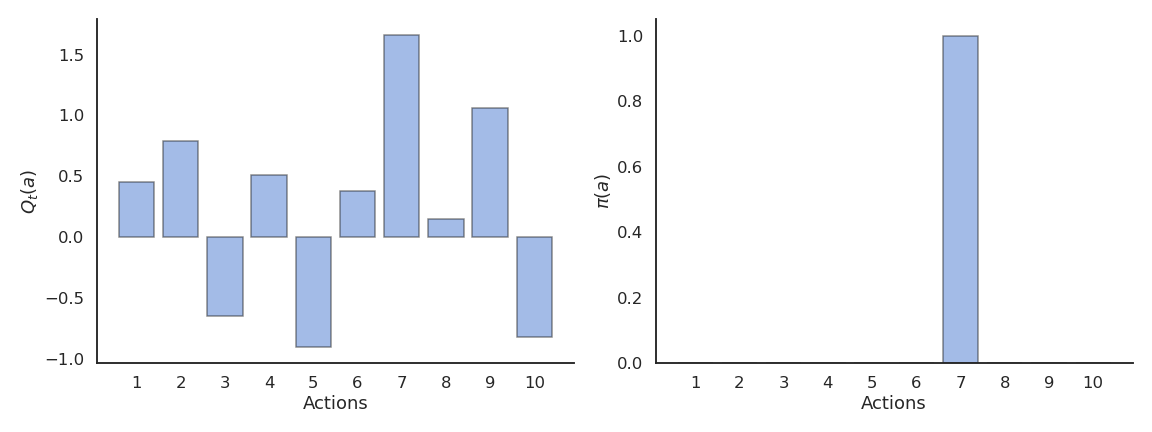
探索-利用（exploration-exploitation）困境：

• 利用：使用当前估计选择最佳动作（但可能错误）；
• 探索：尝试其他动作以改进估计。

通常做法是：

• 初期更多探索；
• 后期更多利用。

---

\(\epsilon\)-贪婪策略（\(\epsilon\)-greedy）

以概率 \(1-\epsilon\) 选择贪婪动作，以概率 \(\epsilon\) 随机选择其他动作：

\[ \pi(a) = \begin{cases} 1 - \epsilon, & a = a_t^* \\\frac{\epsilon}{|\mathcal{A}| - 1}, & \text{否则}\end{cases} \]

---

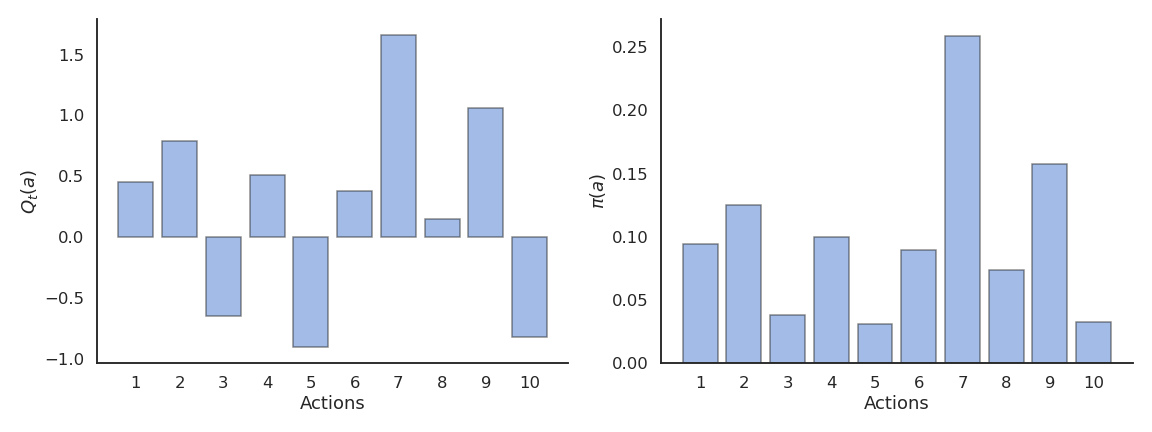
Softmax 动作选择

通过软最大分布（Gibbs/Boltzmann 分布）选择动作：

\[ \pi(a) = \frac{\exp(Q_t(a)/\tau)}{\sum_{a'} \exp(Q_t(a')/\tau)} \]

温度参数 \(\tau\) 控制探索程度：

• 高温 → 动作几乎等概率；
• 低温 → 只选贪婪动作。

---

乐观初值（Optimistic initial values）

若初始 \(Q_0\) 较大，则所有动作都会被尝试，从而自然实现探索。
但会导致初期的高估。

---

强化比较（Reinforcement comparison）

仅维护每个动作的偏好值 \(p_t(a)\)：

\[ p_{t+1}(a_t) = p_t(a_t) + \beta (r_t - \tilde{r}_t) \]

其中 \(\tilde{r}_t\) 是平均奖励的滑动估计。
动作的选择概率：

\[ \pi_t (a) = \frac{\exp p_t(a)}{\sum_{a'} \exp p_t(a')} \]

此思想是演员-评论家（actor-critic）架构的核心。

---

梯度bandit算法（Gradient bandit）

与强化比较类似，但还会减少非执行动作的偏好：

\[ p_{t+1}(a_t) = p_t(a_t) + \beta (r_t - \tilde{r}_t)(1 - \pi_t(a_t)) \]

\[ p_{t+1}(a) = p_t(a) - \beta (r_t - \tilde{r}_t)\pi_t(a), \quad a \neq a_t \]

---

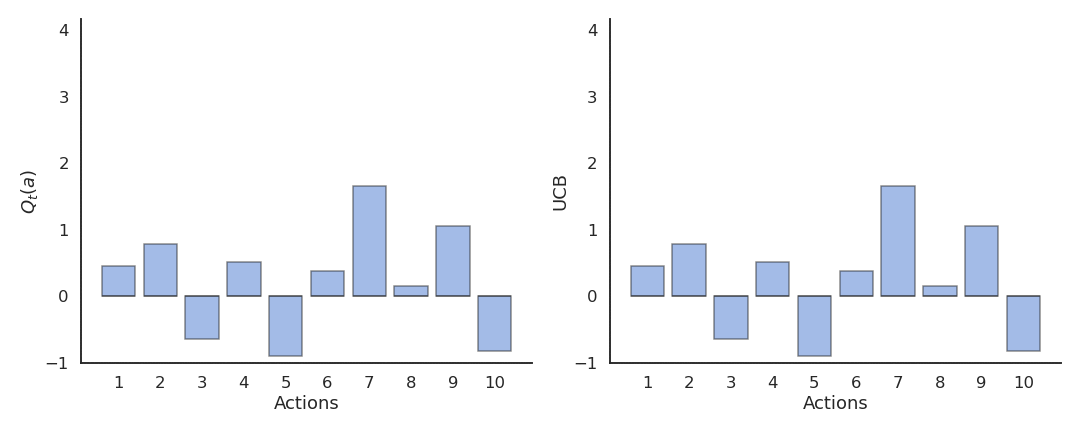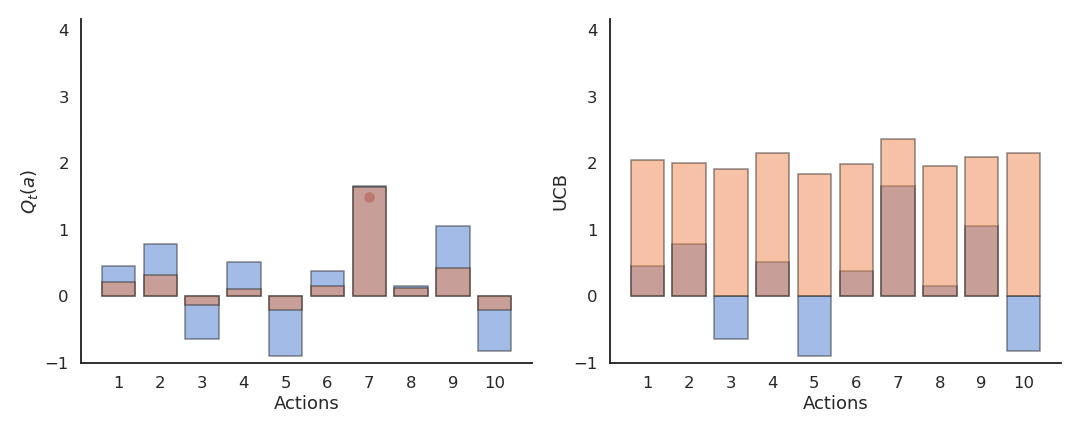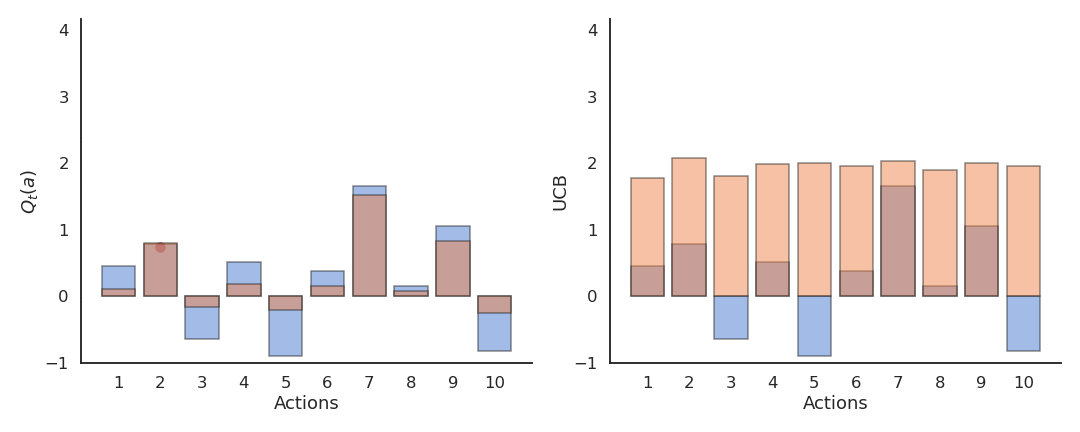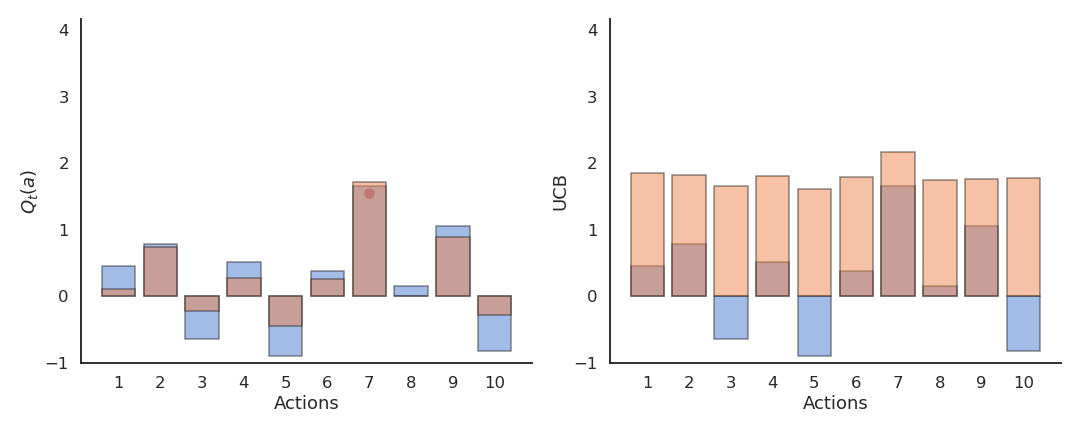
上置信界（UCB）动作选择

基于对动作价值的不确定性（方差）自动平衡探索与利用：

\[ a^*_t = \text{argmax}_{a} \left[ Q_t(a) + c \sqrt{\frac{\ln t}{N_t(a)}} \right] \]

其中：

• \(Q_t(a)\) 是当前估计；
• \(N_t(a)\) 是动作 \(a\) 被选择的次数；
• \(c\) 控制探索程度。

当某动作被探索次数少时，第二项较大，会鼓励探索；
当动作被充分探索时，第二项趋近于0，策略趋向贪婪。