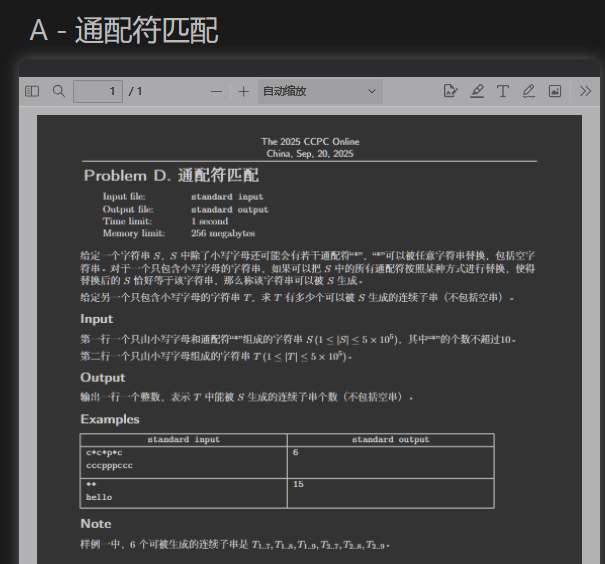
因为*最多只会有10个,所以被它截断成的串也很少。
每个串跑一边kmp得到匹配序列,然后DP即可
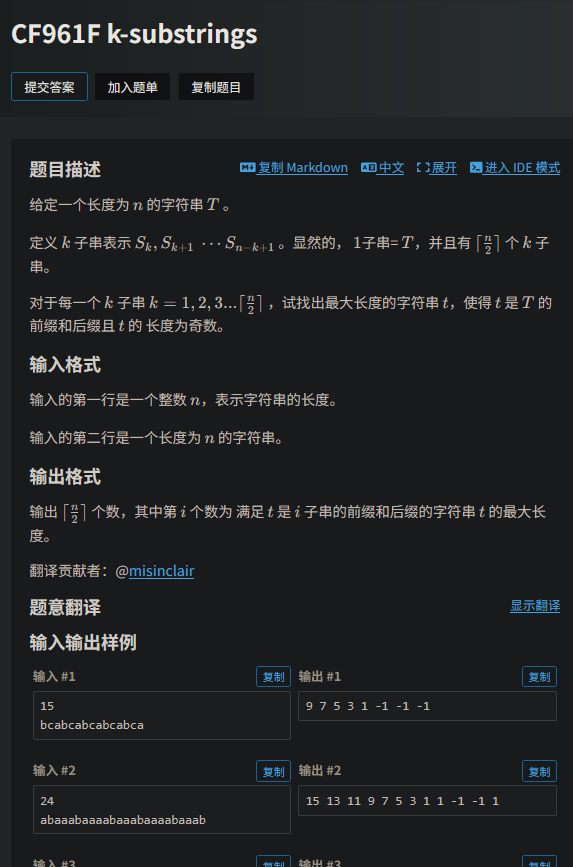
发现每次扩展一个字符的时候broder的增加是有限的。
我们每次扩展它最大+2,我们默认他+2,然后check,不符合再缩减直到符合,用哈希验证即可,但是需要双哈希。
势能分析以下显然复杂度没问题
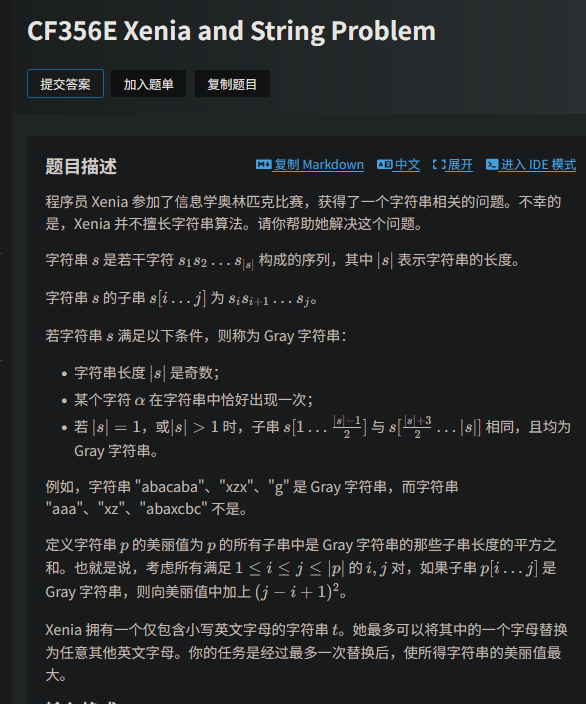
串的长度只有logn种,并且串一定回文,总共也就最多n log n种串,直接哈希计算

所以枚举修改位置和修改后字符,有26*n种方案。
然后剩下的就是分类讨论了。

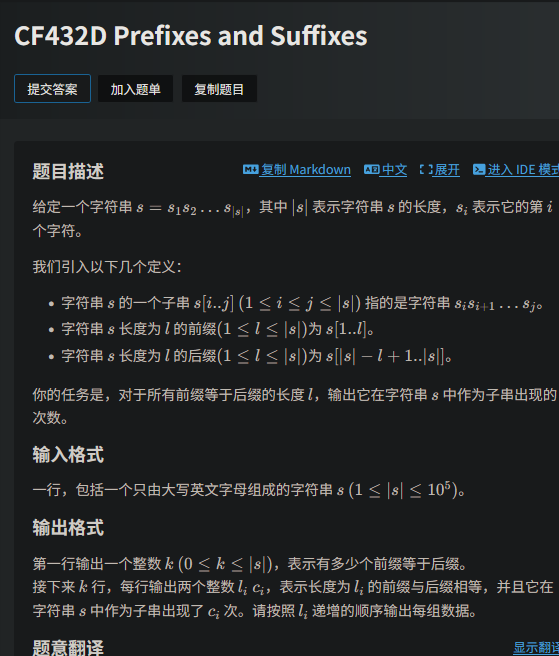
发现从n一直跳kmp的next,一定能出现所有broder。
然后直接DP
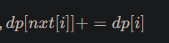
一个很有趣的结论就是如果串[l,r]有k循环节
那么[l,r-k+1] === [l+k-1,r]
所以直接线段树维护哈希check即可,这个也要双哈希
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int MOD1 = 1000000007;
const int MOD2 = 1000000009;
const int BASE = 91138233;struct Node {int len;ll h1, h2;int lazy;Node() : len(0), h1(0), h2(0), lazy(-1) {}
};struct QueryRes {ll h1, h2;int len;
};int n, m, k;
string s;
vector<ll> p1, p2, ones1, ones2;
vector<Node> seg;inline ll modmul(ll a, ll b, int mod) {return (a * b) % mod;
}void pull(int idx) {Node &cur = seg[idx];Node &L = seg[idx<<1];Node &R = seg[idx<<1|1];cur.len = L.len + R.len;cur.h1 = (L.h1 + modmul(R.h1, p1[L.len], MOD1)) % MOD1;cur.h2 = (L.h2 + modmul(R.h2, p2[L.len], MOD2)) % MOD2;
}void apply_set(int idx, int v) {seg[idx].lazy = v;seg[idx].h1 = modmul(v, ones1[seg[idx].len], MOD1);seg[idx].h2 = modmul(v, ones2[seg[idx].len], MOD2);
}void push(int idx) {if (seg[idx].lazy != -1 && seg[idx].len > 1) {apply_set(idx<<1, seg[idx].lazy);apply_set(idx<<1|1, seg[idx].lazy);seg[idx].lazy = -1;}
}void build(int idx, int l, int r) {seg[idx].lazy = -1;if (l == r) {seg[idx].len = 1;int v = s[l-1] - '0';seg[idx].h1 = v % MOD1;seg[idx].h2 = v % MOD2;return;}int mid = (l + r) >> 1;build(idx<<1, l, mid);build(idx<<1|1, mid+1, r);pull(idx);
}QueryRes qry(int idx, int l, int r, int ql, int qr) {if (ql <= l && r <= qr) {return {seg[idx].h1, seg[idx].h2, seg[idx].len};}push(idx);int mid = (l + r) >> 1;if (qr <= mid) return qry(idx<<1, l, mid, ql, qr);if (ql > mid) return qry(idx<<1|1, mid+1, r, ql, qr);QueryRes L = qry(idx<<1, l, mid, ql, qr);QueryRes R = qry(idx<<1|1, mid+1, r, ql, qr);int llen = L.len;ll nh1 = (L.h1 + modmul(R.h1, p1[llen], MOD1)) % MOD1;ll nh2 = (L.h2 + modmul(R.h2, p2[llen], MOD2)) % MOD2;return {nh1, nh2, L.len + R.len};
}void upd(int idx, int l, int r, int ql, int qr, int v) {if (ql <= l && r <= qr) {apply_set(idx, v);return;}push(idx);int mid = (l + r) >> 1;if (ql <= mid) upd(idx<<1, l, mid, ql, qr, v);if (qr > mid) upd(idx<<1|1, mid+1, r, ql, qr, v);pull(idx);
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);if (!(cin >> n >> m >> k)) return 0;cin >> s;int ops = m + k;p1.assign(n+5, 0);p2.assign(n+5, 0);ones1.assign(n+5, 0);ones2.assign(n+5, 0);p1[0] = 1; p2[0] = 1;for (int i = 1; i <= n; ++i) {p1[i] = (p1[i-1] * 1LL * BASE) % MOD1;p2[i] = (p2[i-1] * 1LL * BASE) % MOD2;}ones1[0] = 0; ones2[0] = 0;for (int i = 1; i <= n; ++i) {ones1[i] = (ones1[i-1] + p1[i-1]) % MOD1;ones2[i] = (ones2[i-1] + p2[i-1]) % MOD2;}seg.assign(4*(n+5), Node());build(1, 1, n);for (int i = 0; i < ops; ++i) {int t; cin >> t;if (t == 1) {int l, r, c; cin >> l >> r >> c;upd(1, 1, n, l, r, c);} else {int l, r, d; cin >> l >> r >> d;int len = r - l + 1;int L = len - d;if (L <= 0) {cout << "YES\n";continue;}QueryRes a = qry(1, 1, n, l, l + L - 1);QueryRes b = qry(1, 1, n, l + d, l + d + L - 1);if (a.h1 == b.h1 && a.h2 == b.h2) cout << "YES\n";else cout << "NO\n";}}return 0;
}还有一个奇怪做法,因为memset和memcpy是1/64常数,所以...
https://www.luogu.com.cn/problem/P8147
建立AC自动机,每个询问暴力跑出来所有匹配是一个暴力。
瓶颈在于求第k大。
所以二分答案,变为查询cnt>=k的有多少个,然后check
如果用树剖暴力维护的话不行,所以我们按照关键点集合建立虚树,虚树边上的cnt都一致,这个就可以维护了。








在Elasticsearch中扮演什么角色? - 详解)










