【树状数组】codeforce 1288 E. Messenger Simulator

题目

https://codeforces.com/problemset/problem/1288/E

题解

用以下测试用例进行讲解：

4 2
3 2

上述测试用例的执行过程如图所示：

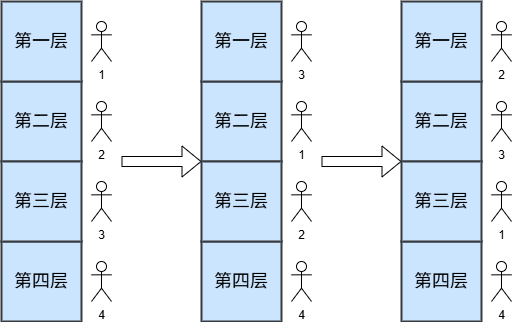
初始状态下，第 \(i\) 个人位于第 \(i\) 层，想维护的目标是每个人到达过的最高层 \(mx[i]\) 和最低层 \(mi[i]\)，显然初始时 \(mx[i] = mi[i] = i\)。

收到消息的人会上升到第一层，因此最低层只需要判断这个人有没有收到过消息或者初始时就位于第一层即可，原本在收到消息的人之上的人各自所处的楼层都会下降一层，即从第 \(x\) 层变到第 \(x + 1\) 层。

当收到第 \(3\) 个人的消息的时候，第 \(2\) 个人从原本位于第二层变为位于第三层，第 \(1\) 个人从原本位于第一层变为位于第二层，而收到消息的人，也就是第 \(3\) 个人会变为位于第一层。

随后，收到第 \(2\) 个人的消息的时候，第 \(1\) 个人从原本位于第二层变为位于第三层，第 \(3\) 个人从原本位于第一层变为位于第二层，而收到消息的人，也就是第 \(2\) 个人会变为第一层。

对于这个过程，我们容易联想到插入排序的过程是类似的，时间复杂度为 \(O(n)\) ~ \(O(n^2)\)。但是极端情况下，每次收到消息的人都是最底层的人收到消息，此时会造成数组大量的移动操作，时间复杂度为：\(O(n^2)\)，是不可接受的。有此分析，我们可以得到的启发是想解决该问题就需要避免数组大量的移动操作。

在数组不进行任何移动操作时，要做的就是将消息发送者所处楼层上面所有人的所处楼层都增加 \(1\)，然后将消息发送者直接加在楼层最上层，并且删除消息发送者原本在数组中所处位置对答案的影响，问题就转化为了以下两个子问题：

1. 如何快速为消息发送者所处楼层上面所有人的所处楼层增加 \(1\)？
2. 如何剔除收到消息的人在原来位置上对答案的影响？

为解决子问题 1，可以使用树状数组。维护三个长度为 \(n + m\) 的数组 \(a, b, tr\)，分别代表人的编号，所处楼层和树状数组，初始化时将 \(n\) ~ \(1\) 依次填入 \(a[1]\) ~ \(a[n]\) 和 \(b[1]\) ~ \(b[n]\)，其余位置初始化为 \(0\) 即可，树状数组初始化时全部填 \(0\)。随后的 \(m\) 个数依次填入 \(a[n + 1]\) ~ \(a[n + m]\)，当填入 \(a[i]（i \geq n + 1）\) 时，不妨记上一次出现值为 \(a[i]\) 的位置为 \(j\)，则需要使用树状数组将 \(j + 1\) ~ \(i\) 的每个位置都增加 \(1\)，具体的操作可以将 \(j + 1\) ~ \(n\) 的每个位置增加 \(1\)，将 \(i + 1\) 的每个位置减少 \(1\)。

为解决子问题 2，只需要将 \(a[j]\) 置为负无穷大即可。

不妨记 \(x\) 为使用树状数组计算出第 \(i\) 个位置增加了多少个 \(1\)，那么，\(b[i] + x\) 就是 \(a[i]\) 所处的楼层。当解决子问题 2 之前，需要先计算一次 \(a[j]\) 所处楼层。在所有操作都完成以后，需要再遍历一遍数组（遍历第 \(n + 1\) ~ \(n + m\) 个位置即可），计算出每个人所处过的楼层的最高层。至于每个人所处过楼层的最低层，只需要当收到那个人消息时，将其最低层更新为 \(1\) 即可，其它情况所处楼层大小只会单调不减。

参考代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;constexpr int N = 3e5 + 7;
constexpr int INF = -1e9;
int n, m, w, len;
int tr[N << 1];
int a[N << 1];
int b[N << 1];
int idx[N];
int mi[N];
int mx[N];int lowbit(int x) {return x & -x;
}void add(int idx, int val) {while (idx <= len) {tr[idx] += val;idx += lowbit(idx);}
}int sum(int idx) {int res = 0LL;while (idx > 0) {res += tr[idx];idx -= lowbit(idx);}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;len = n + m;for (int i = 1; i <= n; ++ i) a[i] = b[i] = n - i + 1, mi[i] = mx[i] = i, idx[n - i + 1] = i;for (int i = n + 1; i <= n + m; ++ i) {cin >> b[i];w = b[i];mi[w] = 1;mx[w] = max(mx[w], sum(idx[w]) + a[idx[w]]);a[idx[w]] = INF;add(idx[w] + 1, 1);add(i + 1, -1);idx[w] = i;}for (int i = 1; i <= len; ++ i) if (a[i] >= 0) mx[b[i]] = max(mx[b[i]], a[i] + sum(i));for (int i = 1; i <= n; ++ i) cout << mi[i] << ' ' << mx[i] << '\n';return 0;
}