利用耦合有限元和神经网络计算的骨重塑模拟多尺度方法

Multiscale methodology for bone remodelling simulation using coupled finite element and neural network computation

摘要：本文旨在开发一种基于有限元分析（FEA）和神经网络（NN）计算的多尺度分层混合模型，通过将介观尺度（骨小梁网络层级）与宏观尺度（全骨层级）耦合，模拟骨重建过程。由于全骨模拟（包括骨小梁层级的3D重建）耗时巨大，本研究仅在宏观层面进行有限元计算，而通过训练的神经网络替代介观尺度所需的有限元代码，以快速预测骨小梁的形态与力学适应性。宏观尺度的骨力学属性根据介观尺度神经网络计算的形态与力学适应性结果进行更新。基于μ-CT影像的数字化建模技术和体素有限元分析被用于捕捉股骨头介观尺度下2 mm³的代表性体积元（RVE）。人工神经网络的输入数据包括骨材料参数、边界条件及施加的应力，输出数据为更新后的骨属性（如弹性模量）和骨小梁参数（如体积分数）。据我们所知，这是首个结合有限元分析与神经网络计算、快速模拟多层级骨适应性变化的模型。
核心目标：
开发多尺度耦合模型（宏观FEA + 介观NN），解决传统全骨模拟（含骨小梁3D重建）计算成本高的问题，实现骨重建过程的高效跨尺度仿真。
方法框架：

宏观尺度：利用有限元法（FEA）模拟全骨力学响应，获取应力/应变分布及边界条件。
介观尺度：通过μ-CT影像构建2 mm³代表体积元（RVE），训练神经网络（输入：材料参数、边界条件、应力；输出：更新骨属性及骨小梁参数），替代传统三维FEA，快速预测骨小梁网络的适应性变化。
双向耦合：宏观FEA将力学状态传递至介观NN，NN预测微结构响应后反馈更新宏观材料属性，形成闭环优化。

技术创新：

首次耦合FEA与NN：突破传统多尺度模拟依赖单一方法的局限，利用NN加速介观计算（耗时从小时级降至秒级）。
数据驱动建模：基于μ-CT影像提取真实骨小梁微结构，结合体素有限元生成训练数据，提升模型生物学真实性。
动态属性更新：通过NN实时修正宏观骨属性（如弹性模量、密度），反映骨重建的适应性机制。

应用价值：

高效性：显著降低计算成本，支持临床场景（如骨质疏松治疗规划、植入物设计）中的快速力学评估。
多尺度预测能力：同时捕捉全骨宏观力学响应与骨小梁介观结构演变，为骨适应性机制研究提供新工具。
可扩展性：框架可推广至其他生物组织（如软骨、血管）的多尺度力学建模。

潜在挑战：

数据依赖：NN性能受限于μ-CT数据质量与多样性，需大规模标注数据集。
模型可解释性：NN的“黑箱”特性可能限制其在临床决策中的可信度。
三维扩展：当前宏观FEA为二维简化模型，未来需扩展至三维全骨仿真以提升精度。

1 引言

骨骼是一种分层组织的材料，其适应性在很大程度上取决于其小梁结构，随着时间的推移可以通过对其形态和机械性能的变化进行评估（Tovar 2004; Yoo 和 Jasiuk 2006）。2004年，Poter 提出了用于骨骼的多尺度建模的分析方案，将其视为一种天然混合纳米复合材料，以预测组成材料的个体特性。尽管所提出的模型对皮质骨的杨氏模量给出了与现有实验数据良好的估计，但它无法提供关于应力分布和骨微结构演变的数据。Sansalone 等（2007）使用了一种二维多尺度建模方法来研究骨骼的机械性能。他们的方法提供了在给定尺度上的机械响应。Ghanbari 和 Naghdabadi（2009）采用了一种分层多尺度建模方案分析皮质骨，认为其是一种纳米复合材料。定义了一个宏观尺度和一个微观尺度的边界值问题。通过采用均匀化技术在这些尺度之间建立耦合。尽管在骨骼多尺度建模领域取得了进展，但仍缺乏整合不同尺度的骨结构信息及重塑过程的模型（Viceconti 等，2008）。骨重塑过程的计算模型必须解决多层次上的骨结构变化，从而允许对整块骨骼进行更准确的描述（Adachi 等，1999; Fernandes 等，1999; Bagge 2000; Huiskes 等，2000; McNamara 和 Prendergast，2007; Hambli 等，2009）。该过程以分层方式在不同的时间和空间尺度上发生，交互现象连接着不同的尺度（Weiner 和 Traub，1992; Rho 等，1998; Tovar 2004; Yoo 和 Jasiuk 2006）。近年来，提出了多种数学模型来解释和模拟重塑过程。虽然这些模型提供了有价值的见解，但到目前为止，它们仅通过基于理想化的二维或三维小梁结构的均匀化方法来解决骨结构/属性的变化（Adachi 等，1998, 1999; Yoo 和 Jasiuk 2006; Fernandes 等，1999; Bagge 2000; Jacobs 2000; Sansalone 等，2007）。此外，在各种多尺度建模方法中，分层多尺度建模方法比均匀化方法在确定各个层次间相互作用方面更具优势。最近，Leardini 等（2006），Viceconti 等（2007, 2008）开发了一种解剖功能多尺度超级模型，用于人类肌肉骨骼系统，能够预测在常规物理负荷下的骨折风险。他们引入了一种随机本构律来表示骨材料响应相对于位置和时间的变化。所提出的超级模型被构思为五个相互依赖的子模型的相互连接：连续性、边界条件、本构方程、重塑历史和失效标准。整个解剖功能超级模型被定义为一组程序化宏，用于预测特定个体的骨折风险。该模型的应用复杂，因为其基于对子模型的串行执行。此外，尚未提出将各个子模型集成到单一阶段执行中的方案，这使得其在日常临床使用中的应用既冗长又耗时。Jang 和 Kim（2010）开发了一种数值框架，计算确定骨重塑过程中皮质和小梁骨类型的相互作用和结构变化。他们构建了一种二维微有限元（μFE）模型，代表人类近端股骨的整个皮质骨和总小梁架构。研究的一个限制是，考虑了在介观级别上的二维适应，因此无法捕捉到骨重塑过程的真实三维特性。

在本文中，我们描述了一种快速的多尺度方法，用于模拟骨重塑过程，采用二维有限元（FE）分析在宏观层面，三维神经网络（NN）计算在介观层面。我们区分以下结构层次：宏观结构（整体骨骼）和介观结构（小梁架构）。从数值角度来看，组织（宏观）尺度通过在每个有限元网格上求解宏观分析后获得的宏观变量和边界条件，将信息传递到介观尺度。在介观尺度上，将宏观有限元结果得出的局部边界条件应用于介观骨模型，并通过训练的神经网络计算介观模型响观尺度将信息应。最后，介以更新后的材料性质的形式回传给宏观尺度。

我们使用数字图像建模技术，通过μ-CT和体素有限元分析，在股骨头的介观水平上捕获代表性体积元素（RVE）为2 mm³。人工神经网络的输入数据是一组骨材料参数、边界条件和施加的应力。输出数据是更新后的骨属性和一些小梁骨因子。当复杂模型的数值分析耗时或不可行时，NN方法非常有用（Topping 和 Bahreininejad 1992; Jenkins 1997; Rafiq 等，2001; Unger 和 Konke 2008; Hambli 等，2006）。此外，NN模型可以用于整合从实验数据和医学图像中提取的信息。该方法的另一个优点是，不同尺度之间的联接阶段以及逆计算的应用可以快速且轻松地进行（Jenkins 1997; Rafiq 等，2001）。

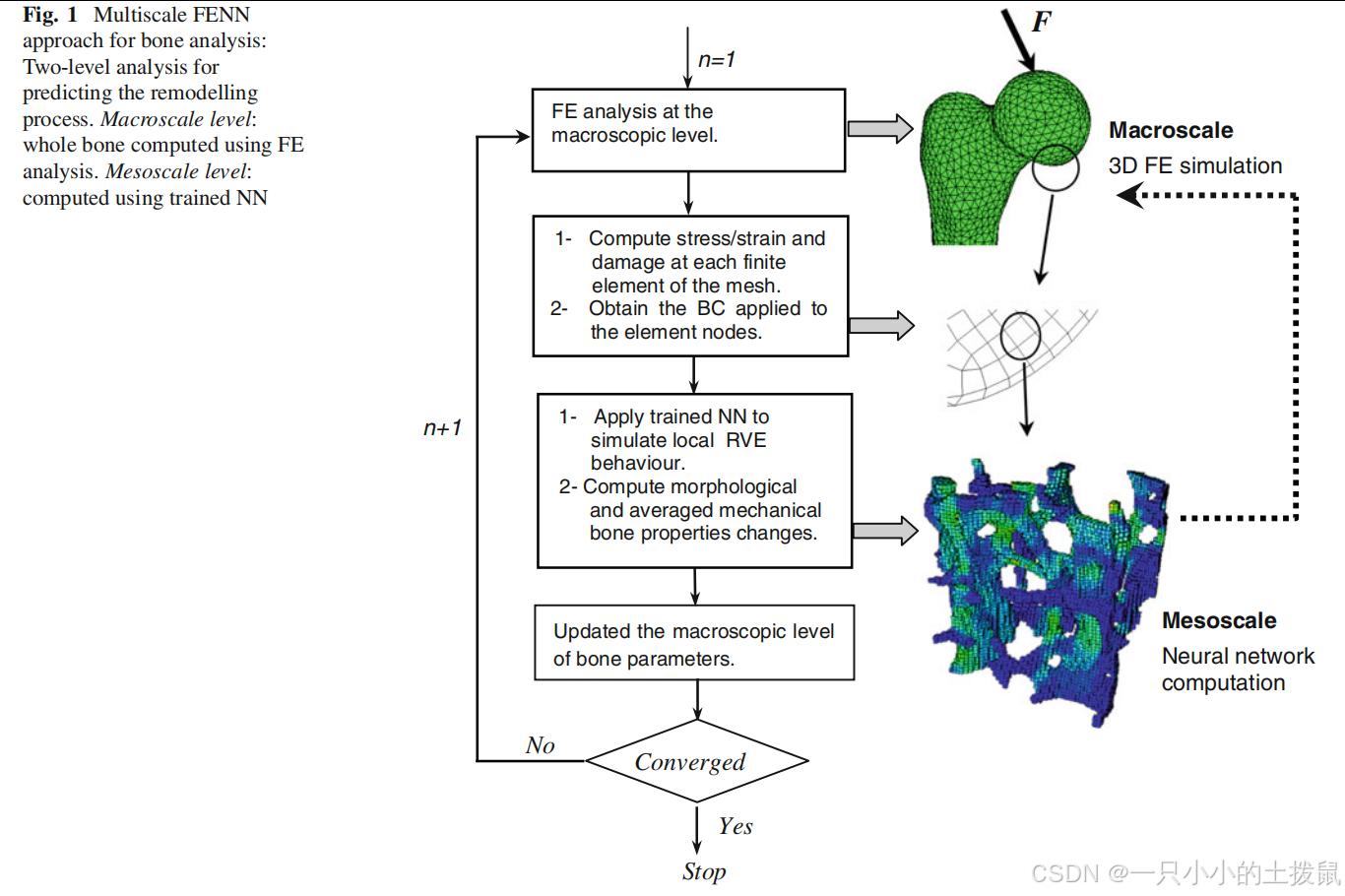
2 方法

提出的“混合有限元与神经网络”（FENN）方法是一种模拟程序，其中将骨骼的连续体模型离散化为更小的子模型。经过训练的神经网络（NN）局部应用于确定小梁网络中的任何结构和机械变化。然后将局部结果反馈到全局水平模型中。连续体模型的材料分布变化将影响应力和应变场的分布，从而影响后续迭代中每个介观模型的机械刺激。FENN方法的示意图如图1所示。

在本研究中，介观尺度的研究基于以40μm体素大小获取的2 mm³均匀代表性体积元素（RVE）样品的计算微位扫描（图2）。介观方法可以总结为以下五个步骤：

针对不同组合的骨输入进行RVE的有限元重塑模拟。
对RVE输出进行平均。
步骤1和2提供以“实验设计”（DoE）表格形式的训练数据，用于NN训练。
基于数字DoE对NN进行训练。
将NN纳入宏观有限元模型，以链接介观和宏观尺度。

方法概述

FENN 方法：结合有限元分析（FE）与神经网络（NN）来模拟骨骼结构的重塑过程。
模型离散化：将连续体骨模型分解为更小的子模型，便于局部分析。

核心步骤

有限元重塑模拟：对不同的骨输入组合进行模拟，生成代表性体积元素（RVE）。
输出平均化：对各个RVE的模拟结果进行平均处理。
训练数据准备：生成实验设计（DoE）表，为神经网络的训练提供数据。
神经网络训练：基于前面步骤得到的数字DoE，对神经网络进行训练。
模型集成：将经过训练的神经网络整合进宏观有限元模型，以实现介观与宏观尺度之间的关联。

研究数据来源

微位扫描：基于40μm体素大小的计算微位图像，获取2 mm³的均匀RVE样品。

2.1宏观尺度的有限元模型

模型中包含三种不同材料：骨小梁（松质骨）、皮质骨（密质骨）和骨髓。然而，与骨基质相比，骨髓的力学影响可忽略不计（Martínez-Reina等，2009）。
从结构上看，骨组织是一种具有复杂层级结构的复合材料。在连续介质层面，骨的有效力学性能取决于其结构，因此表现出各向异性行为。对于皮质骨，其孔隙率极低，各向异性主要由骨板层和骨单位方向控制；对于松质骨，孔隙率较高，各向异性的主要决定因素是骨小梁的取向。已有研究提出了多种各向异性本构模型以模拟骨的行为（Jacobs等，1997；Hart和Fritton，1997；Fernandes等，1999；Doblare和Garcia，2002；Martínez-Reina等，2009）。由于本研究聚焦宏观尺度，为简化计算，采用平均化的各向同性骨行为模型（Tovar，2004）。未来工作需扩展模型以纳入各向异性和骨髓的影响。

宏观尺度下皮质骨与松质骨的本构方程表示为：

其中，σij为应力，εkl为应变，aijkl为各向同性弹性刚度张量。
宏观模型中未考虑损伤效应，其耦合作用通过介观尺度（骨小梁层级）的公式引入。此外，本研究未涉及皮质骨的重建过程，但宏观有限元模型未来可扩展以描述皮质骨和松质骨的重建机制。

材料组成与简化假设

材料类型：模型包含骨小梁（松质骨）、皮质骨（密质骨）和骨髓，但忽略骨髓的力学贡献。
简化处理：在宏观尺度下，假设骨为各向同性材料（忽略实际各向异性），以降低计算复杂度。

骨结构的各向异性特征

皮质骨：低孔隙率（<10%），各向异性由骨板层排列和骨单位方向主导。
松质骨：高孔隙率（50-90%），各向异性由骨小梁网络取向决定。

宏观本构模型

本构方程：采用线性弹性各向同性模型（式1），弹性刚度张量aijkl由平均化材料参数定义。
局限性：当前模型未考虑骨重建引起的材料非线性（如塑性变形或黏弹性效应）。

损伤与重建的跨尺度处理

损伤机制：损伤仅在**介观尺度（骨小梁层级）**引入，通过微结构失效（如骨小梁断裂）影响宏观力学响应。
重建过程：当前模型仅模拟松质骨重建，未来需扩展至皮质骨。

2.2 用于神经网络训练的介观尺度有限元模型

骨小梁的有效力学特性被建模为弹性各向同性行为，并耦合了应变与微损伤刺激的损伤机制（McNamara和Prendergast，2007）。其本构关系表示为：
σij=(1−D)aijklεkl(2)
其中，aijkl 为各向同性弹性刚度张量。
对于纯弹性应变下的高周疲劳问题（忽略热耗散与机械耗散的耦合），Chaboche（1981）提出了非线性损伤模型：
D=1−(1−(NfN)1−α1)1+β1(3)
式中，α 和 β 为材料参数，Nf 为失效循环次数，由Martin等（1998）提出的公式确定：
Nfc=1.479×10−21Δε−10.3（压缩载荷）(4a)
Nft=3.630×10−32Δε−14.1（拉伸载荷）(4b)
其中，Δε 为施加的微应变幅值。
骨密度的动态变化由以下方程组描述（Hambli等，2009）：
dtdρ=αR(S−SR)若 S<SR(5a)
dtdρ=0若 SR≤S≤SF(5b)
dtdρ=αF(S−SF)若 SF<S<SD(5c)
dtdρ=αD(S−SD)若 S≥SD(5d)
式中，ρ 为骨密度，t 为时间，S 为应变-损伤耦合刺激函数；αR、αF 和 αD 分别表示骨吸收速率、骨形成速率和损伤吸收速率；SR、SF 和 SD 分别为骨吸收、骨形成和损伤吸收的刺激阈值。
刺激函数 S 由骨细胞力学感知模型定义（Mullender和Huiskes，1995）：
S(x,t)=i=1∑Nocfi(x)μiSi(6)
其中，μi 为骨细胞 i 的机械敏感性，Noc 为骨细胞数量；fi(x) 为空间影响函数：
fi(x)=exp(−d0di(x))(7)
式中，di(x) 为骨细胞 i 与骨表面位置 x 的距离，d0 为归一化因子。局部刺激值 Si 由应变-损伤能量密度定义（Hambli等，2009）：
S=21ρ(1−D)σijεij(8)
骨密度的更新通过前向欧拉法近似：
ρit+Δt=ρit+Δρi(9)
局部弹性模量 E 由下式计算（Hambli等，2009）：
E=C(1−D)ργ(10)
式中，C 和 γ 为实验标定常数。
代表体积元（RVE）的输出变量通过体积平均化处理（Ghanbari和Naghdabadi，2009）：
yiRVE=V01∫VOyidV(11)
其中，V0 为RVE参考域体积，yi 为每个有限元位置的输出变量。