【LeetCode】升级打怪之路 Day 24：回溯算法的解题框架

今日题目：

46. 全排列
51. N 皇后
78. 子集

LC 46. 全排列

46. 全排列

学会回溯算法的思路后，这个题目就不难了，看看解题框架是如何运用到这个题目中的：

class Solution {private List<List<Integer>> result;private void backtrack(List<Integer> path, int[] nums, boolean[] used) {// 加入结果集if (path.size() == nums.length) {result.add(new ArrayList<>(path));}// 遍历选择for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}// 做出选择used[i] = true;int num = nums[i];path.addLast(num);backtrack(path, nums, used);// 撤销选择used[i] = false;path.removeLast();}}public List<List<Integer>> permute(int[] nums) {result = new ArrayList<>();List<Integer> path = new ArrayList<>();boolean[] used = new boolean[nums.length];Arrays.fill(used, false);backtrack(path, nums, used);return result;}
}

LC 51. N 皇后

51. N 皇后

这也是经典的使用回溯来解题的题目：每一次在新的一行中选出一列放上棋子，直到 n 行都放上棋子后就可以作为一种答案。

这个题目在使用回溯算法时，关键难点在于如何判断在做出一个选择后的棋局是否满足 N 皇后要求。因为我们是每次在新的一行中放入棋子，所以只需要检测这个新的棋子是否存在列冲突以及斜线冲突。

按照以上思路，题目也就不难了。

LC 78. 子集【classic】

78. 子集

这个题目有两种思路来画回溯算法的决策树：

1）思路一

在这里插入图片描述

每一次做选择时，是从当前节点元素在 nums 后面的元素中选一个加入到路径中。在遍历这个决策树时，每一步都将其加入到结果集中，就可以得到所有的子集了。

2）思路二

决策树的第 i 层所做的选择是：nums[i] 是否使用。然后叶子节点就对应了一个结果集中的答案。决策树如下：

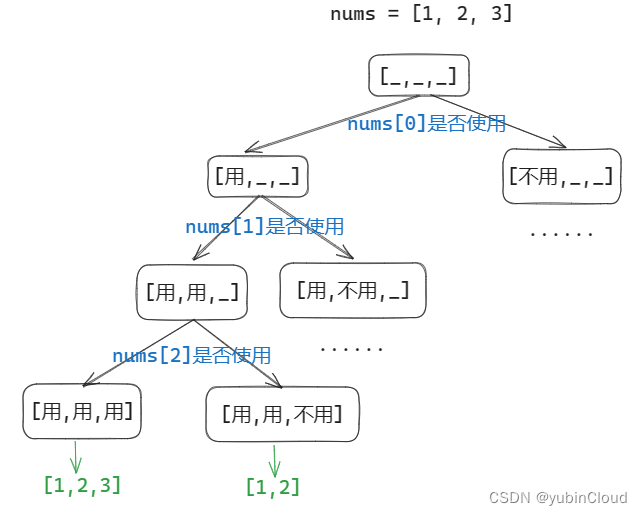
在这里插入图片描述

这里看一下两种思路的代码：

思路一代码：

class Solution {private List<List<Integer>> result;private static List<Boolean> choices = List.of(false, true);private void backtrace(List<Integer> path, int[] nums, int start) {result.add(new ArrayList<>(path));for (int i = start; i < nums.length; i++) {path.addLast(nums[i]);backtrace(path, nums, i + 1);path.removeLast();}}public List<List<Integer>> subsets(int[] nums) {result = new ArrayList<>();backtrace(new ArrayList<>(), nums, 0);return result;}
}

思路二代码：

class Solution {private List<List<Integer>> result;private static List<Boolean> choices = List.of(false, true);private void backtrace(List<Integer> path, int[] nums, int level) {if (level == nums.length) {result.add(new ArrayList<>(path));return;}// 遍历选择列表for (var choice: choices) {int num = nums[level];if (choice) {path.addLast(num);backtrace(path, nums, level + 1);path.removeLast();} else {backtrace(path, nums, level + 1);}}}public List<List<Integer>> subsets(int[] nums) {result = new ArrayList<>();if (nums.length == 0) {return List.of(Collections.emptyList());}backtrace(new ArrayList<>(), nums, 0);return result;}
}