1.冒泡排序
1.1 冒泡排序普通版
每次冒泡过程都是从数列的第一个元素开始,然后依次和剩余的元素进行比较,若小于相邻元素,则交换两者位置,同时将较大元素作为下一个比较的基准元素,继续将该元素与其相邻的元素进行比较,直到数列的最后一个元素 .(最后的元素最大,也是最先固定)
import java.util.Arrays;public class BubbleSort {public static void main(String[] args) {int[] arr = new int[]{9, 2, 1, 0, 5, 3, 6, 4, 8, 7};System.out.println("排序前:" + Arrays.toString(arr));sort(arr);System.out.println("排序后:" + Arrays.toString(arr));}// 冒泡排序方法public static void sort(int[] arr) {// 第一层for循环,用来控制冒泡的次数for (int i = 1; i < arr.length; i++) {// 第二层for循环,用来控制冒泡一层层到最后for (int j = 0; j < arr.length - 1; j++) {// 如果前一个数比后一个数大,两者调换,意味着泡泡向上走了一层if (arr[j] > arr[j + 1]) {int temp = arr[j]; // 临时变量temp用来交换两个数值arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
}运行结果:
排序前:[9, 2, 1, 0, 5, 3, 6, 4, 8, 7]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
1.2 冒泡排序升级版
在这个版本中,改动了两点 . 第一点是加入了一个布尔值,判断第二层循环中的调换有没有执行,如果没有进行两两调换,说明后面都已经排好序了,已经不需要再循环了,直接跳出循环,排序结束 ; 第二点是第二层循环不再循环到arr.length - 1,因为外面的i循环递增一次,说明数组最后就多了一个排好序的大泡泡.第二层循环也就不需要到最末尾一位了,可以提前结束循环
/**
-
升级版冒泡排序:
-
加入一个布尔变量,如果内循环没有交换值,说明已经排序完成,提前终止
*/
import java.util.Arrays;public class BubbleSort {public static void main(String[] args) {int[] arr = new int[]{9, 2, 1, 0, 5, 3, 6, 4, 8, 7};System.out.println("排序前:" + Arrays.toString(arr));plusSort(arr);System.out.println("排序后:" + Arrays.toString(arr)); }// 升级版冒泡排序方法public static void plusSort(int[] arr) {if (arr != null && arr.length > 1) {for (int i = 0; i < arr.length - 1; i++) {// 初始化一个布尔值,用于标记此次循环内是否进行了交换操作boolean flag = true;for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]与arr[j+1]的值int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;// 改变flag的值,表示进行了交换操作flag = false;}}// 如果flag为true,表示在此次循环中没有进行交换操作,即已经完成了排序,提前终止外层循环if (flag) {break;}}}}
}运行结果:
排序前:[9, 2, 1, 0, 5, 3, 6, 4, 8, 7]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
2.选择排序
选择排序也是一种简单直观的排序算法,实现原理比较直观易懂:首先在未排序数列中找到最小元素,然后将其与数列的首部元素进行交换,然后,在剩余未排序元素中继续找出最小元素,将其与已排序数列的末尾位置元素交换。以此类推,直至所有元素都排序完毕
/**
-
选择排序:
-
每一次从待排序的数据元素中选出最小(或最大)的一个元素,
-
存放在序列的起始位置,直到全部待排序的数据元素排完。
*/
import java.util.Arrays;public class SelectSort {public static void main(String[] args) {int[] arr = new int[] {3, 4, 5, 7, 1, 2, 0, 9, 3, 6, 8}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组selectSort(arr); // 调用选择排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}// 选择排序方法public static void selectSort(int[] arr) {// 外层循环控制当前需要进行比较的元素索引位置for (int i = 0; i < arr.length - 1; i++) {int minIndex = i; // 设定当前循环的起始位置为最小值的位置// 内层循环寻找未排序部分中的最小值的索引for (int j = i + 1; j < arr.length; j++) {if (arr[minIndex] > arr[j]) {minIndex = j; // 如果当前位置的值比起始位置的值小,则更新最小值的索引}}// 如果找到最小值的索引与当前循环位置不同,则交换两个位置的值,将最小值交换至当前位置if (i != minIndex) {int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}}
}运行结果:
排序前:[3, 4, 5, 7, 1, 2, 0, 9, 3, 6, 8]
排序后:[0, 1, 2, 3, 3, 4, 5, 6, 7, 8, 9]
3.插入排序
一次插入排序的操作过程:将待插元素,依次与已排序好的子数列元素从后到前进行比较,如果当前元素值比待插元素值大,则将移位到与其相邻的后一个位置,否则直接将待插元素插入当前元素相邻的后一位置,因为说明已经找到插入点的最终位置(类似于打牌)
/**
-
插入排序:
-
从第一个元素开始,该元素可以认为已经被排序
-
取出下一个元素,在已经排序的元素序列中从后向前扫描
-
如果该元素(已排序)大于新元素,将该元素移到下一位置
-
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
-
将新元素插入到该位置后
-
重复上面步骤
*/
import java.util.Arrays;public class InsertSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组insertSort(arr); // 调用插入排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}// 插入排序方法public static void insertSort(int[] arr) {// 外层循环控制插入的元素索引位置for (int i = 1; i < arr.length; i++) {int temp = arr[i]; // 保存当前需要插入的元素值int j;// 内层循环比较并将元素插入到正确的位置for (j = i - 1; j >= 0 && temp < arr[j]; j--) {arr[j + 1] = arr[j]; // 将元素往后移动}arr[j + 1] = temp; // 将当前元素插入到正确位置}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
4.快速排序
快速排序算法利用的是一趟快速排序,基本内容是选择一个数作为准基数,然后利用这个准基数将遗传数据分为两个部分,第一部分比这个准基数小,都放在准基数的左边,第二部分都比这个准基数大,放在准基数的右边.
import java.util.Arrays;
/**
-
快速排序:
-
快速排序算法利用的是一趟快速排序,基本内容是选择一个数作为准基数,
-
然后利用这个准基数将遗传数据分为两个部分,第一部分比这个准基数小,
-
都放在准基数的左边,第二部分都比这个准基数大,放在准基数的右边.
*/
public class QuickSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组quickSort(arr, 0, arr.length - 1); // 调用快速排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 快速排序方法* @param arr 待排序的数组* @param begin 排序起始位置* @param end 排序结束位置*/public static void quickSort(int[] arr, int begin, int end) {// 递归终止条件:起始位置大于等于结束位置if (begin >= end) {return;}int pivot = arr[begin]; // 选择基准元素,默认以第一个元素为基准int left = begin + 1; // 左边起始位置int right = end; // 右边结束位置while (left <= right) {/*** 在左边找到第一个大于基准元素的位置* 注意:这里要先判断left <= right,否则会导致索引越界*/while (left <= right && arr[left] <= pivot) {left++;}/*** 在右边找到第一个小于基准元素的位置* 注意:这里要先判断left <= right,否则会导致索引越界*/while (left <= right && arr[right] >= pivot) {right--;}// 如果左指针仍在右指针左边,则交换左、右指针所指的元素if (left < right) {swap(arr, left, right);}}// 将基准元素交换到正确的位置,即左指针所在位置swap(arr, begin, right);// 对左边部分进行快速排序quickSort(arr, begin, right - 1);// 对右边部分进行快速排序quickSort(arr, right + 1, end);}/*** 交换数组中两个元素的位置* @param arr 数组* @param i 第一个元素的索引* @param j 第二个元素的索引*/public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
5.归并排序
归并排序,简单的说把一串数,从中平等分为两份,再把两份再细分,直到不能细分为止,这就是分而治之的分的步骤. 再从最小的单元,两两合并,合并的规则是将其按从小到大的顺序放到一个临时数组中,再把这个临时数组替换原数组相应位置
import java.util.Arrays;
/**
-
归并排序:
-
归并操作的工作原理如下:
-
第一步:申请空间,使其大小为两个已经 排序序列之和,该空间用来存放合并后的序列
-
第二步:设定两个 指针,最初位置分别为两个已经排序序列的起始位置
-
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置重复步骤3直到某一指针超出序列尾
-
将另一序列剩下的所有元素直接复制到合并序列尾
*
*/
public class MergeSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组mergeSort(arr, 0, arr.length - 1); // 调用归并排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 归并排序方法* @param a 待排序的数组* @param s 排序起始位置* @param e 排序结束位置*/public static void mergeSort(int[] a, int s, int e) {if (s < e) {int m = (s + e) / 2; // 找到数组的中间位置mergeSort(a, s, m); // 递归调用对左边部分进行归并排序mergeSort(a, m + 1, e); // 递归调用对右边部分进行归并排序merge(a, s, m, e); // 合并左右两个有序数组}}/*** 合并左右两个有序数组* @param a 原始数组* @param s 左数组起始位置* @param m 左数组结束位置* @param e 右数组结束位置*/private static void merge(int[] a, int s, int m, int e) {int[] temp = new int[e - s + 1]; // 临时数组用来存放合并后的结果int l = s; // 左数组的起始位置int r = m + 1; // 右数组的起始位置int i = 0; // 临时数组的索引// 比较左右两个数组中的元素,将较小的元素放入临时数组中while (l <= m && r <= e) {if (a[l] < a[r]) {temp[i++] = a[l++];} else {temp[i++] = a[r++];}}// 将左数组中剩余的元素放入临时数组中while (l <= m) {temp[i++] = a[l++];}// 将右数组中剩余的元素放入临时数组中while (r <= e) {temp[i++] = a[r++];}// 将临时数组中的元素覆盖原始数组中的元素,完成排序for (int n = 0; n < temp.length; n++) {a[s + n] = temp[n];}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
6.希尔排序
当数组规模较大时,插入排序的效率较低。希尔排序(Shell Sort)是一种插入排序的改进算法,通过将相隔一定间隔的元素进行分组,对每个分组进行插入排序,逐步缩小间隔,最终完成排序。
具体步骤如下:
1. 首先,选定一个初始的间隔值(称为步长),通常将数组长度的一半作为初始值。
2. 根据选定的步长,将数组分成若干个分组。
3. 对每个分组进行插入排序,即将每个分组中的元素按照插入排序的方式进行排序。
4. 缩小步长,继续第2和第3步操作,直到步长为1。
5. 当步长为1时,进行最后一次插入排序,此时数组已经基本有序,插入排序的效率会很高。
希尔排序的关键在于选定合适的步长和分组方式。常用的步长序列有希尔原始提出的递减系列(n/2, n/4, n/8...),以及Hibbard系列(2^k - 1, 2^(k-1) - 1...),Sedgewick系列等。
希尔排序的时间复杂度与步长序列的选取有关,最好的情况下为O(n^(3/2)),平均情况下为O(nlogn)。希尔排序是一种不稳定的排序算法,即相同元素的相对顺序在排序后可能发生变化。
希尔排序相对于插入排序来说,虽然没有改变算法的基本思想,但通过拆分成多个子序列进行插入排序,大大提高了排序的效率。
import java.util.Arrays;public class ShellSort {public static void main(String[] args) {int[] arr = new int[] {5, 3, 2, 8, 4, 9, 1, 0, 7, 6}; // 待排序的数组System.out.println("排序前:" + Arrays.toString(arr)); // 输出排序前的数组shellSort(arr); // 调用希尔排序方法System.out.println("排序后:" + Arrays.toString(arr)); // 输出排序后的数组}/*** 希尔排序方法* @param arr 待排序的数组*/public static void shellSort(int[] arr) {int gap = arr.length / 2; // 初始步长int k = 1; // 记录排序轮数// 根据步长进行分组,对每个分组进行插入排序while (gap > 0) {// 对每个分组进行插入排序for (int i = gap; i < arr.length; i++) {// 对当前分组的元素进行插入排序for (int j = i - gap; j >= 0; j -= gap) {if (arr[j] > arr[j + gap]) {// 如果前一个元素大于后一个元素,则进行交换int temp = arr[j];arr[j] = arr[j + gap];arr[j + gap] = temp;}}}System.out.println("第" + k++ + "轮排序结果:" + Arrays.toString(arr));gap /= 2; // 缩小步长}}
}运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
[5, 1, 0, 7, 4, 9, 3, 2, 8, 6]
[0, 1, 3, 2, 4, 6, 5, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
7.基数排序
基数排序(Radix Sort)是一种非比较性的稳定排序算法,它将整数按照每个位上的数字进行排序,可以根据位数进行排序,依次按个位、十位、百位...从低位到高位进行排序。基数排序适用于排序非负整数或具有相同位数的正整数序列。
具体步骤如下:
1. 找到数组中的最大值,并确定最大值的位数,作为排序的轮数。
2. 从个位开始,根据当前位上的数字将元素分配到对应的桶中。
3. 按照分配的顺序重新排列数组。
4. 继续处理十位、百位...直到处理完最高位,完成排序。
基数排序要求具备一定的稳定性,即在同一位上相同数字的先后顺序不发生改变。
以下是带有详细注释的基数排序的Java代码示例:```java
import java.util.*;public class RadixSort {public static void radixSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}// 获取数组中的最大值int max = Arrays.stream(arr).max().getAsInt();// 计算最大值的位数,决定排序的轮数int exp = 1;while (max / exp > 0) {countingSort(arr, exp);exp *= 10;}}// 对数组按照某一位上的值进行计数排序private static void countingSort(int[] arr, int exp) {int n = arr.length;int[] output = new int[n];int[] count = new int[10];// 统计该位上每个数字的出现次数for (int num : arr) {count[(num / exp) % 10]++;}// 将计数数组转换为位置索引数组for (int i = 1; i < 10; i++) {count[i] += count[i - 1];}// 按照该位上的值将元素放入output数组中for (int i = n - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 将排序好的数组赋值给原数组System.arraycopy(output, 0, arr, 0, n);}public static void main(String[] args) {int[] arr = {170, 45, 75, 90, 802, 24, 2, 66};System.out.println("排序前:" + Arrays.toString(arr));radixSort(arr);System.out.println("排序后:" + Arrays.toString(arr));}
}这段代码实现了带有详细注释的基数排序算法。在基数排序过程中,首先找到数组中的最大值,然后逐个按位进行计数排序。最后,将排序好的数组赋值给原数组。基数排序的时间复杂度为O(d*(n+b)),其中d为最大值的位数,n为数组长度,b为基数(这里是10)。基数排序是一种稳定的排序算法,适用于整数排序。
运行结果:
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
8.堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点
堆排序(Heap Sort)是一种基于完全二叉树数据结构——堆的排序算法,它利用堆的性质进行排序。堆排序首先将待排序的元素构建成一个最大堆(或最小堆),然后将堆顶元素与堆尾元素交换,调整剩余元素重新构建堆,重复这个过程直到所有元素都有序。堆排序的时间复杂度为O(nlogn),具有原址排序的特点,是不稳定排序算法。
具体步骤如下:
1. 构建最大堆(大顶堆):从最后一个非叶子节点开始,向上逐个调整节点,保证父节点的值大于等于子节点的值。
2. 调整堆:交换堆顶元素与最后一个元素,然后将剩余元素重新构建最大堆。
3. 重复步骤2,直到所有元素有序。
4. 如果要实现升序排序,则采用大顶堆;如果要实现降序排序,则采用小顶堆。
以下是带有详细注释的堆排序的Java代码示例:```java
public class HeapSort {public static void heapSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int n = arr.length;// 构建最大堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 调整堆结构,交换堆顶元素与末尾元素for (int i = n - 1; i >= 0; i--) {// 交换堆顶元素和末尾元素int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 调整堆heapify(arr, i, 0);}}// 调整堆private static void heapify(int[] arr, int n, int i) {int largest = i; // 最大元素的下标int left = 2 * i + 1; // 左子节点下标int right = 2 * i + 2; // 右子节点下标// 左子节点大于根节点if (left < n && arr[left] > arr[largest]) {largest = left;}// 右子节点大于根节点if (right < n && arr[right] > arr[largest]) {largest = right;}// 如果最大元素不是根节点,交换根节点和最大元素if (largest != i) {int temp = arr[i];arr[i] = arr[largest];arr[largest] = temp;// 继续调整堆heapify(arr, n, largest);}}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6, 7};System.out.println("排序前:" + Arrays.toString(arr));heapSort(arr);System.out.println("排序后:" + Arrays.toString(arr));}
}
```
这段代码实现了带有详细注释的堆排序算法。在堆排序过程中,首先构建最大堆,然后将堆顶元素与末尾元素交换,调整剩余元素重新构建最大堆。重复这个过程直到所有元素有序。堆排序的时间复杂度为O(nlogn),是一种高效的排序算法。
运行结果
排序前:[5, 3, 2, 8, 4, 9, 1, 0, 7, 6]
排序后:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
各种算法的比较

归并排序空间复杂度是O(n)
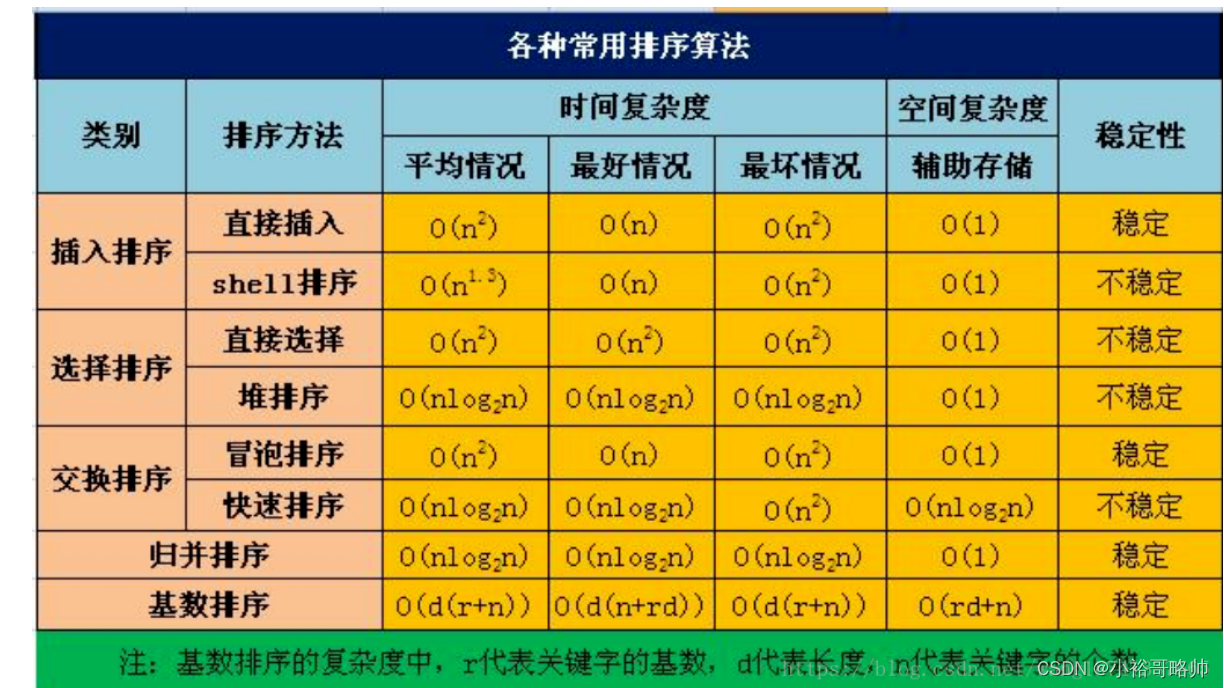
速度: 快速排序>>归并排序>>>>>插入排序>>选择排序>>冒泡排序
并且可以看到,选择排序,冒泡排序在数据量越来越大的情况下,耗时已经呈指数型上涨,而不是倍数上涨
(1)若n较小(如n≤50),可采用直接插入或直接选择排序。
当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插人,应选直接选择排序为宜。
(2)若文件初始状态基本有序(指正序),则应选用直接插人、冒泡或随机的快速排序为宜;
(3)若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
快速排序是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
若要求排序稳定,则可选用归并排序。
















![pwn旅行之[NISACTF 2022]ezpie](http://pic.xiahunao.cn/pwn旅行之[NISACTF 2022]ezpie)


