🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022
目录
一.计数排序简介及思想
二.计数排序代码实现
三.计数排序复杂度分析
📌时间复杂度
📌空间复杂度
结语
一.计数排序简介及思想
计数排序(Counting Sort)又称为鸽巢原理,是对哈希直接定址法的变形应用.
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
算法动图演示如下:
计数排序的实现思路:
- 统计每个数据出现的次数
- 按序输出
虽然计数排序实现思路比较简单,但我们还是有一些细节需要注意:
绝对映射和相对映射:
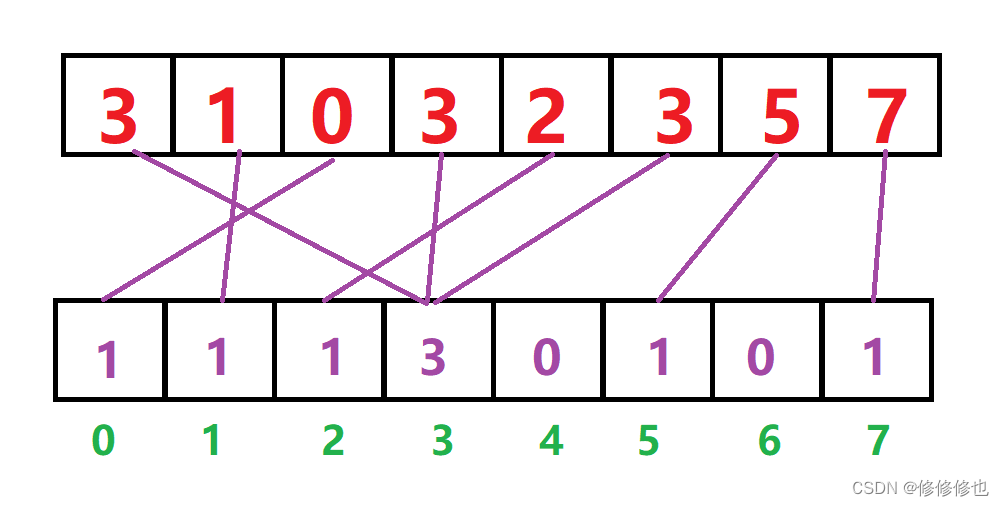
- 绝对映射:如下图,数据的数值和数组下标是一一对应的,这种计数方式叫做绝对映射
- 绝对映射的缺点:开辟数组占用空间大,不能够排负数
- 相对映射:如下图,数据在数组中是按照数值的相对大小来映射的,这种计数方式叫做相对映射.
相对映射较好的解决了绝对映射的缺点,但当遇到待排数据分布较为分散且跨度较大时,就不太适合使用计数排序来进行排序了.
二.计数排序代码实现
算法实现步骤:(以升序为例)
- 遍历待排数组,找出数组中的最大值max和最小值min.
- 开辟大小为max-min+1大小的数组用以计数.
- 遍历数组计数.
- 将计数数组中记录的数据恢复到原数组中.
综上,计数排序的代码实现如下:
//计数排序
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 1; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;int* countA = (int*)calloc(sizeof(int) , range);if (countA == NULL){perror("calloc fail\n");return;}//计数for (int i = 0; i < n; i++){countA[a[i] - min]++;//映射的下标++就行}//排序int j = 0;for (int i = 0; i < range; i++){while (countA[i]--){a[j++] = i + min;}}free(countA);
}
三.计数排序复杂度分析
📌时间复杂度
计数排序的时间复杂度主要取决于两部分,一是前期遍历数组找出最大值和最小值,这里的时间复杂度为n,二是遍历数组计数,这里的时间复杂度还是n,三是遍历计数数组排序,这里的时间复杂度为range(即max-min),因此我们通常认为,计数排序的时间复杂度为O(n+range);当range接近n时,我们其实可以认为计数排序的时间复杂度为O(n).
📌空间复杂度
计数排序的空间复杂度主要取决于动态开辟的计数数组的大小,即range,因此计数排序的空间复杂度为O(range).
结语
希望这篇计数排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.
有关更多排序相关的知识可以移步:
【数据结构】八大排序算法
https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】八大排序之冒泡排序算法
【数据结构】八大排序之希尔排序算法
【数据结构】八大排序之直接插入排序算法
【数据结构】八大排序之简单选择排序
【数据结构】八大排序之堆排序算法
【数据结构】八大排序之快速排序算法
【数据结构】八大排序算法之归并排序算法
【数据结构】八大排序之计数排序算法
数据结构排序算法篇思维导图:
：ORB算法)
