1.什么是并查集：

对于一个集合S={a1,a2,……an-1,an}，这是可以对集合S进一步划分：S1，S2，……，Sm-1，Sm,我们希望能够快速确定S中的两两元素是否属于S的同一子集；
举个栗子，S={0，1, 2, 3, 4, 5, 6}，如果我们按照一定的规则对集合S进行划分,假设划分后为S1={1, 2, 4}, S2={3, 6}，S3={0, 5}，任意给定两个元素，我们如何确定它们是否属于同一子集？某些合并子集后，又如何确定两两关系？基于此类问题便出现了并查集这种数据结构。
并查集有两个函数操作：
FInd：查找元素所有子集
Union：合并两个子集为一个新的集合；

2、并查集的基本结构

我们可以使用树这种数据结构来表示集合，不同的树就是不同的集合，并查集中包含了多棵树，表示并查集中不同的子集，树的集合是森林，所以并查集属于森林。 若集合S={0, 1, 2, 3, 4, 5, 6}，最初每一个元素都是一棵树。如图：

这里紫色数字的是下标；

union操作：我们只需要将两棵树合并，例如合并0、1、2得到S1={0, 1, 2},合并3和4得到S2={3, 4}

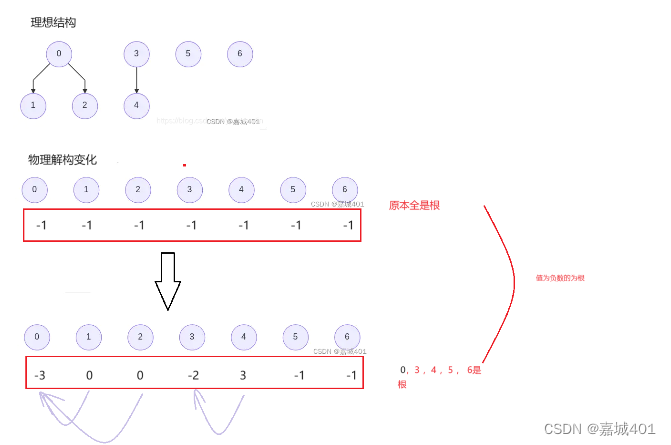
物理结构：
由于 ：1.并查集遵循双亲法：子节点存储父节点的下标；父节点存储该集合的节点个数的负值；

对于Find函数，我们只需要返回该元素所在树的根节点；所以，如果我们想要比较判断1和2是否在一个集合，只需要通过Find(1)和Find(2)返回各自的根节点比较是否相等便可。已知树中的一个节点，找到其根节点的时间复杂度为O(D)，D为节点的深度。

节点之间的关联方法
这里有物理结构可以发现：节点之间的关联方法是：双亲表示法；在子节点内部存父节点的下标；

3.现实问题和代码实现链接

原本并查集会建立一个vector；
这里使用map集合来实现映射；现实中的集合（森林）的元素大概率不是数字，而是文字，所以这里可以使用map集合：map的每个元素可以存两个内容：映射的实现：一个内容填文字，另一个天填数字；
示例：
main.c

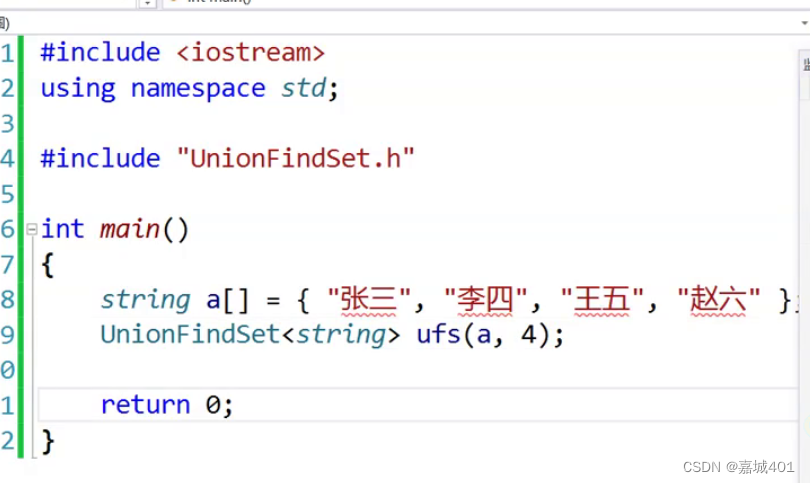
头文件：

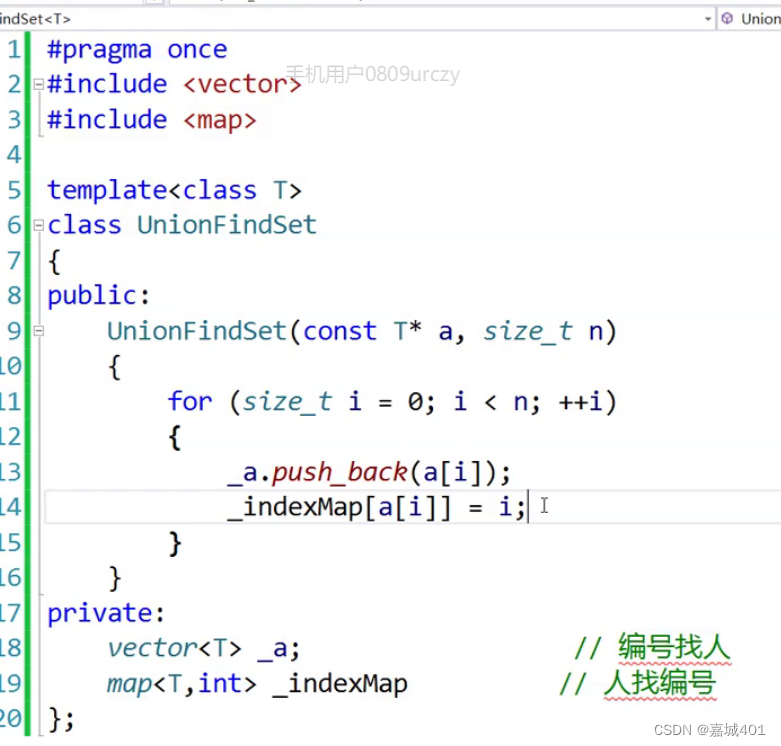
结果：

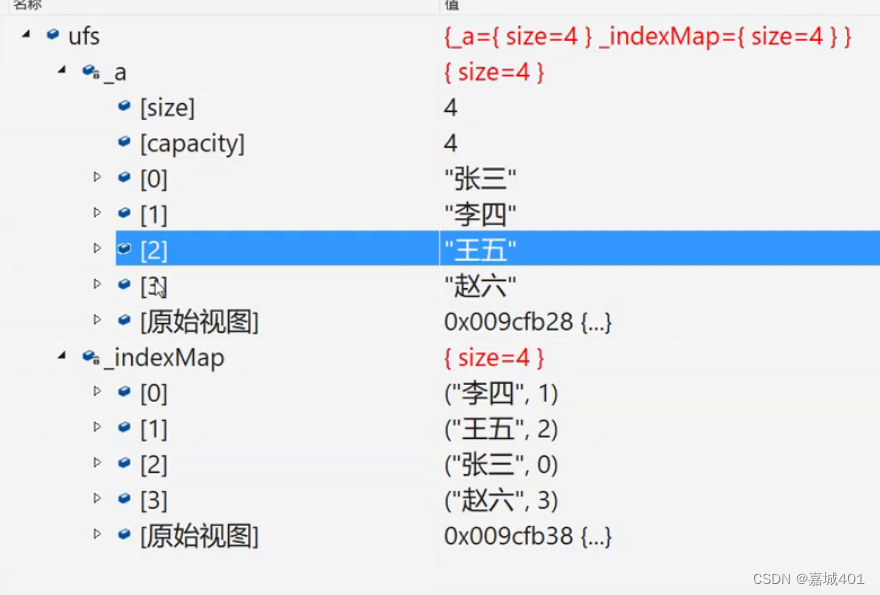
4.代码实现

#pragma once
#include<vector>
using namespace std;
class UnionFindSet
{
public :UnionFindSet(size_t n):_ufs(n , -1){}void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2){return;}if (root1 > root2)swap(root1, root2);_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}int FindRoot(int x){int root = x;while (_ufs[root] >= 0){root = _ufs[root];}return root;}bool IsSet(int x1, int x2){return FindRoot(x1) == FindRoot(x2);}size_t Setsize(){size_t size = 0;for (int i = 0; i < _ufs.size(); i++){if (_ufs[i] < 0){++size;}}return size;}private:vector<int> _ufs;
};