感知机（perceptron）是 二类分类的线性分类模型

• 输入：实例的特征向量
• 输出：实例的类别，取 +1 和 -1 二值
• 感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型
• 旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。
• 感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。
• 预测：对新的输入进行分类

感知机1957年由Rosenblatt（罗森布拉特）提出，是神经网络与支持向量机的基础。

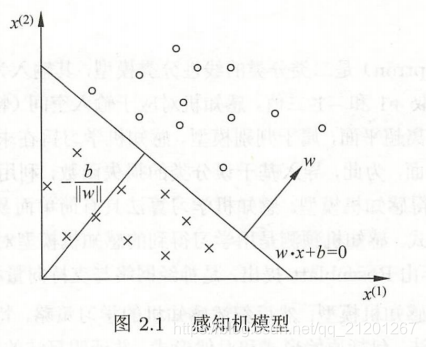
1. 感知机模型

感知机定义：

• 输入空间：$\mathcal{X}\subseteq {\mathbf{R}}^n$
• 输出空间：Y={+1,−1}\mathcal Y = \{+1,-1\}Y={+1,−1}
• $x\in \mathcal{X}$ 特征实例，$y\in \mathcal{Y}$ 表示实例类别
• 输入到输出的函数：$f(x)=sign(\omega \cdot x+b)$
• 参数：$\omega$ 权重向量，$b$ 偏置
• sign 是符号函数：$$sign(x)=\{\begin{array}{r}+1,x\ge 0\\ -1,x<0\end{array}$$
• 感知机是线性分类模型，判别模型
• 几何解释：$\omega \cdot x+b=0$ 对应 n 维空间的一个超平面，$\omega$ 是其法向量，$b$ 为其截距，将点（特征向量）分位正负两类
  

2. 感知机学习策略

• 如果存在一个超平面将所有实例正确的分在平面两侧，称线性可分数据集，否则线性不可分
• 策略：定义损失函数（误分类点到超平面 S 的总距离），并极小化它

---

• 任意一点 $x_0$ 到超平面 $S$ 的距离： $\frac{1}{||\omega |{|}_2}|\omega \cdot x_0+b|$，$||\omega |{|}_2$ 是 $\omega$ 的 $L_2$ 范数

• 所有误分类的点记得集合为 $M$，不考虑分母范数，错误的点 $y_i(\omega \cdot x_i+b)<0$，取距离为正，则感知机的损失函数（经验风险函数）为：
  $$L(\omega ,b)=-\sum _{x_i\in M}{y}_i(\omega \cdot x_i+b)$$

• 选择使上面损失函数最小的模型参数 $\omega ,b$

3. 感知机学习算法

3.1 原始形式

损失函数的最优化问题：随机梯度下降法

• 损失函数的梯度：
  $$\begin{gathered} {\nabla }_{\omega }L(\omega ,b)=-\sum _{x_i\in M}{y}_i{x}_i \\ {\nabla }_{b}L(\omega ,b)=-\sum _{x_i\in M}{y}_i \end{gathered}$$

• 给定 $\eta (0<\eta \le 1)$ 步长（学习率）

• 目标：输出 $\omega ,b$，感知机模型 $f(x)=sign(\omega \cdot x+b)$
  1.选取初值 ${\omega }_0,b_0$
  2.在训练集中选取数据 $(x_i,y_i)$
  3.如果 $y_i(\omega \cdot x_i+b)\le 0$,
  $$\begin{gathered} \omega \leftarrow \omega +\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$
  4.转到2，直到没有误分类点

• 感知机采用不同的初值或选取不同的误分类点，解可以不同

3.2 算法收敛性

算法收敛性证明：（略）

结论：

• 误分类次数 k 有上界，有限次搜索可以找到将训练数据完全正确分开的超平面。
• 当训练数据集线性可分时，感知机学习算法原始形式迭代是收敛的。
• 感知机学习算法存在许多解，既依赖于初值，也依赖于迭代过程中误分类点的选择顺序。为了得到唯一的超平面，需要对分离超平面增加约束条件。这就是第7章将要讲的线性支持向量机的想法。
• 当训练集线性不可分时，感知机学习算法不收敛，迭代结果会发生震荡。

3.3 对偶形式

基本想法：将 $\omega ,b$ 表示成实例 $x_i$ 和标记 $y_i$ 的线性组合形式。

• 经过 n 次修改 $\omega ,b$ ，$\omega ,b$ 关于 $(x_i,y_i)$ 的增量分别是 ${\alpha }_i{y}_i{x}_i,{\alpha }_i{y}_i$，这里 ${\alpha }_i=n_i\eta$

• 最后学到的 $\omega ,b$ 可表示成：
  $$\begin{gathered} \omega =\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ b=\sum _{i=1}^N{\alpha }_i{y}_i \end{gathered}$$

• 当 $\eta =1$ 时，${\alpha }_i$ 表示第 $i$ 个实例点由于误分类进行更新的次数，次数越多，意味着它距离分离超平面越近，很难正确分类，这样的实例对学习结果影响很大

---

目标：求 $\alpha ,b$，感知机模型 $f(x)=sign(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b)$，其中 $\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_N{)}^T$

1. $\alpha =0,b=0$
2. 选取训练集数据 $(x_i,y_i)$
3. 如果 $y_i(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x_i+b)\le 0$
   $$\begin{gathered} {\alpha }_i\leftarrow {\alpha }_i+\eta \\ b\leftarrow b+\eta y_i \end{gathered}$$
   4.转至2，直到没有误分数据

• 对偶形式可以预先将训练集中的实例间的内积计算存储在矩阵中，称为 Gram 矩阵 $\mathbf{G}=[x_i\cdot x_j{]}_{N\times N}$

4. 基于感知机Perceptron的鸢尾花分类实践

请查阅链接