
源 | 机器之心
扩散模型背后的数学可是难倒了一批人。
最近一段时间,AI 作画可谓是火的一塌糊涂。
在你惊叹 AI 绘画能力的同时,可能还不知道的是,扩散模型在其中起了大作用。就拿热门模型 OpenAI 的 DALL·E 2 来说,只需输入简单的文本(prompt),它就可以生成多张 1024*1024 的高清图像。
在 DALL·E 2 公布没多久,谷歌随后发布了 Imagen,这是一个文本到图像的 AI 模型,它能够通过给定的文本描述生成该场景下逼真的图像。
就在前几天,Stability.Ai 公开发布文本生成图像模型 Stable Diffusion 的最新版本,其生成的图像达到商用级别。
自 2020 年谷歌发布 DDPM 以来,扩散模型就逐渐成为生成领域的一个新热点。之后 OpenAI 推出 GLIDE、ADM-G 模型等,都让扩散模型火出圈。
很多研究者认为,基于扩散模型的文本图像生成模型不但参数量小,生成的图像质量却更高,大有要取代 GAN 的势头。
不过,扩散模型背后的数学公式让许多研究者望而却步,众多研究者认为,其比 VAE、GAN 要难理解得多。
近日,来自 Google Research 的研究者撰文《 Understanding Diffusion Models: A Unified Perspective 》,本文以极其详细的方式展示了扩散模型背后的数学原理,目的是让其他研究者可以跟随并了解扩散模型是什么以及它们是如何工作的。

论文地址:
https://arxiv.org/abs/2208.11970
至于这篇论文有多「数学」,论文作者是这样描述的:我们以及其令人痛苦的细节(excruciating detail)展示了这些模型背后的数学。
论文共分为 6 部分,主要包括生成模型;ELBO、VAE 和分级 VAE;变分扩散模型;基于分数的生成模型等。

以下摘取了论文部分内容进行介绍:
 生成模型
生成模型
给定分布中的观察样本 x,生成模型的目标是学习为其真实数据分布 p(x) 进行建模。模型学习完之后,我们就可以生成新的样本。此外,在某些形式下,我们也可以使用学习模型来进行评估观察或对数据进行采样。
当前研究文献中,有几个重要方向,本文只在高层次上简要介绍,主要包括:GAN,其对复杂分布的采样过程进行建模,该过程以对抗方式学习。生成模型,我们也可称之为「基于似然,likelihood-based」的方法,这类模型可以将高似然分配给观察到的数据样本,通常包括自回归、归一化流、VAE。基于能量的建模,在这种方法中,分布被学习为任意灵活的能量函数,然后被归一化。在基于分数的生成模型中,其没有学习对能量函数本身进行建模,而是将基于能量模型的分数学习为神经网络。
在这项研究中,本文探索和回顾了扩散模型,正如文中展示的那样,它们具有基于可能性和基于分数的解释。
 变分扩散模型
变分扩散模型
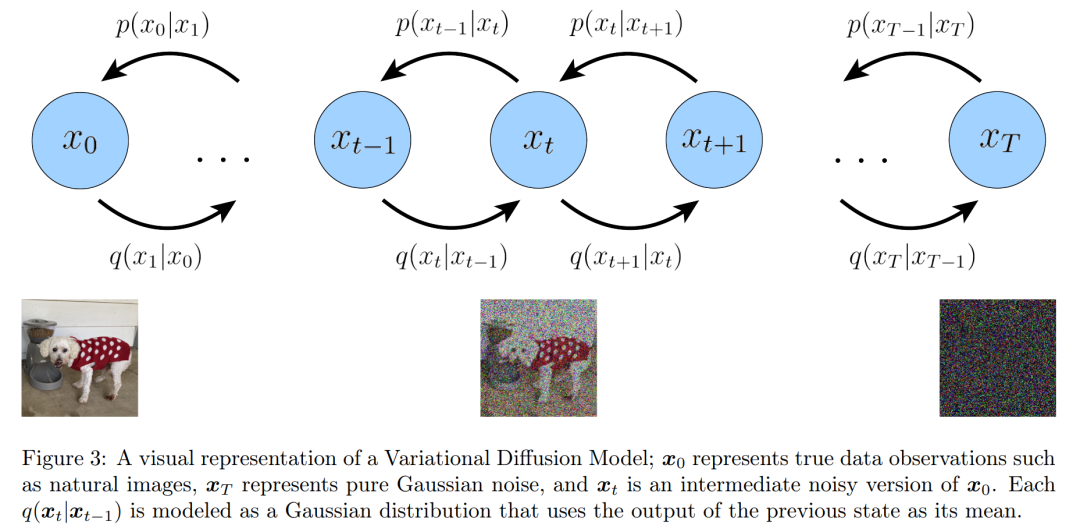
以简单的方式来看,一个变分扩散模型(Variational Diffusion Model, VDM)可以被考虑作为具有三个主要限制(或假设)的马尔可夫分层变分自编码器(MHVAE),它们分别为:
潜在维度完全等同于数据维度;
每个时间步上潜在编码器的结构没有被学到,它被预定义为线性高斯模型。换言之,它是以之前时间步的输出为中心的高斯分布;
潜在编码器的高斯参数随时间变化,过程中最终时间步 T 的潜在分布标是准高斯分布。
此外,研究者明确维护了来自标准马尔可夫分层变分自编码器的分层转换之间的马尔可夫属性。他们对以上三个主要假设的含义一一做了扩展。
从第一个假设开始,由于符号的滥用,现在可以将真实数据样本和潜在变量表示为 x_t,其中 t=0 表示真实样本数据,t ∈ [1, T] 表示相应的潜在变量,它的层级结构由 t 进行索引。VDM 后验与 MHVAE 后验相同,但现在可以重写为如下:

从第二个假设,已知的是编码器中每个潜在变量的分布都是以之前分层潜在变量为中心的高斯分布。与 MHVAE 不同的是,编码器在每个时间步上的结构没有被学到,它被固定为一个线性高斯模型,其中均值和标准差都可以预先设置为超参数或者作为参数学得。在数学上,编码器转换表示为如下:
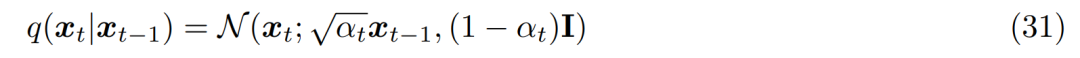
对第三个假设,α_t 根据固定或可学得的 schedule 而随时间演化,使得最终潜在变量 p(x_T) 的分布为标准高斯分布。然后可以更新 MHVAE 的联合分布,将 VDM 的联合分布写为如下:
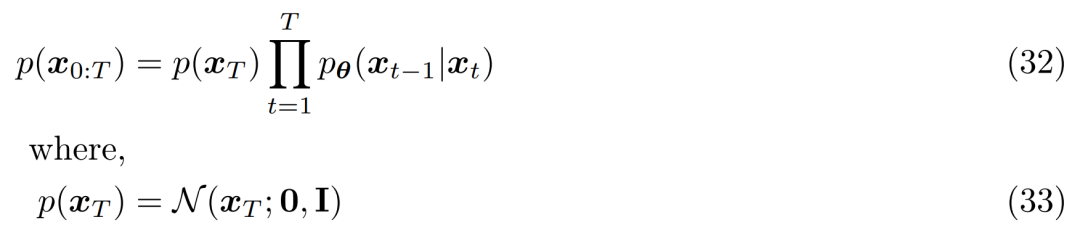
总的来说,这一系列假设描述了一个图像随时间演化的稳定噪声。研究者通过添加高斯噪声渐进地破坏图像,直到最终变得与高斯噪声完全相同。
与任何 HVAE 相似的是,VDM 可以通过最大化证据下界(Evidence Lower Bound, ELBO)来优化,可以推导如下:
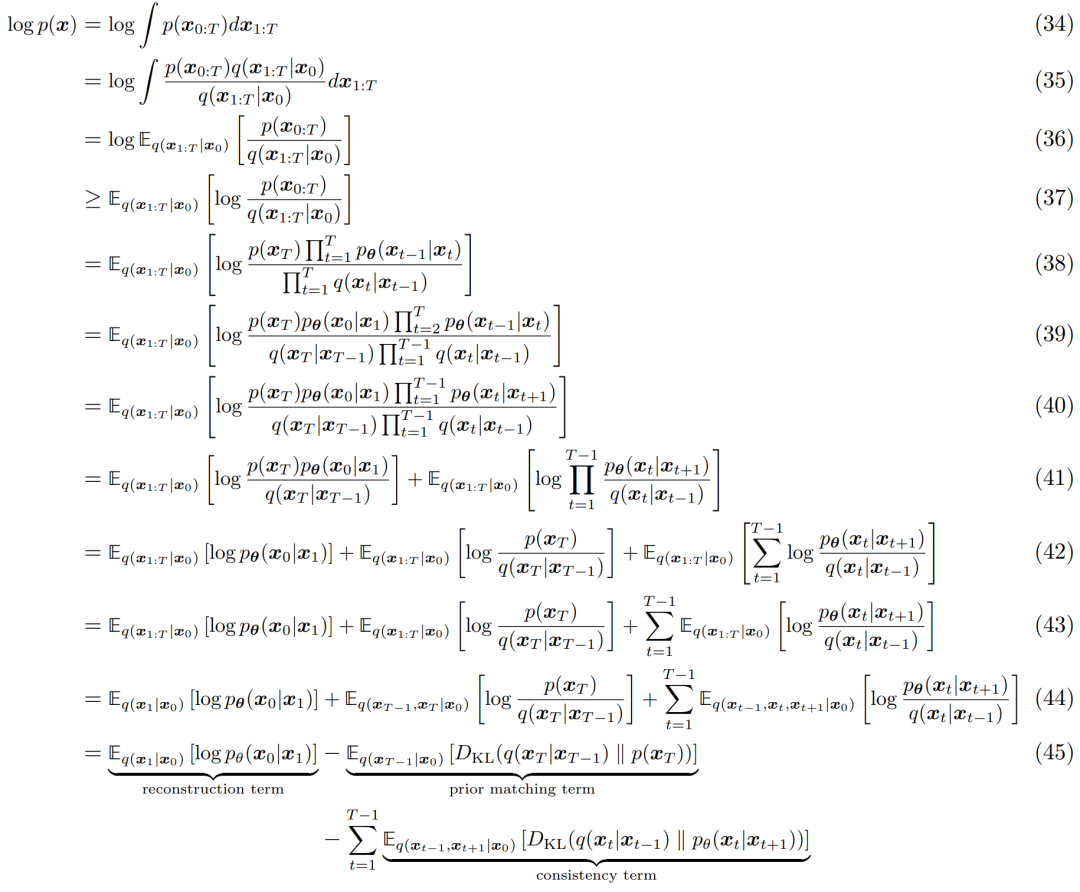
ELBO 的解释过程如下图 4 所示:
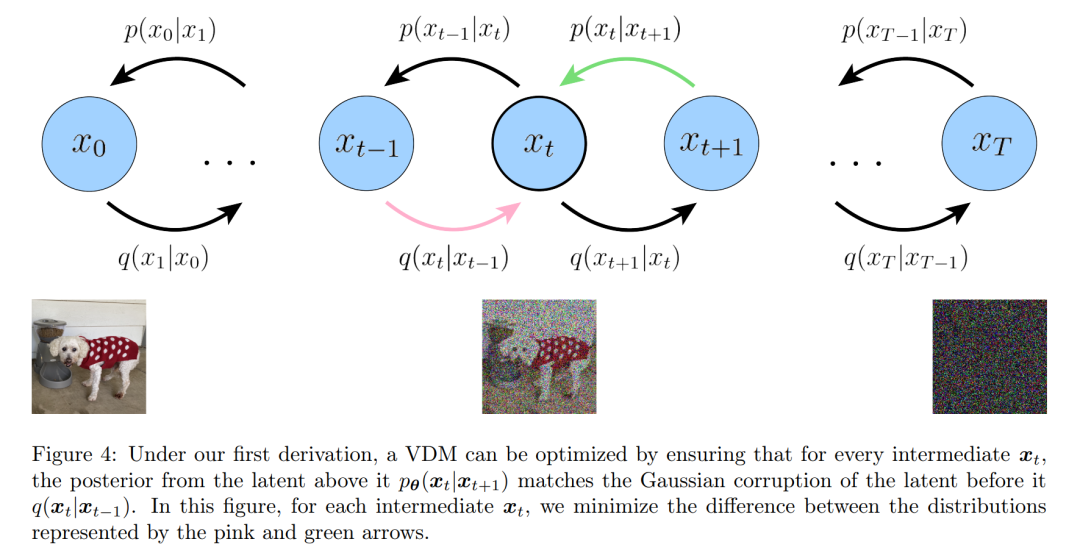
三种等价的解释
正如之前证明的,一个变分扩散模型可以简单地通过学习神经网络来训练,以从任意噪声版本 x_t 及其时间索引 t 中预测原始自然图像 x_0。但是,x_0 有两个等价的参数化,使得可以对 VDM 展开两种进一步的解释。
首先可以利用重参数化技巧。在推导 q(x_t|x_0) 的形式时,文中公式 69 可以被重新排列为如下:

将其带入之前推导出的真实去噪转换均值 µ_q(x_t, x_0),则可以重新推导如下:
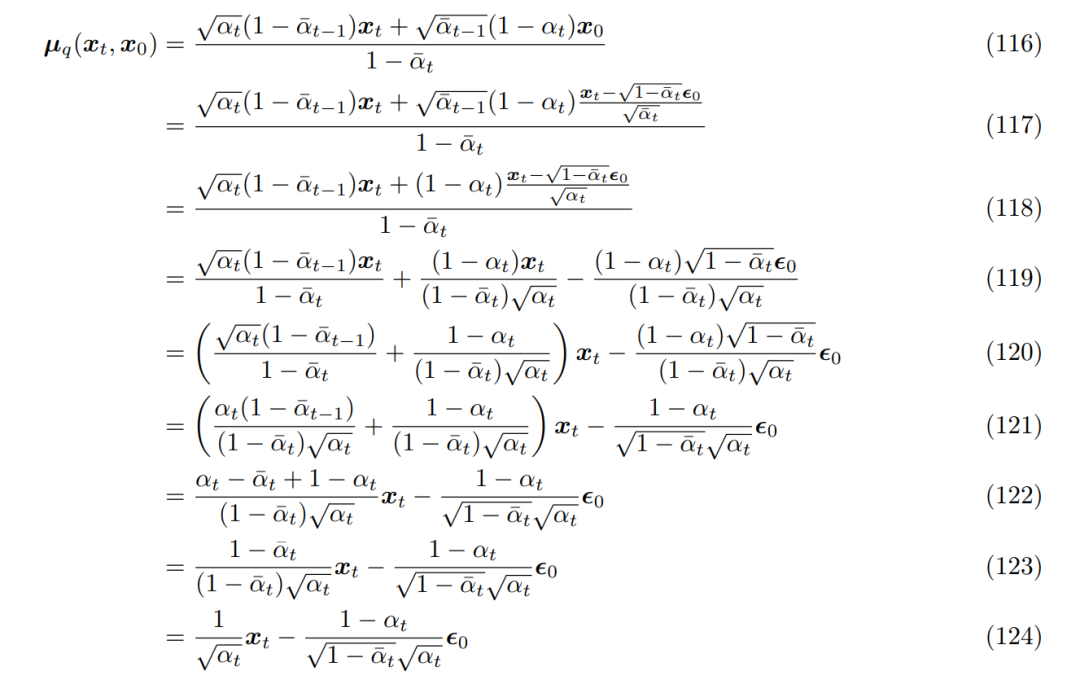
因此可以将近似去噪转换均值 µ_θ(x_t, t) 设置为如下:
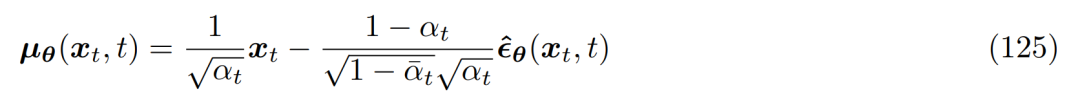
并且相应的优化问题变成如下:
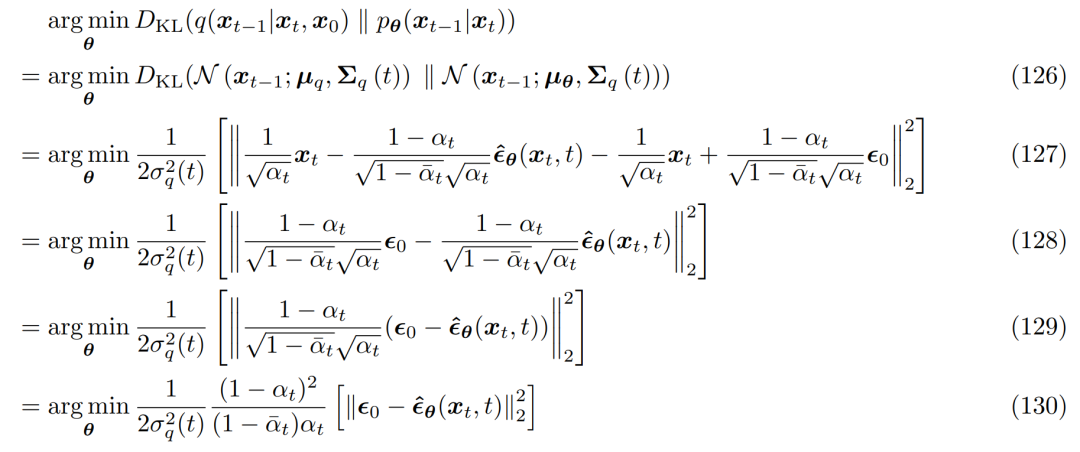
为了推导出变分扩散模型的三种常见解释,需要求助于 Tweedie 公式,它指的是当给定样本时,指数族分布的真实均值可以通过样本的最大似然估计(也称为经验均值)加上一些涉及估计分数的校正项来估计。
从数学上讲,对于一个高斯变量 z ∼ N (z; µ_z, Σ_z),Tweedie 公式表示如下:
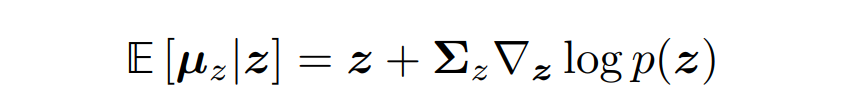
基于分数的生成模型
研究者已经表明,变分扩散模型可以简单地通过优化一个神经网络 s_θ(x_t, t) 来学得,以预测一个得分函数∇ log p(x_t)。但是,推导中的得分项来自 Tweedie 公式的应用。这并不一定为解读得分函数究竟是什么或者它为什么值得建模提供好的直觉或洞见。
好在可以借助另一类生成模型,即基于分数的生成模型,来获得这种直觉。研究者的确证明了之前推导出的 VDM 公式具有等价的基于分数的生成建模公式,使得可以在这两种解释之间灵活切换。
为了理解为什么优化一个得分函数是有意义的,研究者重新审视了基于能量的模型。任意灵活的概率分布可以写成如下形式:

避免计算或建模归一化常数的一种方式是使用神经网络 s_θ(x) 来学习分布 p(x) 的得分函数∇ log p(x)。这是观察到了公式 152 两边可以进行对数求导:
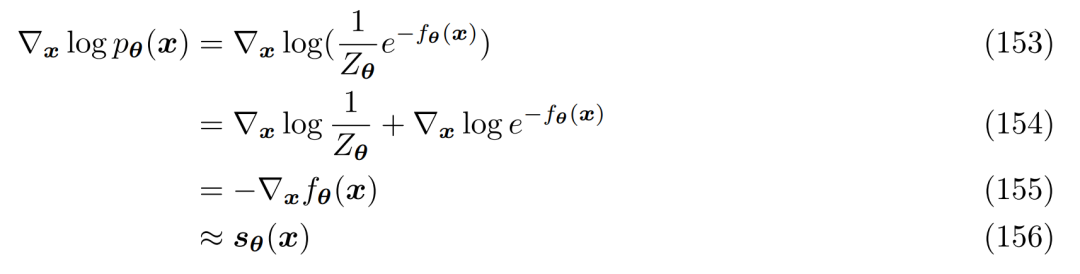
它可以自由地表示为神经网络,不涉及任何归一化常数。通过利用真值得分函数最小化 Fisher 散度,可以优化得分函数。

直观地讲,得分函数在数据 x 所在的整个空间上定义了一个向量场,并指向模型,具体如下图 6 所示。
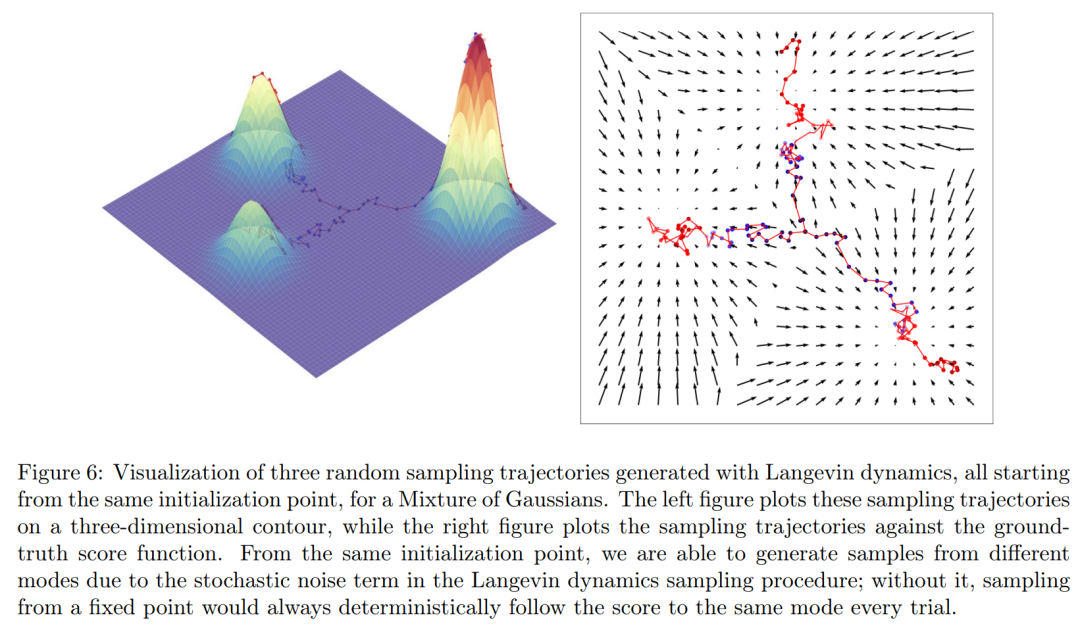
最终,研究者从训练目标和抽样过程两方面,建立了变分扩散模型和基于分数的生成模型之间的显式关联。
更多细节内容请参阅原论文。
后台回复关键词【入群】
加入卖萌屋NLP、CV、搜推广与求职讨论群
)


)



)



)




)


