1 引言
傅里叶级数 (Fourier Series, FS) 是《高等数学》中遇到的一个重要的级数,它可以将任意一个满足狄利克雷条件的函数为一系列三角级数的和。最早由法国数学家傅里叶在研究偏微分方程的边值问题时提出,极大地推动了偏微分方程理论的发展。根据欧拉公式及其推导式,傅里叶级数又可以推导出《信号与系统》中最重要的傅里叶变换(Fourier Transform, FT)。FT由于可以将信号从时域到频域来回变换,分析信号的成分,从而广泛应用于信号处理领域。在计算机处理中,信号被离散化为采样点,针对离散采样点的傅里叶变换成为了《数字信号处理》中的离散傅里叶变换(Discrete Fourier Transform, DFT)。但是由于DFT计算量过于庞大(计算复杂度高),1965年由J.W.库利和T.W.图基提出了最早版本的快速傅里叶变换(Fast Fourier Transform, FFT),将计算量减少了几个量级,从而使得计算机更加快速地处理信号,从而促进通信、信号处理领域的快速发展。近年来由于量子计算机的兴起,量子傅里叶变换(Quantum Fourier Transform, QFT)更是可以对FFT进行指数级别的加速。
由于这一系列变换出现在不同学科中,老师在讲课时也是各自独立讲解,所以大多数同学(包括我)对其中的似曾相识的公式,一直分不清有什么区别和联系,这篇文章着重于这一系列傅里叶算法的直接的相互推导。
2 一维傅里叶级数(FS)
2.1 周期性
首先写出傅里叶级数的表达式:
其中,
即可被分解为N阶的FS。
由于
当
2.2 正交性
何为正交?正交是线性代数中的概念,即列向量a, b的内积为0,就称这两向量正交。正交还可以不严谨地理解为这两组向量之间没有关系。
同样地,借鉴这个定义,在连续函数中的正交为:
此时,我们令
积分是一个线性算符,积分和等于和的积分,上式可以看做两个三角函数分别积分。当
当
前一项,积分明显为0,后一项为
同理,还可以尝试令
2.3 求系数
首先看
就是把要分解的函数和傅里叶级数同时做了积分,等号右边可以拆为2N+1个积分和,根据前面的周期性可知,除了第一项以外,后面的项的积分均为0。故上式可以化简为:
这里的表达式就说明了
接着,我们尝试求
其中,
利用上面证明的周期性和正交性,我们可以知道,只有当
故:
同理,我们可以得到正弦分量的系数。最后结果为:
到这里,所有FS的系数就能求出来了。但是这里有个比较诡异的地方,当
3 傅里叶变换(FT)
3.1 FT和FS之间的关系
首先,把傅里叶变换的公式写出来:
然后,回到傅里叶级数。
根据欧拉公式
及其一个简单的变形:
代入到傅里叶级数中:
令
傅里叶级数变为:
变换后的系数
若
所以,
当
由于
令
3.2离散傅里叶变换
在计算机中,我们不可能令
因此我们就得到了能够被计算机执行的离散傅里叶变换的函数式。
为便于理解,先带个具体数据进去考虑。若采样的数据点为8,频率分量个数也为8。用
来表示这种情况下的DFT函数。
上面这些式子用矩阵表示为,假设有个矩阵

将上面的一组求和式翻译成矩阵
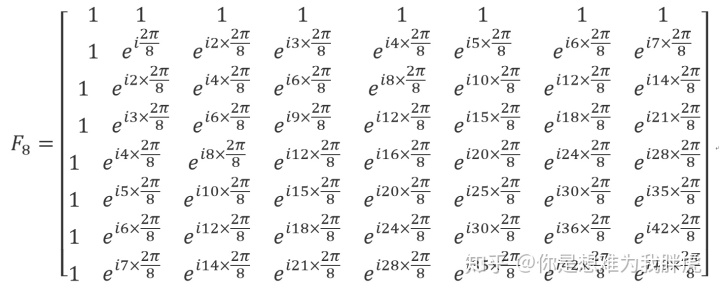
为了便于观察,令

根据

3.3 快速傅里叶变换
从3.2节,我们知道了,要完成一次DFS需要用一个矩阵去乘以一个时域组成的列向量,而这个矩阵大小与时域上的采样点和频域分量的个数有关。若它们的个数为
仍然以

而

同样地,我们还可以写出
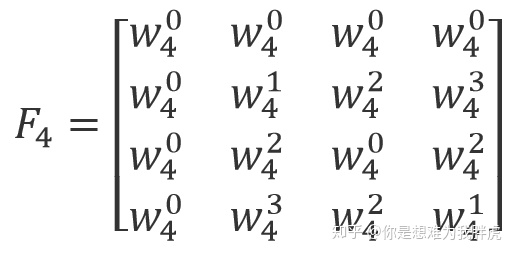
同样地,令
值得注意的是
故
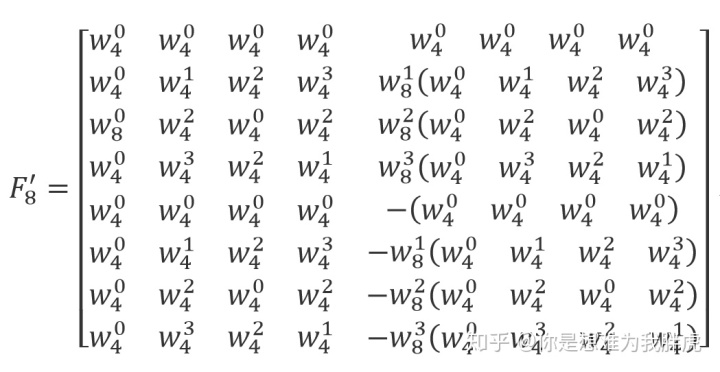
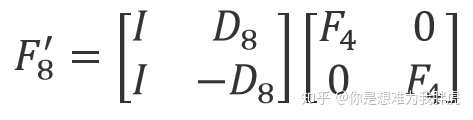
其中

最后
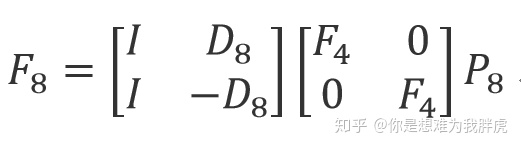
这样一来上面这个矩阵需要多少次乘法呢?由于
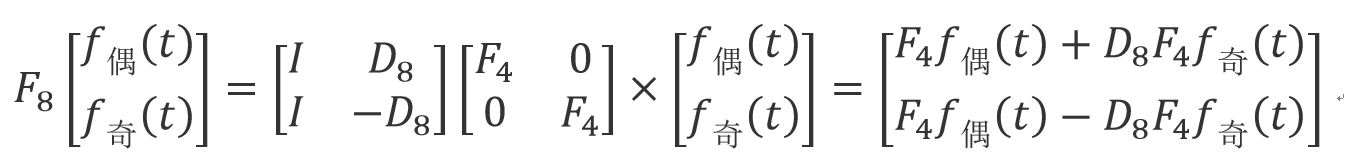
显然,主要的计算量在于
同理,我们还可以对
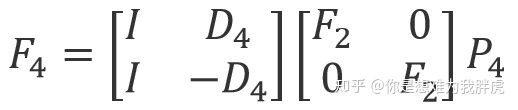
带入
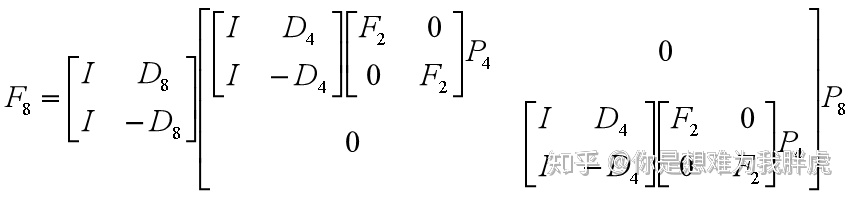
化简下:
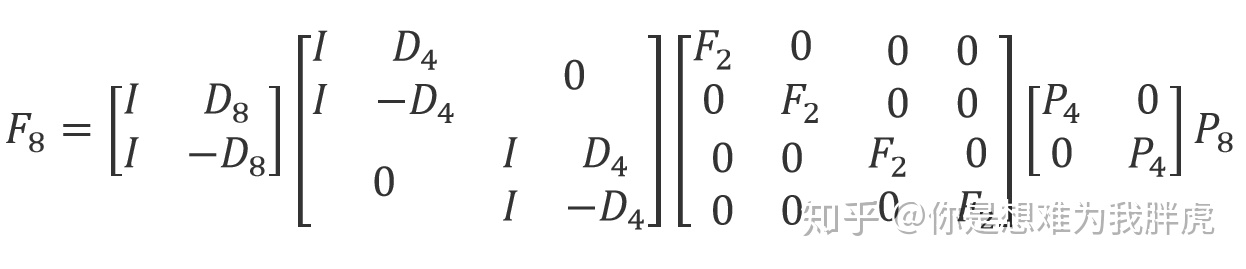
此时需要的乘法数量为
推广到更一般的情况,仍然可以使用类似上述的递归方式,最后FFT的计算复杂度变为
4、量子傅里叶变换
如果对量子逻辑门有一定了解的同学,看到上面最终的递归化简式,已经发现和量子逻辑门很像了。比如我们看

那这不就是
再比如
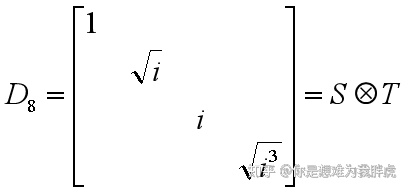
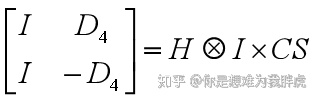
其中
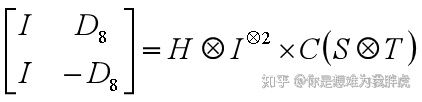
其中,
接着 我们观察置换矩阵
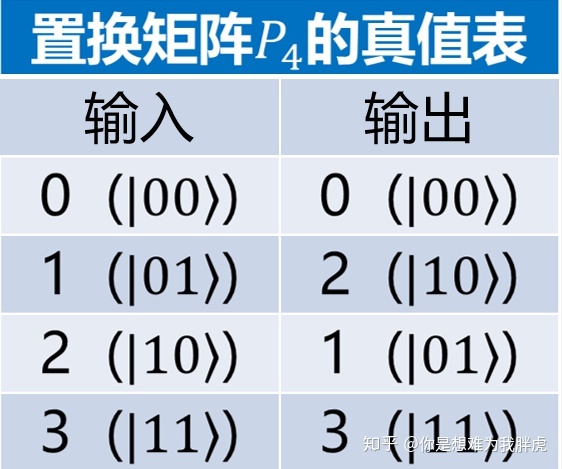
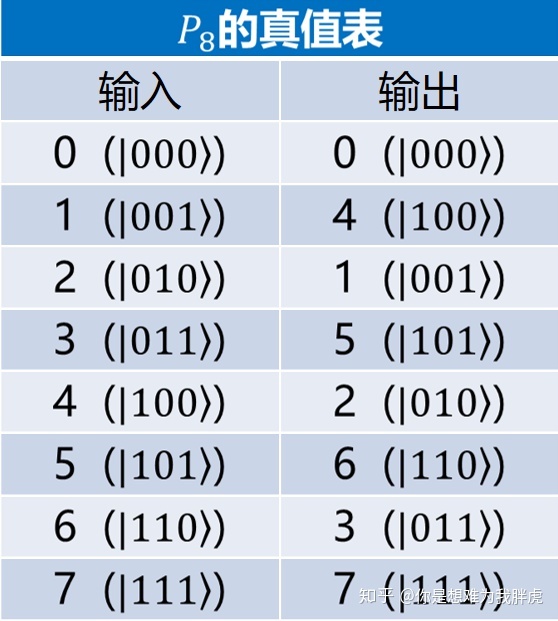
不难发现
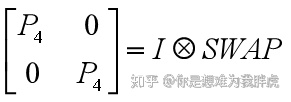
根据
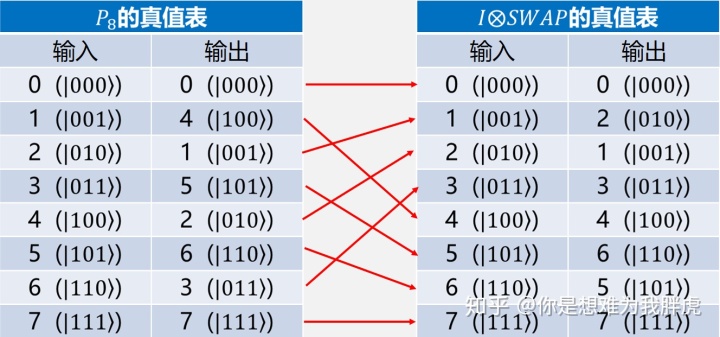
列出合并后的真值表,那这不就是1,3 qubit交换位置嘛。
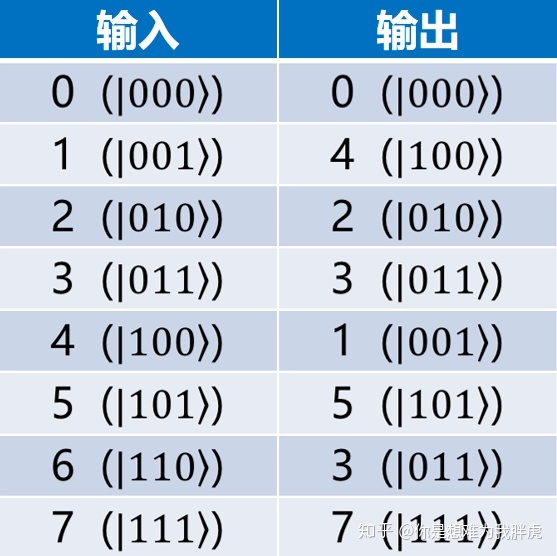
即:
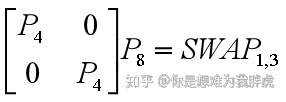
整个
量子电路如下:
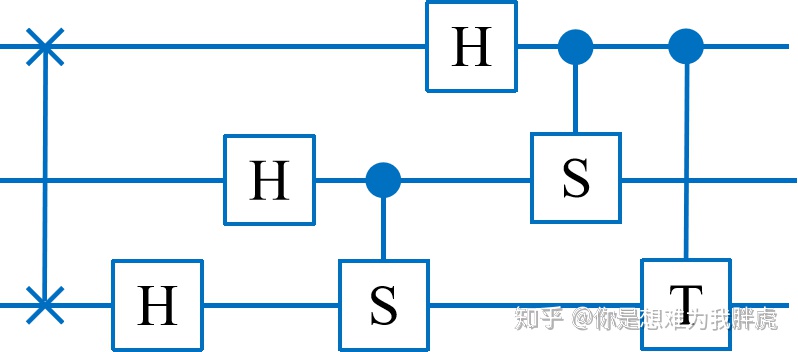
有兴趣的可以对比一下与《量子计算与量子信息》书中盒子5.1是否是等价的电路。如果以基本量子门作为计算单元的话,QFT的复杂度则只需

)
 上)



)


![nodejs 获取cpu核心数量_用 NodeJS 充分利用多核 CPU 的资源[每日前端夜话0xCB]](http://pic.xiahunao.cn/nodejs 获取cpu核心数量_用 NodeJS 充分利用多核 CPU 的资源[每日前端夜话0xCB])
)


)
算法及其推广)


用法及代码示例)

)